11. Popište rozklad chyby na nedoučení a přeučení (Bias Variance Decomposition of Error) a uveďte jaké složky typicky redukuje bagging a boosting a proč.
Bias-Variance Decomposition of Error¶
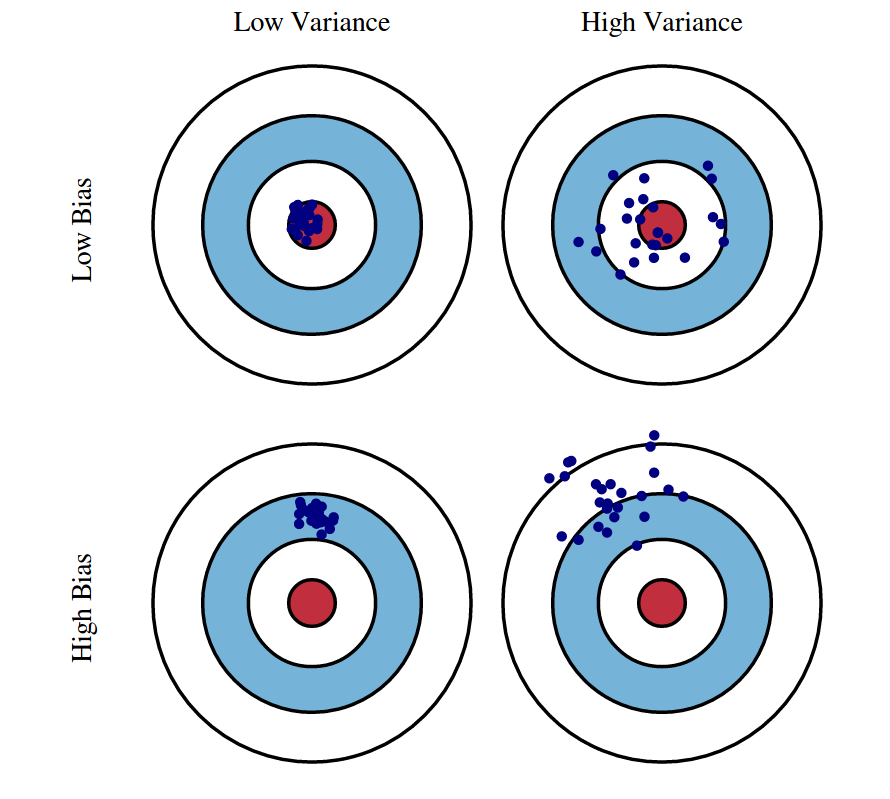
The Bias-Variance decomposition analyzes a learning algorithm's expected generalization error for a specific problem. The algorithm's generalization error can be divided into three components: bias, variance, and irreducible error.
The expected prediction error for a particular point x can be broken down as follows:
E[y - \hat{f}^2] = Bias^2[\hat{f}] + Var[\hat{f}] + \sigma^2
In this formula: - E[y - \hat{f}^2] represents the expected prediction error - Bias^2[\hat{f}] represents the squared bias - Var[\hat{f}] symbolizes the variance - \sigma^2 denotes the irreducible error
Bias¶
The bias of an estimator is the difference between this estimator's expected value and the true value of the parameter being estimated. High bias may lead an algorithm to overlook the significant relationships between features and target outputs, a phenomenon called underfitting.
Variance¶
Variance reflects the degree to which the estimate of the target function would vary if different training data was used. High variance can lead an algorithm to model the random noise in the training data, rather than the intended outputs, a situation known as overfitting.
Var[\hat{f}] = E[\hat{f}^2] - E^2[\hat{f}]
Irreducible Error¶
The irreducible error originates from noise intrinsic to the problem itself. No matter the algorithm used, this part of the error cannot be reduced.
Bagging and Boosting¶
Bagging and boosting are two ensemble methods that aim to form a robust classifier from a set of weaker ones.
Bagging¶
Bagging, which stands for Bootstrap Aggregating, helps reduce variance through a technique known as bootstrapping. This technique involves creating multiple subsets of the original data, with replacement, and then training a separate model on each subset. By averaging the prediction of each model for a given input, bagging reduces the effect of 'noise' or variance errors. Since each model in the ensemble votes with equal weight, the aggregate opinion should be a more robust prediction than any single model. Therefore, the high variance is reduced.
Boosting¶
Boosting operates differently. It's a sequential process where each subsequent model attempts to correct the errors of the previous model. The models learn from each other, effectively reducing bias. At first, an initial model is built on the data, which may lead to some bias (misclassification of data points). Then, the next model focuses on the data points which were misclassified by the previous model, trying to correct them. Therefore, each model is trained to be an expert on the data points that are particularly difficult to predict, gradually reducing the bias.
Boosting also addresses variance to some extent by combining several weak learners. The idea here is that by forming a committee of weak learners (models that do only slightly better than random chance), the ensemble model (the boosting model) will be a strong learner, or a model that is correctly tuned to the structure and complexities in the data. Each of the individual models can have high variance, but the ensemble's decision-making process can help to alleviate overfitting.
Key Takeaways¶
-
Bias-Variance Tradeoff: Bias stems from the simplifying assumptions made by the model about the data, while variance indicates how much the prediction would vary if we used a different training dataset. Striking the right balance between bias and variance is essential to crafting an accurate model.
-
Bagging: Bagging decreases variance by training multiple models on various subsets of the data and averaging their predictions. It is beneficial when the model is complex and exhibits high variance.
-
Boosting: Boosting minimizes bias by training numerous weak learners and amalgamating them into a robust learner. It is valuable when the model is overly simple and suffers from high bias.
-
To achieve an optimal machine learning model, aim for low bias and low variance. Bagging and Boosting are two influential ensemble methods that aid in attaining this balance.