4. Neuronové sítě

Definice¶

Neuronové sítě se skládají z vrstev neuronů, které jsou propojené spolu. Každý neuron má několik vstupů a jeden výstup. Když je neuron aktivován, přenáší informaci z vstupů na výstup. Vrstvy neuronů jsou propojené tak, že výstupy jedné vrstvy jsou vstupy pro další vrstvu. Neuronové sítě jsou učeny tak, že se na jejich vstupy aplikují různé vstupy a příslušné výstupy, a pomocí algoritmů se pak váhy mezi jednotlivými neurony upravují tak, aby byl výstup co nejpřesnější.

Použiti¶

Neuronové sítě jsou velmi účinné pro řešení složitých problémů, protože dokážou zpracovat velké množství dat a najít vztahy mezi nimi, které by byly pro člověka obtížné zjistit. Jsou používány v mnoha oblastech, jako je například počítačové vidění, překlad nebo hledání řešení v herních situacích. Neuronové sítě jsou také často používány v robotice pro řízení pohybu robotů nebo pro řešení jiných složitých problémů

Otázky¶

Jak funguje perceptonový algoritmus?¶

Perceptron¶

Nejjednodušší neuronová sít, slouží jako binární klasifikátor.
Mapuje vstupní vektor na výstup pomocí lineární kombinace.
Skládá se z jednoho neuronu, který vypočte lineární kombinaci vstupů a vah, přičte bias a tuto hodnotu vnitřního potenciálu prožene nelineární aktivační funkcí, jejíž výstup je zároveň výstupem celého perceptronu.
Aktivační funkce bývá často step function,, která je 1 pro vnitřní potenciál >= 0 jinak 0.
Perceptron nelze použít pro problémy, které nejsou lineárně separabilní (např. XOR).

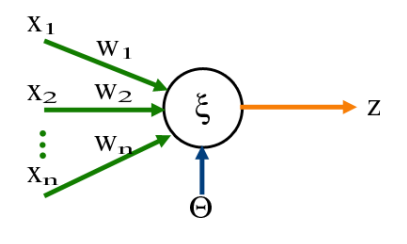
Perceptron algoritmus¶

Váhový vektor $w_0$ je náhodně vygenerovaný
Opakovaně se vybírá náhodný prvek z trénovacích dat
1. Je-li z třídy $P$ ale hodnota $w_x$ je záporná, pak se nový vektor vah vypočte přičtením vektoru $x$ k vektoru vah $w$ , čímž se $x$ posune do pozitivní nadroviny určené vektorem vah.
2. Pokud je z třídy $N$ a hodnota $w_x$ je kladná, tak se $x$ od $w$ odečte, čímž se bod posune do negativní poloroviny.
Tyto operace postupně posouvají vektor vah k optimálnímu rozdělení tříd.
Jako prvotní nastavení vah lze zvolit průměr všech kladných vektorů a odečíst průměr všech záporných.

Gradient learning¶

Na rozdíl od perceptronového algoritmu konverguje i pro lineárně nesaparabilní data a maximalizuje rozdělení tříd.
Určíme ztrátovou funkci např. pomocí sum of squared errors.
Funkce je minimalizována krokem proti směru gradientu, který je ovládán ještě parametrem learning rate.
K výpočtu gradientu je potřeba spočítat parciální derivaci ztrátové funkce vůči každé váze vektoru w.

Co to je cross entropy loss?¶

Ztrátová funkce používaná pro klasifikaci tříd.
Cross-entropy loss se počítá jako průměr logaritmické ztráty mezi skutečnou hodnotou a předpovězenou hodnotou pro každou kategorii. Ztráta se počítá tak, že se z skutečné hodnoty odečte předpovězená hodnota a výsledek se zapíše do logaritmické funkce. Výsledná hodnota je potom vynásobena opačným znaménkem, aby se dostala kladná hodnota.
Hodnota funkce stoupá tím více, čím jistější si je model klasifikací špatné třídy. Nejvíce tedy trestá predikce, kterými si je model jistý a jsou špatné.

Jak napočítám chybu pro zpětné šíření u neuronu ve skryté vrstvě?¶

MLP - Multilayer perceptron¶

Mají více vrstev s více neurony, přičemž výstup každého neuronu vede do každého neuronu nadcházející vrstvy.
Všechny neurony mají nelineární aktivační funkci (často sigmoida, tanh, ReLU,...), která musí být diferencovatelná.
MLP jsou schopny fungovat i na data co nejsou lineárně separabilní. Neuronová sít se vstupní vrstvou, jednou skrytou vrstvou a výstupní vrstvou může reprezentovat libovolnou spojitou funkci.
Každá vrstva MLP je nějaká funkce a celá NN je jejich kompozice, tedy složená funkce. Abychom mohli použít gradientní sestup pro učení vah, musíme najít parciální derivaci ztrátové funkci vůči každé váze (tedy i ty v dřívějších vrstvách).
- Ty vypočítáme pomocí tzv. chain rule pro derivace složených funkcí.
- $\frac{\delta f}{\delta x} = \frac{\delta f}{\delta q} \frac{\delta q}{\delta x}$

Backpropagace - zpětné šíření chyby¶

Pro všechna trénovací data necháme spočítat výstup sítě a pak vyčíslíme hodnotu cost funkce jako například průměrnou hodnotu cross-entropy.
Postupně od poslední vrstvy směrem ke vstupní počítáme parciální derivace jednotlivých vah vůči cost funkci, čímž získáme gradient.
Pak provedeme gradientní sestup regulovaný learning ratem a toto opakujeme dokud není splněné terminální kritérium.

Co je momentum?¶

Je to způsob, jak zlepšit rychlost a účinnost trénování neuronové sítě tím, že se váhy jednotlivých neuronů upravují s využitím momentu předchozích změn vah.
To znamená, že pokud váha neuronu byla v minulosti úspěšně změněna o určitou hodnotu, je pravděpodobné, že by měla být změněna o podobnou hodnotu i v budoucnu. To může pomoci zvýšit rychlost a účinnost trénování neuronové sítě, protože se váhy jednotlivých neuronů budou měnit směrem, který v minulosti prokázal úspěch.

Jak zhruba funguje ADAM?¶

ADAM (adaptive moment estimation)
Optimalizátor, který využívá gradient decsent jakožto momentum a také adaptivní learning rate parametry pro jednotlivé váhy.
Výhodou toho je, že váhy které způsobily velké oscilace v jednom kroku mohou být penalizovány v dalším kroku, aby se zamezilo jejich přeučení.

Jak se učí SOM?¶

Kohonen’s self-organizing maps (SOM)¶

Typ neuronové site trénované nesupervizovanym učením.
Vytváří nízkorozměrné (obvykle dvourozměrné), diskrétní mapy.
Mapy využívají neighbourhood funkci, která se snaží zachovat topologické vlastnosti prostoru.
Algoritmus:
1. Váhy neuronů jsou inicializovány na malé hodnoty
2. Je vybrán nějaký vstup a vybere se neuron, který leží nejblíže (např. euklidovsky) k danému vstupu
3. Neuron spolu s jeho okolím jsou updatovány a posunuty směrem ke vstupu
4. Toto se opakuje a neurony (váhy neuronů) se tak posouvají směrem k datovým bodům dokud nejsou rozprostřeny tak, že zachycují nějakou jejich strukturu. Váhy neuronů pak lze použít pro popis dané oblasti které náleží aniž bychom potřebovali spoustu dat, co tam původně byla