Zpracovani-obrazu #Transformace-obrazu #Filtrace #Gradientni-metody #Detekce-hran #Fourierova-transformace

Zpracovaní obrazu

• Obrázek je většinou reprezentován maticí, kde daný pixel je na pozici $(i, j)$, jeho hodnota je $f(i, j)$
• Reprezentace obrazu
  • Nejčastěji jas (úrovně šedi)
  • Fourierova transformace
• Částečné úkoly rozpoznávání
  • Zachycení obrázku a digitalizace
  • Preprocessing
  • Segmentace pozadí a objektů
  • Popis objektů
  • Pochopení obsahu
• Reprezentace obrazových informací - úrovně
  1. Matice čísel - jas, grayscale...
  2. Segmentovaný obraz (hrany a plochy)
  3. Geometrická reprezentace (znalost 2/3D hran a okolních vlivů - světla atd.)
  4. Vztahové modely, sémantické sítě, derivace

Preprocessing

• Úkol
  • Potlačení šumu
  • Odstranění geometrických zkreslení
  • Potlačit/zvýraznit sledované featury obrazu

Grayscale transformace

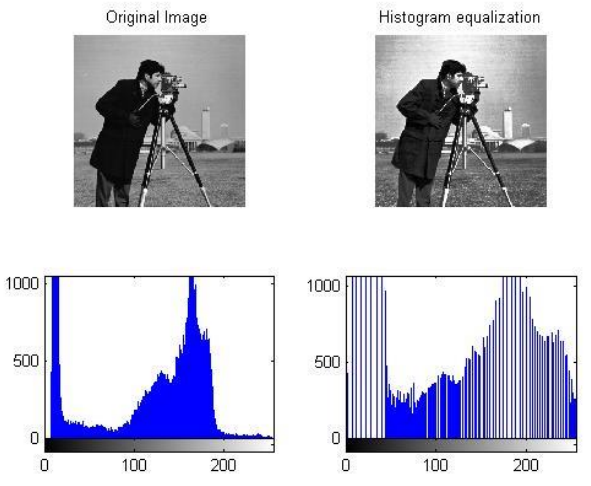
• Slouží k vyrovnání histogramu (histogram equalization)
  • Stejná frekvence všech stupňů šedi
  • Vylepšení vlastnosti obrazu pro vizuální pozorovaní
• Používá se k zvýšení kontrastu

Geometrická transformace

• Slouží ke korekci zkreslení zařízením
• Akce
  • Přiblížení
  • Otáčení
  • Posouvání
  • transformace
• Geometrická ( prostorová ) transformace
  • Pokud je známá, aplikujeme inverzní matici
  • Jinak hledáme odpovídající ( correspondence ) body a na jejich základě odhadujeme transformaci
  • Transformace se často aproximuje pomoci polynomu řádu $m$
  • Polynomiální rovnice
    • $x'=\sum_{r=0}^m\sum_{k=0}^{m-r}a_{rk}x^ry^k$
    • $y'=\sum_{r=0}^m\sum_{k=0}^{m-r}b_{rk}x^ry^k$
  • Na základě komplexity se vybere transformační funkce
    • Bilinear transformation
      • $x'=a_0+a_1x+a_2y+a_3xy$
      • $y'=b_0+b_1x+b_2y+b_3xy$
    • Affine transformation
      • $x'=a_0+a_1x+a_2y$
      • $y'=b_0+b_1x+b_2y$
  • Řešení je nalezeno metodou nejmenších čtverců (LSM)
  • Po transformaci je nutná grayscale korekce

Filtrace

• K potlačení nechtěných jasných komponent
• Transformuje stupně jasu
• Ve frekvenční doméně (2D Fourierova transformace)
• V prostorové doméně (2D konvoluce, aplikace konvoluční kernel matice)
• Filtrace podle průměru
  • Rozmazává hrany
• Mediánová filtrace
  • Zachovává hrany
    • Občas ale vytváří nové hrany
  • Slouží k odstranění impulzivního šumu

Gradientní metody

• Hledaní ostrých hran
• Zapříčiňuje lepší detekci
• Populární gradientní operátory
  • Roberts’ operator
    • Aproximace 1. parciální derivace
  • Sobel's operator
    • Aproximace 1. parciální derivace
    • Přesnější než Roberts’ operator
  • Laplace's operator
    • Aproximace 2. parciální derivace
    • Způsobuje duplikaci hran

Detekce hran

LoG filter

• Dobře aproximuje biologickou detekci hran
• Vyhlazeni
  1. Gaussovský filtr
  2. Laplaceho filtr
• Hledaní hran

Canny detector

• Požadavky
  • Low error rate (nalezení jen a pouze hran)
  • Minimalizace vzdáleností hran obrázku a detekovaných hran
  • Reprezentace hrany jednou vrstvou pixelů
• Postup
  1. Nejdříve vyhladí obrázek Gaussovským filtrem
  2. Edge filtr se použije s rozlišením směru
  3. Použije se Hysteresis thresholding
     1. Pokud je pixel nad horním prahem, je to hrana
     2. Pokud je mezi prahy a je vedle hraničního pixelu, je to hrana taky

Fourierova transformace

• Slouží k určení množiny harmonických funkcí, ze kterých se funkce skládá.
  • Neboli snaží se rozložit obrázek na součet sinusových vln
• Proměnné
  • Amplituda
  • Frekvence
  • Posunuti
• Výsledek
  • Amplitude spectrum
    • Graf zachycující amplitudu ku frekvenci
  • Phase spectrum
    • Graf zachycující fázový posun ku frekvenci
• Vlastnosti
  • Linearita výhodné pro filtraci šumu
  • Konvoluce výhodné pro lineární filtraci
  • Posun (spektrum se posouvá do středu, při násobení $(-1)^{x+y}$
• Fast Fourierova transformace
  • Efektivní implementace Fourierovy transformace
  • Funguje na principu rekurzivním rozdelovanim dat
• Pokud existuje hrana tak se zobrazí jako kolmice na danou hranu
  •