Feature-selection #Redukce-dimenzionality¶
Redukce dimenzionality¶
- Cílem je vybrat ty hodnoty, které nesou největší informační hodnotu
- Zjednodušení dat vede k zrychlení modelu, snížení dimenzionality
- Snaha o nalezení ideální podmnožiny dat, která data zredukuje, ale zachová (případně i zlepší) celkovou informaci, kterou se snažíme z dat získat
Feature selection¶
Snaha odpovědět na otázku: Jak moc je příznak X_i relevantní pro predikování Y Dva přístupy při vytváření podmnožiny dat: - Univariate method - Considers one variable (feature) at a time. - Multivariate method - Considers subsets of variables (features) together.
Metody¶
- Filter method
- Hodnotí příznaky nezávisle na zvoleném predikčním modelu/klasifikátoru
- 3 kroky
- Měření relevance příznaku
- Seřazení příznaků dle relevance
- Použití statistických testů k výběru
- Odolné proti přeučení
- Nemusí úspěšně najít některé důležité příznaky
- Wrapper method
- Používá klasifikátor a na základě jeho výsledků upravuje vybranou podmnožinu
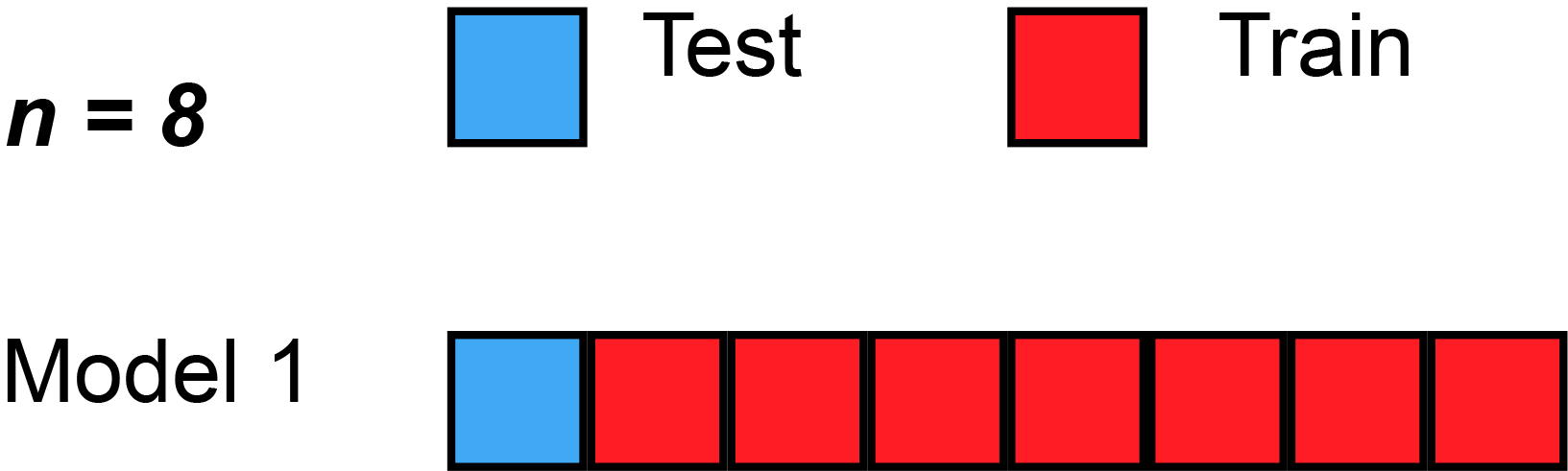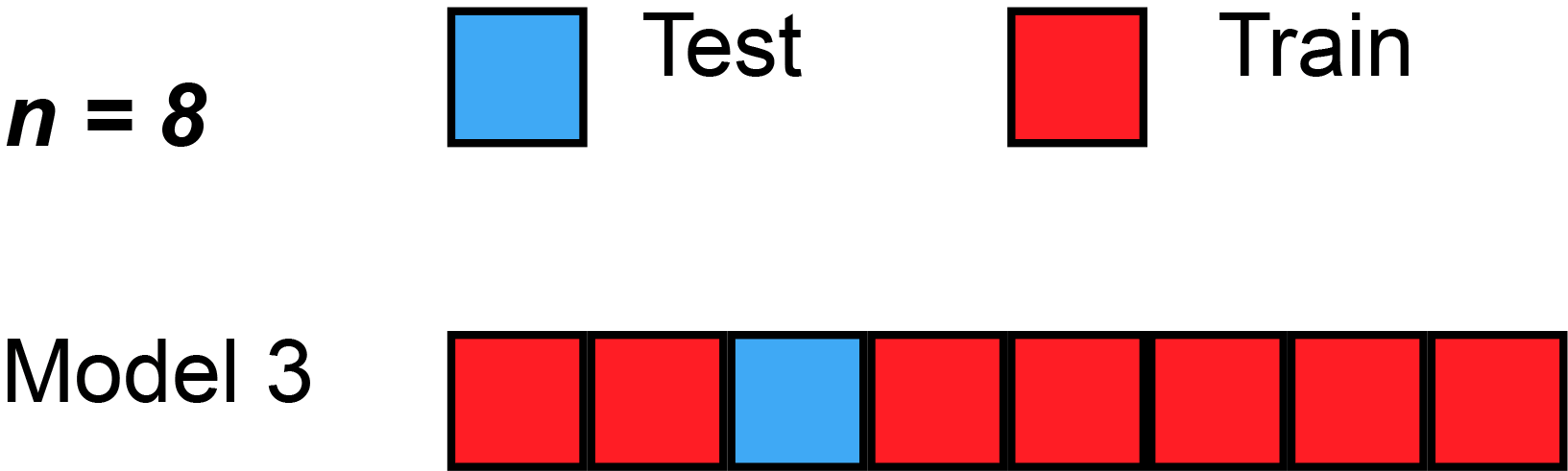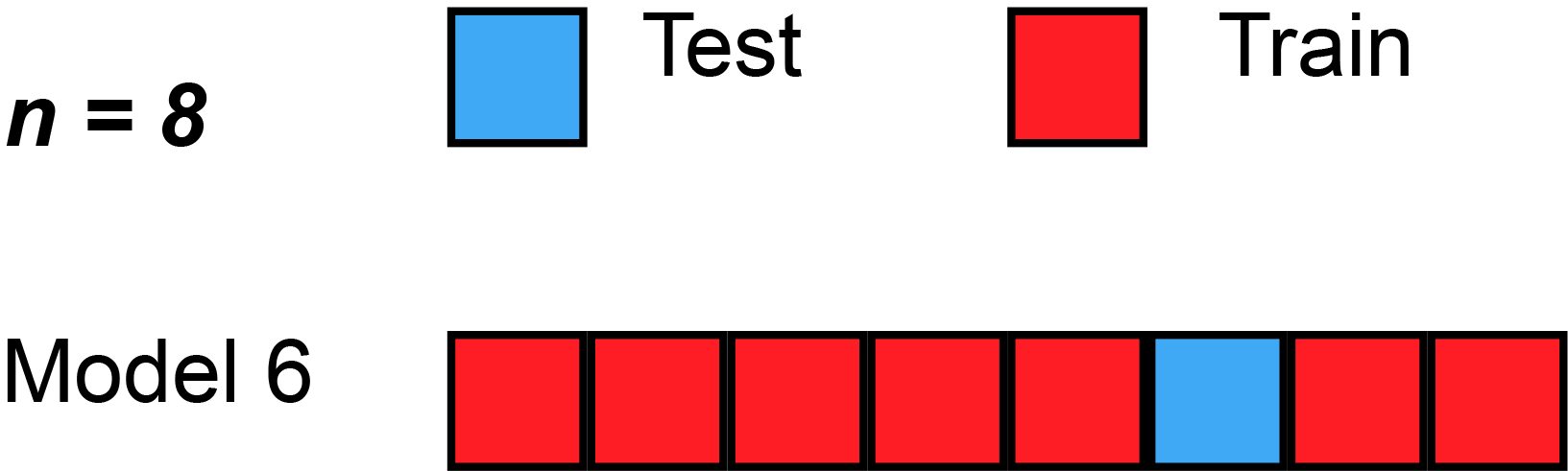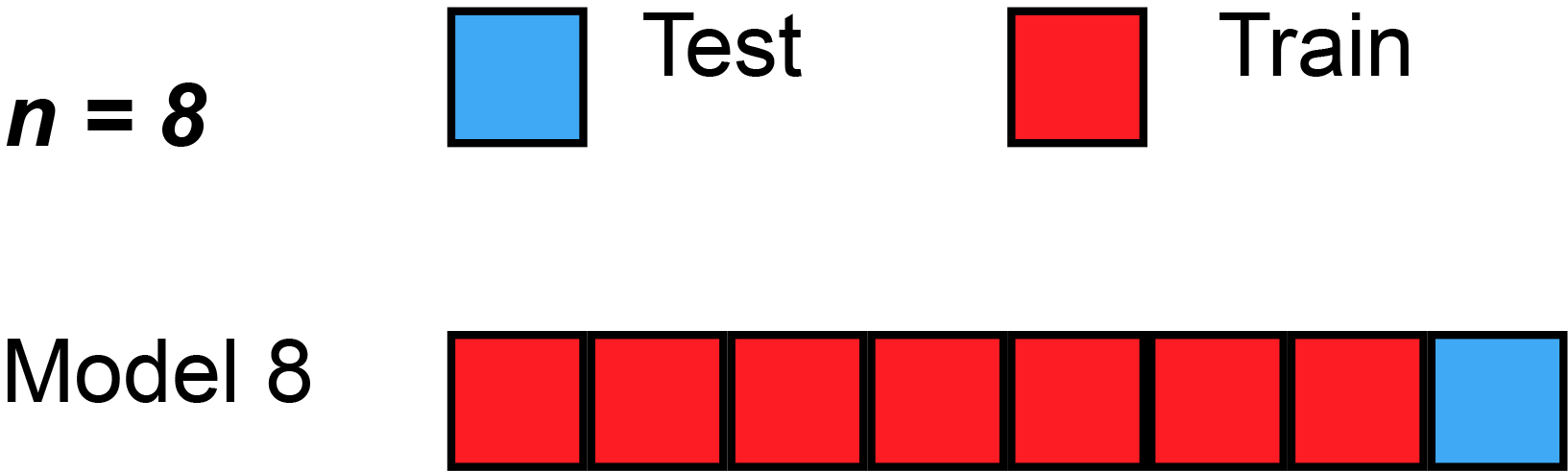
- Data si rozděluje na 3 množiny
- Trénovací
- Validační
- Testovací
- Musí se dát pozor na přeučení
- Možné použít cross-validaci
- Embedded method
- Like wrapper, the search is controlled by the algorithm constructing classifier
- Nejprve se naučí zvolený klasifikátor na všech příznacích, následně je vždy příznak odebrán a klasifikátor naučen na této podmnožině příznaků - Pokud se predikce zlepšila, tak jde dál, pokud se zhoršila, tak ten odebraný příznak zas vrátí
- záleží na pořadí odebírání příznaků
- Relativně robustní proti přeučení
Metriky, které se používají při porovnávání dat¶
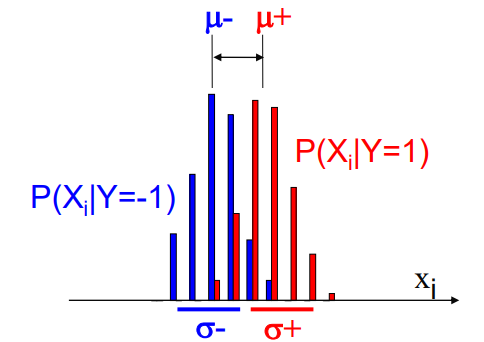
- T-test
- Slouží k zjištění, zda střední hodnota rozdělení Y=0 je stejná jako střední hodnota rozdělení pro Y=1
- Korelace
- Vzájemný lineární vztah mezi proměnnými
- Nejčastěji počítána pomoci Pearsonova korelačního koeficientu
-
\rho_X,Y = \dfrac{cov(X,Y)}{\sigma_X\sigma_Y} = \dfrac{E{(X-\mu_X)(Y-\mu_Y)}}{\sigma_X\sigma_Y}
-
- Entropie
- kvantifikuje očekávané množství informace, které příznak nese
- pokud příznak produkuje méně pravděpodobnou hodnotu Y, pak je nejspíše informace důležitější