Projekcni-metody #PCA #ICA #LDA #Sammon-mapping

Projekční metody

• snaha nalezení projekce dat z n dimenzionálního prostoru do k (k < n) dimenzionálního prostoru při zachování nějaké formy informací

• výhody

  • redundantní informace jsou často vyřazeny

• nevýhody

  • nová podoba dat je těžko interpretovatelná

• Je důležité zachovat korelaci mezi jednotlivými body i po projekci

  • Nejčastěji se používá Pearsonův korelační koeficient
  • $$\rho_X,Y = \dfrac{cov(X,Y)}{\sigma_X\sigma_Y} = \dfrac{E{(X-\mu_X)(Y-\mu_Y)}}{\sigma_X\sigma_Y}$$

Techniky

• Lineární techniky
  • Random mapping
  • PCA - Principal Component Analysis
  • ICA - Independent Component Analysis
  • LDA - Linear Discriminant Analysis
• Nelineární techniky
  • MDS
  • Sammon mapping

Random Mapping

• Používá random $k \times d$ matici $R$
  • $X_{k \times N}^{RP} = R_{k \times d}X_{d \times N}$
• Založena na Lindenstraussově lemmatu
  • Pokud je cílová dimenze vhodná, pak jsou vzdálenosti mezi projektovanými body cca zachovány
• Jde spíše o transformace než o projekci

PCA

• Cílem PCA je redukovat dimenzionalitu dat a zároveň zachovat co nejvíce variaci (odpovídá množství informace) přítomné v datasetu.
  • Aka snaha minimalizovat information loss
• Možným výpočtem je prolnutí přímky těžištěm, zkusit přímkou rotovat a tím zjistit nejlepší úhel.
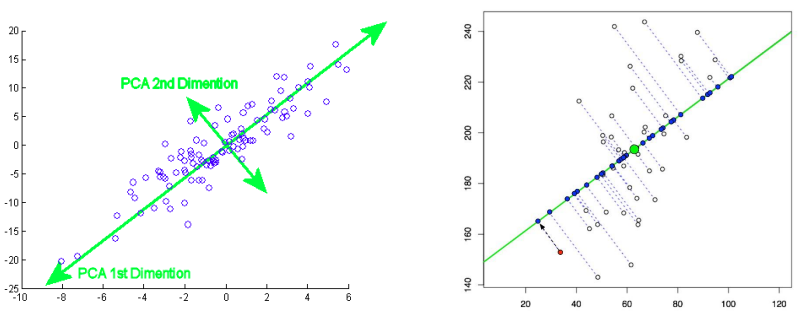
• Oproti LDA vrací prvky, které jsou více “výřečné” (more expressive features)
• Problémy
  • Nalezené hlavní komponenty nemusí najít správný pattern klasifikace
  • Viz obrázek PCA by vybralo komponentu s větším rozptylem
  • 

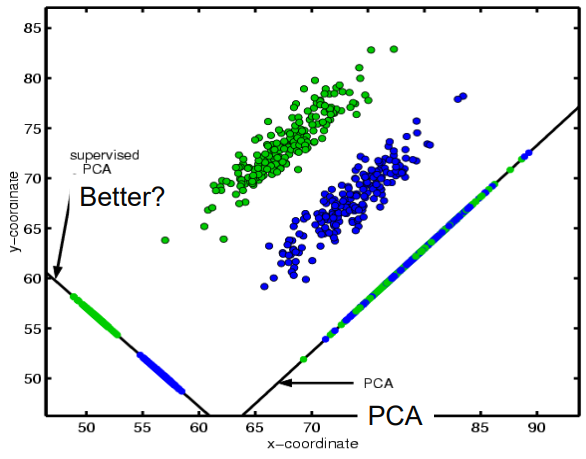
Information loss

• Redukce dimenze implikuje stratu informaci
• $min ||X - \hat{X}||$
• „Nejlepší“ podprostor je vycentrován na střední hodnotu vzorku a má směry určené „nejlepšími“ vlastními vektory kovariantní matice dat $X$.
  • Nejlepší vlastní vektor je takový který ma největší rozptyl

ICA

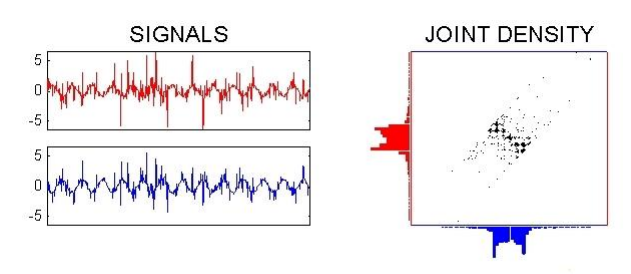
• Statistická technika, která se používá k oddělení multivarietního signálu na jeho nezávislé složky.
• Najde lineární kombinace původních signálů, které jsou navzájem statisticky nezávislé
• Spíše vhodné pro slepé rozdělení dat do tříd
• Problémy
  • Extrahovaný signál může být zrcadlen (otáčíme jim tak dlouho, až ho vezmeme i z druhé strany (+180°))
  • Nemá jasné pořadí komponent

LDA (Fisher projection)

• Projekce dat do nižší dimenze, kdy důraz je kladen na zachování diskriminačních informací (misclassification error)
• Maximální dimenze nového podprostoru je C-1 (C = počet uvažovaných tříd)
• Dobré pro klasifikaci tříd
• Snaha o maximalizaci vzdálenosti průměrů tříd a minimalizaci rozptylu uvnitř tříd
• 
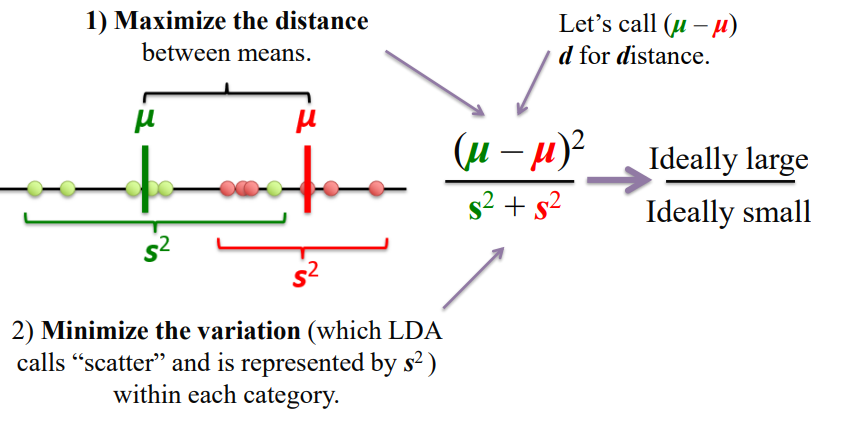
• Pokud není matice vnitřních rozptylů Sw singulární, může se použít nejdříve PCA na redukci dim a pak LDA k nalezení nejdiskriminativnějších směrů

PCA vs ICA vs LDA

• PCA
  • Lepší na malých datech
  • Získání nejexpresivnějších příznaků
  • Dobre na redukci dimenzi
• ICA
  • Nejlepší při slepém oddělování zdrojů, kdy nemáme k dispozici predikovanou třídu
• LDA
  • Na velkých a reprezentativních datech pro každou třídu, získání nejrozlišitelnějsích příznaků

Sammon mapping

• Metoda zobrazení vícerozměrných dat do nižšího rozměru, která se snaží zachovat relativní vzdálenosti mezi jednotlivými daty co nejlépe.
• Netransformuje souřadnice, místo toho reorganizuje pozice vzorů v novém prostoru.
• Cílí na minimalizaci tzv. Sammon’s stress error funkce
  • $$E = \dfrac{1}{\sum_{i<j}{d^*_{ij}}}\sum_{i<j}{\dfrac{(d^*_{ij}-d_{ij})^2}{d^*_{ij}}}$$
  • $d^*_{ij}:$ vzdalenost bodu $i,j$ v puvodni dimenzi
  • $d_{ij}:$ vzdálenost bodů $i,j$ v nové projekci
  • Minimalizace se může provádět Gradientním Sestupem