Time-series-filtering #Wedge #DTW #LCS #Landmarks #PAA #APCA¶

Předzpracovaní časových řad¶

U časových řad můžeme pozorovat
- podobnost na základě
  - tvaru
  - struktury celkové řady
- vzdálenost 2 časových řad

Příprava pro porovnávaní časových řad¶

Translace offsetu
- Nastavením offsetu “shodíme” časovou řadu k ose x
Normalizace
- Nastaveni stejné škály
  - Například od $< -1 ; 1 >$
Odebrání trendu
- Potřebuje znalost signálu
Odstranění šumu
- Smoothing

Euklidova vzdálenost¶

Jedna se o běžný způsob spočtení vzdálenosti dvou signálů
Rovnice
- Mějme dva signály $Q,C$
- $Q=q_1...q_n$
- $C=c_1...c_n$
- Chceme spočítat Euklidovu vzdálenost
  - $D(Q,C)= \sqrt{\sum_{i=1}^n(q_1-c_1)^2}$

Early abandon¶

Princip při kterém přestaneme porovnávat dva signály v případě ze se překročí nějaká stanovena chyba
Chyba se počítá jako kontinuální suma dvou signálů

Wedge¶

Mějme 2 časové řady. obsah mezi nimi nazýváme wedge, hranici bound
Na základě vzdáleností signálu od boundů se určuje, jestli kandidát patří do daného shluku
Použití
- Techniky shlukovaní
- Querying

DTW (Dynamic Time Warping)¶

Algoritmus pro měření podobnosti mezi dvěma časovými řadami, které se mohou odlišovat rychlostí a časem
Založeno na myšlence, že můžeme prodloužit každou sekvenci opakováním předchozích naměřených hodnot
Tvoří jakousi cestu mezi dvěma časovými řadami
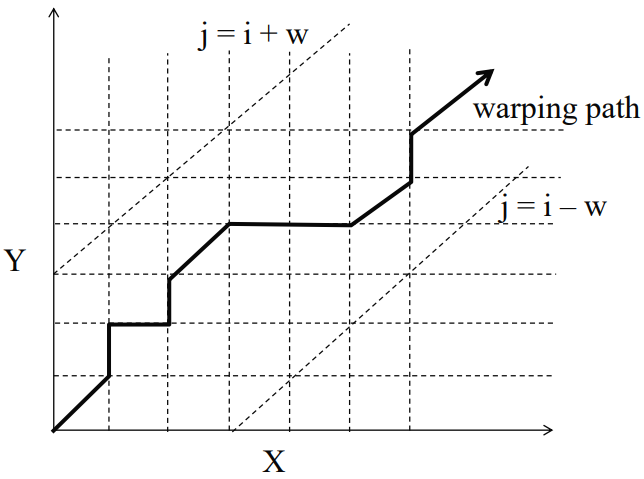
Omezeni
- Monotónnost - cesta maticí by neměla jít dolů nebo doleva (nemůžeme se vracet do minulosti)
- Žádný prvek by neměl být vynechán
- Warping window $= | i - j | \leq w$
Často se řeší pomocí dynamického programování

LCS (Longest Common Subsequence)¶

Jedna se o standartni LCS z BI-AAG - Mějme dva řetězce - $X=\{3,2,5,7,4,8,10,7\}$ - $Y=\{2,5,4,7,3,10,8,6\}$ - $LCS(X,Y)= \{2,5,7,10\} \lor \{2, 5, 4, 10\} \lor \{2, 5, 4, 8\} \lor \{2, 5, 7, 8\}$

Landmark¶

Reprezentuje časovou řadu body, kde se první derivace = 0 (resp. 2. derivace)

Aggregate approximation¶

Obecná myšlenka
- Časová řada je rozsekaná na části a ty se zprůměrují
Metody
- PAA
  - Rozdělení serie na stejne velke kusy
- APCA
  - Rozdělení serie na různě velké kusy
  - Snaží se udržet přesnost
- SAX
  - Rozdělení série na symboly a kódovaní série v symbolech