10. Paralelní Redukce & Prefix sum

Redukce

Definice

V paralelním zpracování dat je redukce klíčovým konceptem, který umožňuje kombinovat více datových prvků za použití určité binární operace (např. sčítání, násobení) a vypočítat tak jediný výsledný prvek.

Máme množinu s $n$ čísly, kterou potřebujeme sloučit do jedné hodnoty pomocí určité binární operace, například součtu.

Sekvenční složitost

• Lower bound: $SL(n) = \Omega(n)$, což značí, že se sekvenční složitost algoritmu pohybuje aspoň v řádu $n$.
• Upper bound: $SU(n) = O(n)$, což značí, že se sekvenční složitost algoritmu pohybuje nejvýše v řádu $n$.

PRAM implementace / Nepřímý strom

PRAM, Parallel Random-Access Machine, je teoretický model, který se používá pro analýzu paralelních algoritmů.

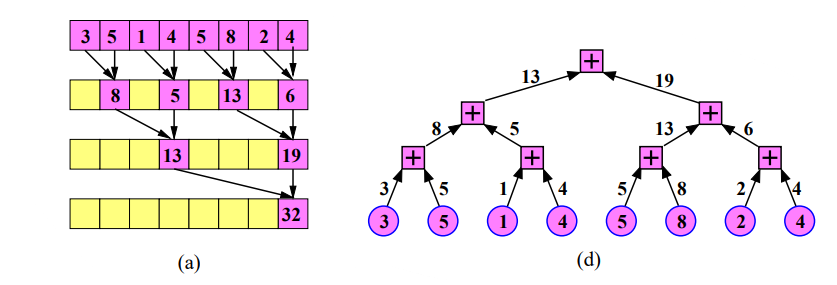
Algoritmus

1. Inicializace dat: Na počátku algoritmu se vstupní data rozdělí mezi dostupné procesory.

2. Lokální redukce: Každý procesor provede lokální redukci na své podmnožině dat. Lokální redukce znamená aplikaci požadované operace (např. součet) na svých datech.

3. Globální redukce (Nepřímý stromový algoritmus)

   1. Máme $p$ procesorů, které potřebují provést redukci.
   2. Provedeme $\log(p)$ kroků.
   3. V každém kroku se provede požadovaná operace na prvcích, které jsou $2^k$ daleko od sebe, kde $k$ je počet aktuálního kroku.
   4. Procesor s nižším ID se deaktivuje a nebude se dále podílet na výpočtu.
   5. Výsledky jsou ukládány do původního pole.

Hyperkrychle / 1-D WH mřížka / Přímý strom

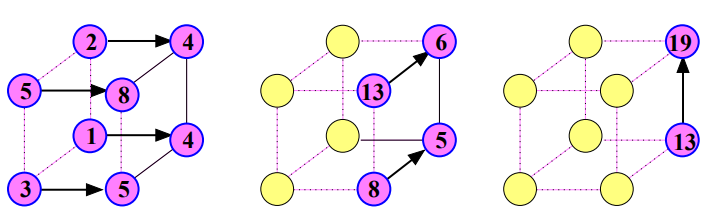
Algoritmus

1. Inicializace dat: Na začátku algoritmu se vstupní data (prvky) rozdělí mezi dostupné procesory.

2. Lokální redukce: Každý procesor vykoná lokální redukci na své podmnožině dat. To znamená, že procesor provede požadovanou operaci (např. součet) na svých datech a uloží výsledek.

3. Globální redukce:

   1. Iterativní propojení vrcholů: Pro každou dimenzi hyperkrychle od $i = 0$ po $d-1$, každý procesor vypočítá svého partnera v dimenzi $i$ a provede následující kroky:
      • Komunikace: Procesor $j$ pošle svou hodnotu svému partnerovi v dimenzi $i$.
      • Redukce: Pokud procesor $j$ má nižší index než jeho partner, provede operaci redukce s hodnotou, kterou obdržel od partnera, a uloží výsledek.
      • Aktualizace stavu: Procesory s vyšším indexem v dimenzi $i$ přestávají být součástí výpočtu.

4. Uložení a sdílení výsledku: Po dokončení iterací je výsledek globální redukce uložen v procesoru s indexem 0. Pokud je třeba, procesor 0 může následně rozeslat výsledek redukce ostatním procesorům.

Slozitost paralelnich algoritmu

Měření výkonnosti paralelních algoritmů je zásadní pro určení jejich efektivity a škálovatelnosti. Následující tabulka shrnuje klíčové metriky:

Paralelni cas	Cena behu	Efektivnost
$T(n, p) = O\left(\frac{n}{p} + \log p\right)$	$C(n, p) = O(n + p \log p)$	$E(n, p) = \Theta\left(\frac{n}{n + p \log p}\right)$
$\psi_1(p) = p \log p$	$\psi_2(n) = \frac{n}{\log n}$	$\psi_3(n) = \frac{n}{\log n}$

MPI funkce

MPI (Message Passing Interface) je standard pro komunikaci mezi procesory, který se hojně používá v paralelním programování. Následující funkce jsou určené pro práci s redukcí:

• MPI_Reduce: Sjednocuje data z více procesů do jednoho pomocí zvolené operace (např. součet) a ukládá výsledek na určený root procesor.

• MPI_AllReduce: Funguje podobně jako MPI_Reduce, ale rozesílá výsledek redukce všem procesorům, což umožňuje synchronizaci stavu mezi nimi.

• MPI_Reduce_scatter_block: Kombinuje chování MPI_Reduce s následným rozdělením výsledku mezi všechny procesory v rovnoměrných blocích.

Dodatečné Poznámky

Při vývoji paralelních algoritmů pro redukci je důležité pečlivě zvolit vhodnou topologii komunikační sítě (jako hyperkrychle) a algoritmů (přímý nebo nepřímý strom). Výběr vhodné topologie a algoritmu může mít významný vliv na výkon, škálovatelnost a efektivnost algoritmu. Kromě toho je třeba brát v úvahu reálné omezení hardware a komunikace při implementaci těchto algoritmů v praktických aplikacích.

Prefix sum

Definice

Máme pole seřazených $n$ čísel, a ke každému číslu v poli přičteme součet čísel, která jsou před ním v poli.

Sekvenční složitost

• Dolní mez: $SL(n)=\Omega(n)$
• Horní mez: $SU(n)=O(n)$

PRAM implementace

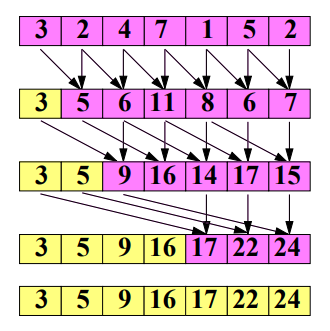
Algoritmus

1. Inicializace dat: Na začátku algoritmu jsou vstupní data (prvky) rozdělena mezi dostupné procesory.

2. Lokální prefixový součet: Každý procesor vypočítá lokální prefixový součet na své části dat.

3. Globální prefixový součet:

   1. Máme $p$ procesů, které potřebují vypočítat prefixový součet.
   2. Provedeme $\log(p)$ kroků.
   3. V každém kroku se provede součet prvků, které jsou $2^k$ vzdáleny od sebe.
   4. Tyto hodnoty se uloží do původního pole.

Hyperkrychle

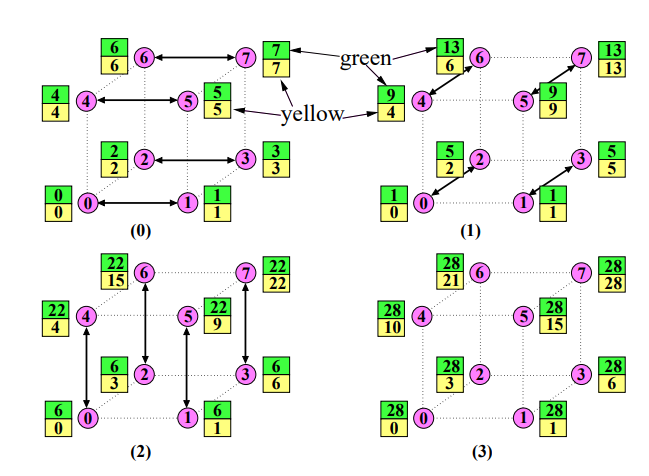
Algoritmus

1. Inicializace dat: Na začátku algoritmu jsou vstupní data (prvky) rozdělena mezi dostupné procesory.

2. Lokální prefixový součet: Každý procesor vypočítá lokální prefixový součet na své části dat. Do "žluté" a "zelené" proměnné uloží poslední číslo (číslo s nejvyšším indexem).

3. Globální prefixový součet:

   1. Linearizace: Všechny uzly v síti se indexují tak, aby bylo možné mluvit o jejich pořadí. V hyperkrychlích použijeme lexikografické indexování.
   2. Iterativní propojení uzlů: Pro každou dimenzi hyperkrychle od $i = 0$ do $d-1$, každý procesor vypočítá svého partnera v dimenzi $i$ a provede následující kroky:
      • Komunikace: Procesor $j$ pošle svou "zelenou" proměnnou partnerovi v dimenzi $i$.
      • Přičtení: Hodnotu od souseda přičte k "zelené" proměnné. Pokud má soused nižší index, tak přičte hodnotu i k "žluté" proměnné.

4. Lokální dopočítání prefixového součtu: Po dokončení iterací je výsledek globálního prefixového součtu uložen v "žlutých" proměnných jednotlivých procesorů. Tyto "žluté" proměnné se poté pošlou sousedovi s o 1 vyšším indexem a přičtou se k lokálním proměnným tohoto souseda.

Prime/neprime stromy, WH Site

Algoritmus

1. Inicializace dat: Na začátku algoritmu jsou vstupní data (prvky) rozdělena mezi dostupné procesory.

2. Lokální redukce: Každý procesor vypočítá lokální prefixový součet na své části dat.

3. Globální redukce:

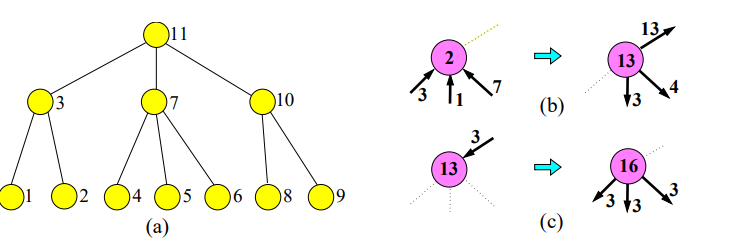
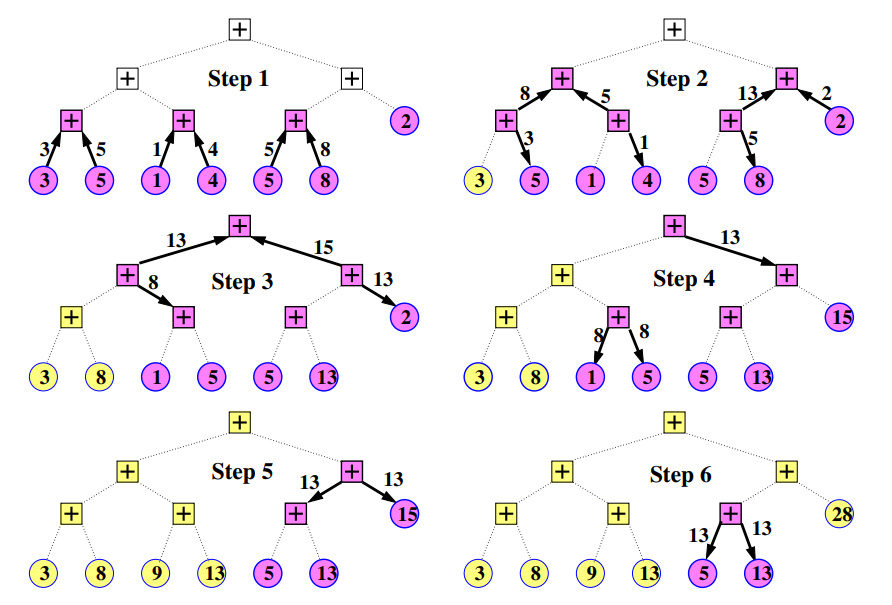
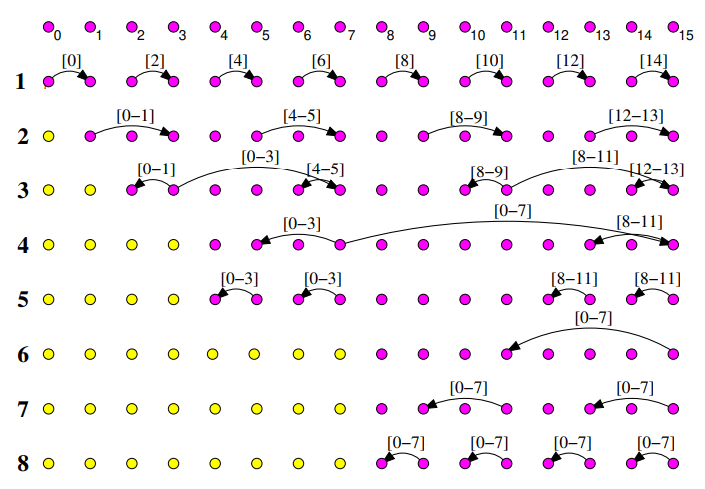
   1. Linearizace: Pokud je to potřeba, provede se indexace uzlů, aby bylo možné mluvit o jejich pořadí. V případě stromů se použije postorder indexace. WH uzly se budou chovat jako simulovaný nepřímý strom.
   2. Iterativní propojení uzlů: Začínáme u listů a postupně jdeme až ke kořenu. V každém kroku se stane jedna z možností:
      1. Výsledek jde od potomků. Tyto hodnoty se postupně sečtou a odesílají se postupně více pravým potomkům (v případě přímého stromu se přičte i hodnota uzlu) a nakonec se odesílají i rodiči.
      2. Přijde výsledek od rodiče, pak se stejný výsledek pošle potomkům (pokud je to přímý strom, přičte se i hodnota uzlu).

4. Lokální dopočítání prefixového součtu: Po dokončení iterací je výsledek globálního prefixového součtu uložen v jednotlivých procesorech. Tyto hodnoty se poté pošlou sousedovi s o 1 vyšším indexem a přičtou se k lokálním hodnotám tohoto souseda.

SF site

Algoritmus

1. Inicializace dat: Na začátku algoritmu jsou vstupní data (prvky) rozdělena mezi dostupné procesory.

2. Lokální redukce: Každý procesor vypočítá lokální prefixový součet na své části dat.

3. Globální redukce:

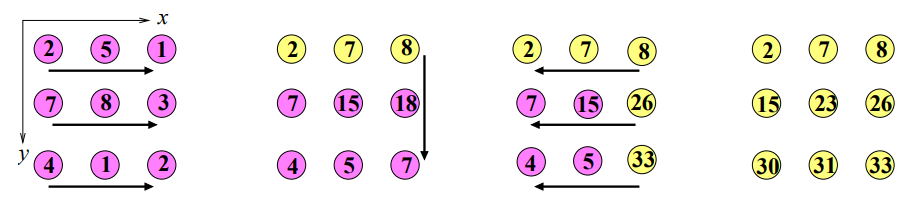
   1. Linearizace: V případě 2D SF sítě se použije linearizace po řádcích (row-wise).
   2. Horizontální prefixové součty: Všechny uzly postupně vypočítají prefixový součet až do konce řádku.
   3. Vertikální prefixové součty: Konce řádků vertikálně vypočítají prefixový součet.
   4. Horizontální zpětný průchod: Z konce řádku se zpětně pošle prefixový součet, aby byly aktualizovány i hodnoty v horizontálních řádcích.

4. Lokální dopočítání prefixového součtu: Po dokončení iterací je výsledek globálního prefixového součtu uložen v jednotlivých procesorech. Tyto hodnoty se poté pošlou sousedovi s o 1 vyšším indexem a přičtou se k lokálním hodnotám tohoto souseda.

Složitost paralelních algoritmů

Paralelni cas	Cena behu	Efektivnost
$T(n, p) = O\left(\frac{n}{p} + \log p\right)$	$C(n, p) = O(n + p \log p)$	$E(n, p) = \Theta\left(\frac{n}{n + p \log p}\right)$
$\psi_1(p) = p \log p$	$\psi_2(n) = \frac{n}{\log n}$	$\psi_3(n) = \frac{n}{\log n}$

MPI funkce

• MPI_Scan: Pro každý proces vrátí prefixový součet dat až po daný proces včetně jeho vlastních dat.

• MPI_Exscan: Podobné jako MPI_Scan, ale vrátí prefixový součet dat až po proces předchozí, tedy nezahrnuje data vlastního procesu.

Řešení Zhušťovacího Problému

Úvod

Zhušťovací problém, známý také jako Stream Compaction, se vztahuje na efektivní rozdělení prvků pole do dvou skupin pomocí paralelního zpracování. Tento problém je zásadní v oblasti paralelního programování, kde se snažíme maximalizovat využití výpočetních zdrojů, minimalizovat latenci a zvýšit propustnost.

Kroky Řešení

1. Prefixový Součet (Prefix Sum): Aplikujeme operaci prefixového součtu na pole na základě flagů prvků. Získáme nové pole, kde každý prvek označuje počet prvků s určitým flagem, které předcházejí danému indexu.

2. Rozdělení Prvků: Vytvoříme dvě výstupní pole pro prvky s flagem 0 a 1. Umístíme prvky na odpovídající indexy v těchto polích podle výsledků prefixového součtu. Konkrétně, pokud $A[i]$ má flag 1, umístíme prvek na index $P[i]-1$ v poli s flagem 1, a obdobně pro flag 0.

Paralelní RadixSort

Úvod

Radix Sort je klasický řadící algoritmus, který seřazuje čísla na základě jednotlivých číslic. Paralelní Radix Sort je varianta tohoto algoritmu optimalizovaná pro paralelní zpracování, což vede k významným zrychlením, zejména pro velká data.

Kroky Řešení

1. Binární Převod: Čísla v poli převedeme na binární formát. Tento krok umožňuje manipulaci s jednotlivými bity, což je klíčové pro Radix Sort.

2. Zhušťování a Řazení: Pro každý bit od nejméně významného po nejvýznamnější aplikujeme zhušťovací algoritmus, který rozdělí čísla na základě hodnoty bitu do dvou skupin. Toto rozdělení nám umožní izolovat vliv jednotlivých bitů na konečné seřazení.

3. Sloučení Výsledků: Po aplikaci zhušťovacího algoritmu na každý bit, musíme výsledky sloučit tak, aby byla vytvořena finální seřazená posloupnost. Toho lze docílit sledováním pozice každého prvku během procesu a sloučením výsledků v souladu s těmito pozicemi.

Sčítačka s predikcí přenosu

Úvod

Sčítačka s predikcí přenosu (Carry-Lookahead Adder) je pokročilá forma paralelní sčítačky, která usiluje o minimalizaci časových prodlev spojených s přenosem carry bitů. Cílem je sečíst dvě čísla paralelně s časovou složitostí $\mathcal{O}(\log(n))$, což nám umožňuje překonat omezení spojená se sériovým přenosem carry bitu.

Kroky Řešení

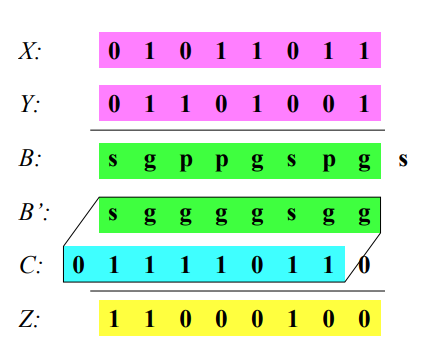
1. Inicializace Pole B: Vytvoříme pole $B$, které bude obsahovat tři možnosti: $P$ (propagate), $G$ (generate) a $S$ (stop). Rozhodujeme se podle následující tabulky:

x/y	0	1
0	S	P
1	P	G

1. Modifikace Pole B: Použijeme prefixový součet k modifikaci pole B tak, že bude obsahovat pouze $G$ (generate) a $S$ (stop). Výběr se provádí podle tabulky:

$X*Y$	S	P	G
S	S	S	S
P	S	P	G
G	G	G	G

1. Vytvoření Carry Pole: Na základě modifikovaného pole $B$ vytvoříme pole carry bitů paralelně. Pokud je $B_{i-1} = G$, potom $C_i = 1$.

2. Výpočet Součtu: Nakonec vypočítáme součet paralelně s použitím pole carry bitů. Výsledný součet $S$ bitu $i$ je dán jako $S_i = A_i \oplus B_i \oplus C_{i-1}$.

Segmentový paralelní prefixový součet

Definice

Segmentový paralelní prefixový součet je specifická varianta algoritmu prefixového součtu, která umožňuje provádět výpočet v rámci diskrétních segmentů vstupního pole. Každý segment je definován jako souvislá podmnožina prvků pole, uvnitř které je prefixový součet vypočítán izolovaně. Tento algoritmus je obzvláště užitečný v paralelním zpracování, kde umožňuje efektivní výpočet prefixových součtů v rámci různých částí dat simultánně.

roky Řešení

• Krok 1: Definice Operátoru
  • Definujeme speciální binární operátor, označujme jej $\odot$, který nám umožní rozlišit, zda jsme na levé hranici segmentu. Operátor je definován následující tabulkou, kde $x$ a $y$ jsou prvky vstupního pole, a $x \odot y$ je výsledek operace:

$x\odot y$	$y$	$\lvert y$
$x$	$x\odot y$	$\lvert y$
$\lvert x$	$\lvert (x\odot y)$	$\lvert y$

Zde $|x$ a $|y$ představují hodnoty prvků ležící na levé hranici segmentu.

• Krok 2: Použití Operátoru pro Prefixový Součet
  • Aplikujeme standardní algoritmus prefixového součtu na vstupní pole, ale s použitím nově definovaného operátoru $\odot$. Tímto způsobem je vypočítán prefixový součet izolovaně v rámci každého segmentu, protože operátor bere v úvahu, zda je aktuální prvek na levé hranici segmentu.

Segmentovy paralelni quicksort

Úvod

Segmentový paralelní Quicksort je adaptace klasického Quicksort algoritmu, který je optimalizován pro paralelní zpracování dat rozdělených do segmentů. Algoritmus umožňuje více vláknům pracovat na různých částech dat souběžně, což může výrazně zvýšit rychlost řazení, zejména pro velká data.

Kroky Řešení

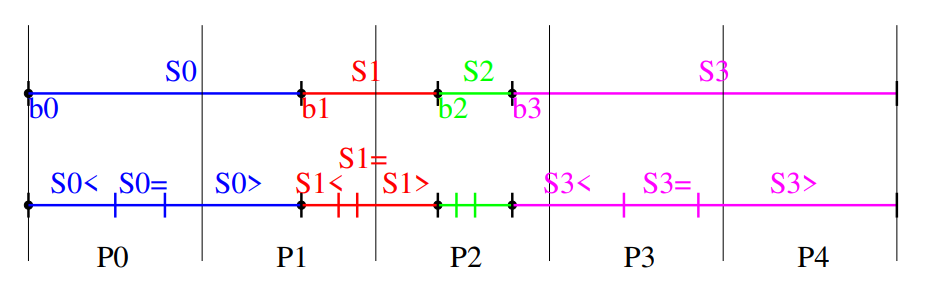
• Krok 1: Výběr a Distribuce Pivotu

  • Vybereme první prvek v každém segmentu jako pivot a distribuujeme ho mezi vlákna, která zpracovávají daný segment. Toto je provedeno s použitím operace prefixového součtu s identitní operací $a*b=a$.

• Krok 2: Segmentový Prefixový Součet pro Menší Prvky

  • Pro prvky, které jsou menší než pivot, aplikujeme segmentový paralelní prefixový součet. Následně broadcastujeme index, kde končí prvky menší než pivot, mezi vlákna zpracovávající tento segment.

• Krok 3: Segmentový Prefixový Součet pro Rovné Prvky

  • Pro prvky rovné pivotu, opět aplikujeme segmentový paralelní prefixový součet. Broadcastujeme maximální index těchto prvků mezi vlákna.

• Krok 4: Segmentový Prefixový Součet pro Větší Prvky

  • Pro prvky, které jsou větší než pivot, aplikujeme segmentový paralelní prefixový součet. Broadcastujeme index prvního prvku, který je větší než pivot, mezi vlákna.

• Krok 5: Rekurze s Novými Segmenty

  • Následně prohodíme tři segmenty (menší, rovné a větší než pivot) tak, aby byly uspořádány v tomto pořadí. Vytvoříme tři nové podsegmenty a rekurzivně opakujeme postup od kroku 1 pro každý podsegment.

• Krok 6: Kontrola Konce

  • Abychom zjistili, zda můžeme ukončit rekurzi, provedeme redukci s operací $x < y$ napříč segmenty. Pokud je splněna podmínka ukončení (typicky když je velikost segmentu rovna 1), rekurze končí.