12. Násobení matic

Násobení husté matice vektorem

Při násobení husté matice vektorem, máme matici $A$ patřící do množiny $R^{n,n}$ a vektor $v$ patřící do množiny $R^n$. Úkolem je vypočítat násobení vektoru maticí, $y=Ax$. Tento proces můžeme zobrazit pomocí několika mapovacích algoritmů: řádkové mapování, sloupcové mapování a šachovnicové mapování. Každý z těchto algoritmů má své vlastní definice, algoritmy a složitost, které jsou níže podrobně popsány.

Řádkové mapování

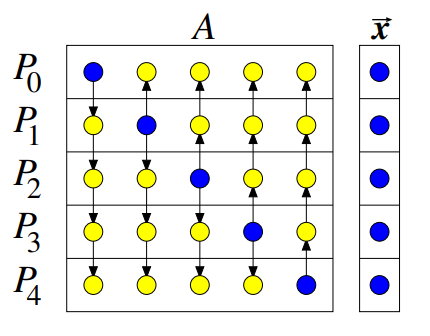
Definice

Matice je rozdělena do $p$ vláken, přičemž každé vlákno zpracovává $n/p$ řádků matice. Dále každé vlákno dostane odpovídající $n/p$ část vektoru $x$.

Algoritmus

1. Distribuce dat: V prvním kroku procesy rozešlou svou část vektoru všem ostatním procesům. Toto je realizováno pomocí funkce MPI_AllToAll.
2. Paralelní výpočet: V druhém kroku procesy paralelně vypočítají své části vektoru.
3. Shromažďování výsledků: Výsledek se nachází po řádcích v jednotlivých procesech.

Složitost

• Paměťová složitost: Každý procesor musí udržet celou řádku a celý vektor $x$, takže paměťová složitost je $O(2n)$.
• Časová složitost: Každý procesor musí nejprve komunikovat se všemi ostatními procesory. Počet těchto komunikací závisí na architektuře propojovací sítě, obecně to může být $n$. Dále se musí provést lokální násobení, což bude $n/p$. Tedy časová složitost tohoto algoritmu je $O(n+n/p)$.
• Škálovatelnost: Tento algoritmus má velmi dobrou škálovatelnost, protože konstantní efektivnost lze dosáhnout i pro konstantní počet řádků.

Sloupcové mapování

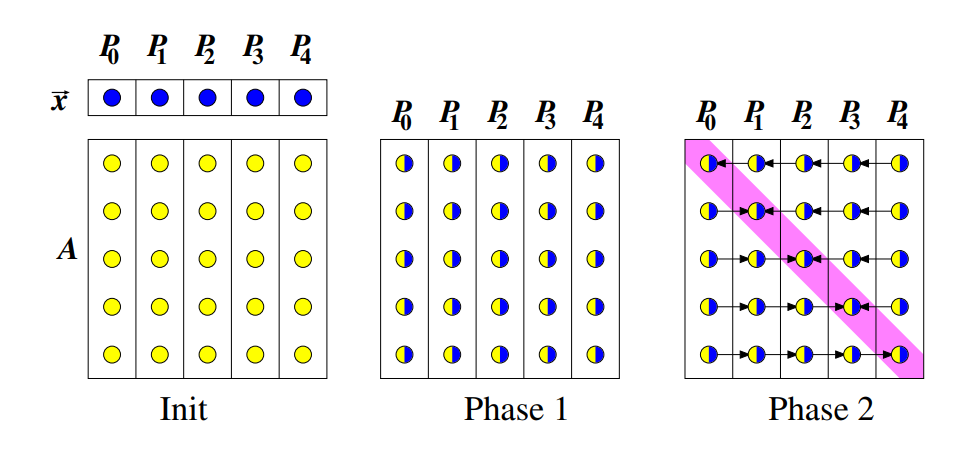
Definice

Podobně jako u řádkového mapování, matice je rozdělena do $p$ vláken, avšak nyní každé vlákno zpracovává $n/p$ sloupců matice. Každé vlákno rovněž dostane odpovídající $n/p$ část vektoru $x$.

Algoritmus

1. Paralelní výpočet: V prvním kroku procesy paralelně vypočítají své části vektoru a každý procesor tedy zná svůj příspěvek k výsledku.
2. Redukce na hlavní diagonálu: V druhém kroku je provedena redukce na hlavní diagonálu.
3. Shromažďování výsledků: Výsledek se nachází na diagonále v příslušných procesech.

Složitost

• Paměťová složitost: Každý procesor musí udržet část sloupců a celý vektor $v$, takže paměťová složitost je $O(2n)$.
• Časová složitost: Stejně jako u řádkového mapování je časová složitost $O(n+n/p)$.
• Škálovatelnost: Sloupcové mapování také vykazuje vysokou míru škálovatelnost.

Šachovnicové mapování

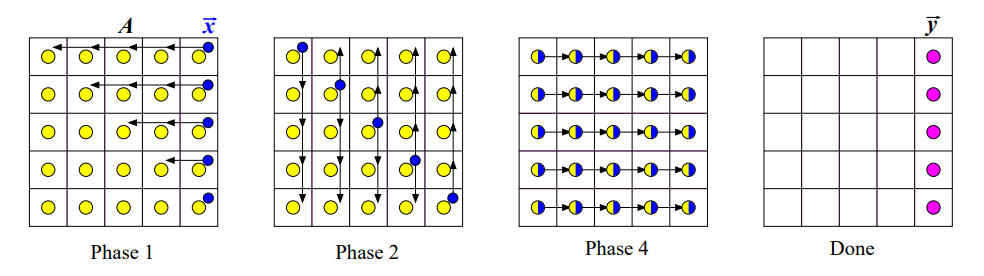
Definice

V této metodě se matice $A$ považuje za 2D mřížku a vektor $v$ se mapuje libovolně na poslední sloupec nebo hlavní diagonálu.

Algoritmus

1. Distribuce subvektorů: V prvním kroku se pošlou dílčí vektory na hlavní diagonálu pomocí point-to-point komunikace.
2. Sloupcový broadcast: V druhém kroku se pošlou hodnoty dílčího vektoru z diagonály po sloupcích.
3. Lokální výpočty: V třetím kroku procesory paralelně spočítají svou část submatice.
4. Řádková redukce: V čtvrtém kroku se provede redukce zpět na poslední sloupec.

Složitost

• Paměťová složitost: Každý procesor musí udržet část mřížky a část vektoru $v$, což dává paměťovou složitost $O(\frac{n^2}{p}+\frac{n}{p})$.
• Časová složitost: Komunikace point-to-point závisí na architektuře komunikační sítě, což může být například na 2D store and forward mřížka stejné jako pro broadcast a redukci, tedy $O(n)$. Časová složitost lokálního výpočtu bude $O(\frac{n}{\sqrt{p}}\sqrt{p})=O(n)$. Celková časová složitost je tedy $O(4n)$.
• Škálovatelnost: Šachovnicové mapování má také vysokou míru škálovatelnost.

Násobení hustých matic

Výpočetní algoritmy pro násobení matic jsou klíčovou součástí numerické lineární algebry. Zde se zaměříme na efektivní násobení dvou hustých čtvercových matic $A$ a $B$ o rozměrech $n \times n$, a budeme chtít získat matici $C$ takovou, že $C = AB$. Označme tedy matice jako $A \in \mathbb{R}^{n \times n}$, $B \in \mathbb{R}^{n \times n}$ a $C \in \mathbb{R}^{n \times n}$.

Cannonův algoritmus

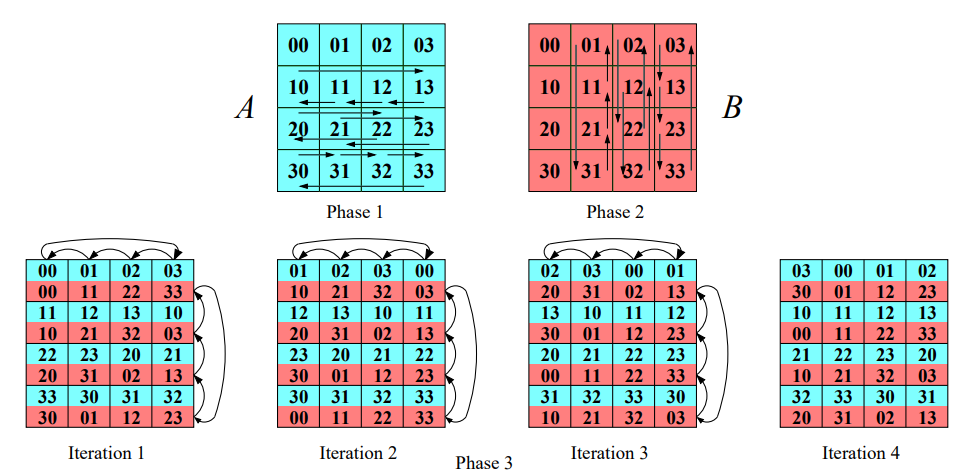
Cannonův algoritmus je založen na dělení matic na menší podmatice a provádění operací na těchto podmaticích paralelně. V tomto algoritmu je důležitá struktura komunikační sítě, kterou představuje 2D torus.

Předpokládejme, že máme $p$ vláken a každé vlákno pracuje s maticí o rozměru $\sqrt{p} \times \sqrt{p}$.

Kroky algoritmu

1. Inicializace: V první fázi posuneme řádky matice $A$ o $i$ pozic doleva a sloupce matice $B$ o $i$ pozic nahoru, kde $i$ je index řádku resp. sloupce a $i \in {0, \dots, p-1}$.

2. Násobení a rotace podmatic: Nyní provedeme násobení jednotlivých podmatic lokálně. Po provedení násobení rotujeme každý řádek matice $A$ o jednu pozici doleva a každý sloupec matice $B$ o jednu pozici nahoru. Tyto kroky se opakují $p$-krát.

3. Sčítání výsledků: Každé vlákno sečte své výsledky do výsledné matice $C$.

Foxuv algoritmus

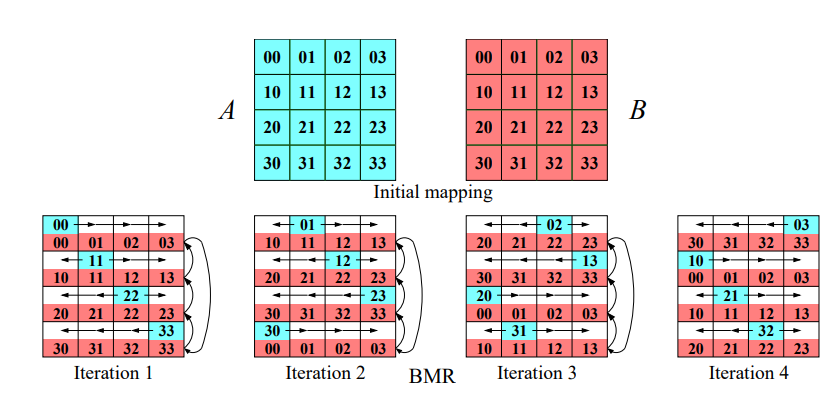
Foxův algoritmus je alternativní metodou k Cannonovu algoritmu, avšak s jiným způsobem komunikace mezi procesory. Opět využívá strukturu komunikační sítě 2D torus a pracuje s $p$ vlákny, kde každé vlákno pracuje s maticí o rozměru $\sqrt{p} \times \sqrt{p}$.

Kroky algoritmu

1. Broadcast matice $A$: V prvním kroku algoritmus provádí broadcast řádků matice $A$, začínajíc u hlavní diagonály.

2. Násobení a rotace podmatic: Vlákna následně vynásobí podmatice lokálně a rotují každý sloupec matice $B$ o jednu pozici nahoru. Tyto kroky se opakují $p$-krát.

3. Sčítání výsledků: Každé vlákno sečte své výsledky do výsledné matice $C$.

Implementace v MPI

MPI (Message Passing Interface) je standardní rozhraní pro programování paralelních počítačů. Níže jsou uvedeny kroky pro implementaci Cannonova nebo Foxova algoritmu pomocí MPI.

1. Vytvoření virtuální topologie: V MPI vytvoříme kartézskou topologii, která umožňuje procesorům komunikovat v mřížce.

2. Zjištění souřadnic procesoru: Každý procesor zjistí své souřadnice v kartézské síti.

3. Nastavení kartézského posunu: Pro rotaci matice nastavíme posun (shift) v kartézské topologii.

4. Rotace a komunikace: Provedeme rotaci podmatic pomocí funkce MPI_Cart_shift a vyměníme data mezi procesory pomocí funkce MPI_SendRecv_replace.

5. Lokální násobení a sčítání: Každý procesor vynásobí své podmatice a přičte je do své části výsledné matice.

Mocninná metoda

Mocninná metoda je iterativní algoritmus, jehož účelem je aproximace dominantního vlastního čísla matice. Má za cíl nalezení největšího vlastního čísla matice $A$ opakovaným násobením matice vektorem $\vec{x}$, tedy $y = A\vec{x}$.

Algoritmus

1. Inicializace: Vyberte libovolný nenulový počáteční vektor $\vec{x}$.

2. Matice-Vektor Násobení (MVM): Vypočítejte $\vec{y} = A\vec{x}$.

3. Normalizace: Spočítejte normu $\alpha$ vektoru $\vec{y}$: $$\alpha \leftarrow \|\vec{y}\|_2 = \sqrt{y_1^2 + y_2^2 + \ldots + y_n^2}$$

4. Aktualizace vektoru: Nahraďte vektor $\vec{x}$ normalizovaným vektorem $\vec{y}$: $\vec{x} = \frac{\vec{y}}{\alpha}$.

5. Konvergenční kritérium: Ověřte, zda je splněno konvergenční kritérium.

6. Opakování: Pokud není konvergenční kritérium splněno, vraťte se k kroku 2. V opačném případě algoritmus končí s $\alpha$ jako aproximací dominantního vlastního čísla.

Paralelní implementace

Existují různé způsoby, jak paralelizovat mocninnou metodu. Níže jsou uvedeny tři základní strategie: Náhodné mapování, Řádkové mapování a Šachovnicové mapování.

Náhodné mapování

Každý proces potřebuje celý vektor $\vec{x}$ a $\vec{y}$ pro výpočet své části $\vec{y}$. Na konci každé iterace je použita funkce MPI_Allreduce pro synchronizaci vektoru $\vec{x}$ a $\vec{y}$ mezi procesy.

Řádkové mapování

Každý proces potřebuje celý vektor $\vec{x}$ pro výpočet své části $\vec{y}$. Postupujeme následovně:

1. Provede se MPI_Allgather pro shromáždění celého vektoru $\vec{x}$.

2. Každý proces provede lokální výpočet své části $\vec{y}$.

3. Provede se lokální výpočet normalizace.

4. Vektor $\vec{y}$ se vyřeší normalizovaným výsledkem.

5. Ověří se konvergenční podmínka.

6. Pokud není splněna, vrátíme se k bodu 1.

Šachovnicové mapování

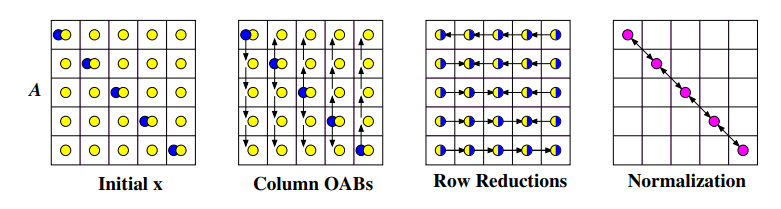
V této strategii každý proces potřebuje pouze svou část vektoru $\vec{x}$. Kroků je více:

1. Vektor $\vec{x}$ je namapován na hlavní diagonálu.

2. Procesy na diagonále posílají hodnoty vektoru po sloupcích (sloupcový broadcast).

3. Paralelně všechny procesory spočítají svou část submatice (lokální výpočty).

4. Provede se redukce zpět na diagonálu.

5. Provede se redukce diagonály.

6. Ověří se konvergenční podmínka.

7. Pokud není splněna, vrátíme se k bodu 2.

Implementace v MPI

• Vytvoříme nové komunikační skupiny pro řádky, sloupce a diagonálu.
• Pomocí MPI_Bcast provedeme sloupcový broadcast.
• Pomocí MPI_Reduce zpětně namapujeme hodnoty $\vec{x}$ na diagonálu.
• Pomocí MPI_AllReduce zjistíme normalizaci přes diagonálu.

Paměťová komplexita

Paměťová složitost na proces	Pole x	Pole y
Libovolné	$n$	$n$
Po řádcích	$n$	$\frac{n}{p}$
Šachovnicové	$\frac{n}{\sqrt{p}}$	$\frac{n}{\sqrt{p}}$

Paralelní generování náhodných permutací

Cílem je vygenerovat permutaci pole čísel paralelně pomocí více procesorů.

Algoritmus

1. Inicializace: Každý procesor $p_i$ si náhodně připraví destinace pro svoji část $\frac{n}{p}$ čísel.

2. Histogram: Každý procesor si lokálně spočítá histogram pro počet zpráv, které bude posílat jednotlivým procesorům.

3. Komunikace: Každý procesor pošle ostatním procesorům počet zpráv, které jim pošle.

4. Příjem dat: Každý procesor si připraví pole pro příjem dat.

5. Výměna dat: Každý procesor pošle ostatním procesorům svou permutaci čísel.

6. Vyvážení dat: Všechna data se vyváží pomocí prefixového součtu.

Implementace v MPI

1. Pro zjištění kolik dat každý procesor přijme bude sloužit MPI_AllToAll
2. Pro poslání variabilních dat pro všechny procesy se použije funkce MPI_AllToAllV