4. Základní paralelní algoritmy

11. Paralelizace výpočtu histogramu pomocí OpenMP¶

Histogram je grafické znázornění, které ukazuje frekvenci hodnot vstupního pole o velikosti $n$ , s určitým rozsahem hodnot označovaným jako range.

Standardní algoritmus – Časová složitost: $O(n) + O(range)$ ¶

Během inicializace nastavte všechny prvky výsledného pole na $0$ :

for (int i = 0; i < range; i++) {
    result[i] = 0;
}

Pro každý prvek vstupního datového pole inkrementujte odpovídající index ve výsledném poli:
```
for (int i = 0; i < n; i++) {
    result[data[i]] += 1;
}
```
Tato metoda načte každou hodnotu jednou a zahodí ji. Tento přístup je nevhodný pro paralelizaci kvůli nepřímé indexaci.

Paralelní řešení (Naivní přístup)¶

K paralelizaci smyčky využijte OpenMP #pragma omp parallel for společně s #pragma omp atomic update.

#pragma omp parallel for
for (int i = 0; i < n; i++) {
    #pragma omp atomic
    result[data[i]] += 1;
}

Tento přístup bude velmi neefektivní kvůli výpadkům cache (způsobeným nepřímou indexací) a nadměrné synchronizaci.

Časová složitost¶

Paralelní čas se skládá z inicializace a paralelního výpočtu:

$T(n, range, p) = O(range) + O(n/p)$

Paralelní řešení (Efektivní přístup)¶

Rozdělte data na $p$ částí a spočítejte částečné histogramy pro každou část.
Proveďte paralelní redukci výsledků z jednotlivých lokálních histogramů.
Tento přístup je efektivní, protože nedochází k výpadkům cache.
Ve výchozím nastavení je rozdělení v paralelní smyčce blokové, což je ve OpenMP specifikováno jako schedule(static).

int *A, n;                 // vstupní pole a jeho velikost
int histogram[p][range];  // p = počet vláken

#pragma omp parallel
{
    int my_id = omp_get_thread_num();

    // Každé vlákno inicializuje svůj histogram postupně
    for (int i = 0; i < range; i++) {
        histogram[my_id][i] = 0;
    }

    // Výpočet histogramu
    #pragma omp for schedule(static)
    for (int j = 0; j < n; j++) {
        histogram[my_id][A[j]]++;
    }

    // Každé vlákno redukuje range/p p-tice lokálních čítačů
    #pragma omp for schedule(static)
    for (int i = 0; i < range; i++) {
        for (int j = 1; j < p; j++) {
            histogram[0][i] += histogram[j][i];
        }
    }
}

Časová složitost¶

Paralelní čas se skládá z inicializace, paralelního výpočtu a paralelní redukce:

$T(n, range, p) = O(range) + O(n/p) + O(range)$

12. Paralelizace násobení polynomů v OpenMP¶

Problém:¶

Máme dvě pole koeficientů polynomů o velikostech $m$ a $n$ , a chceme spočítat výstupní polynom.

Sekvenční algoritmus - Časová složitost: $O(n * m)$ ¶

Na začátku inicializujeme výstupní pole tak, že všechny prvky nastavíme na 0:

   for (int i = 0; i < n + m; i++) {
       result[i] = 0;
   }

Pro každý prvek v prvním poli vynásobíme každým prvkem ve druhém poli a přičteme výsledek do odpovídajícího indexu ve výstupním poli:

   for (int i = 0; i < n; i++) {
       for (int j = 0; j < m; j++) {
           result[i + j] += a[i] * b[j];
       }
   }

Tento přístup je nevhodný pro paralelizaci kvůli nepřímé indexaci.

Paralelní algoritmus – vnější cyklus $(i)$ - Časová složitost: $O(n * m / p)$ ¶

Použití #pragma omp parallel for na vnějším cyklu s atomic update.

   #pragma omp parallel for
   for (int i = 0; i < n; i++) {
       for (int j = 0; j < m; j++) {
           #pragma omp atomic
           result[i + j] += a[i] * b[j];
       }
   }

Opět dochází k nepřímé indexaci a výpadkům cache, takže tento přístup nebude efektivní.

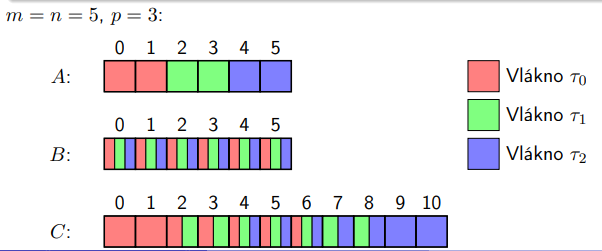
Pasted image 20230616122515.png

Paralelní algoritmus – vnitřní cyklus $(j)$ - Časová složitost: $O(n * m / p)$ ¶

Použití #pragma omp parallel for na vnitřním cyklu.

   #pragma omp parallel
   for (int i = 0; i < n; i++) {
       #pragma omp for schedule(static)
       for (int j = 0; j < m; j++) {
           result[i + j] += a[i] * b[j];
       }
   }

Dochází k zpomalení kvůli synchronizaci bariér po každé iteraci vnějšího cyklu.
Tento přístup již nevyužívá nepřímou indexaci, ale může dojít k falešnému sdílení.

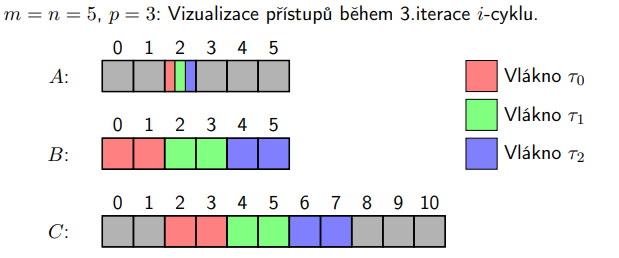
Pasted image 20230616122256.png

Paralelní algoritmus nad výstupem - Časová složitost: $O(n * m / p)$ ¶

Každé vlákno počítá část výstupních koeficientů, následně se provede paralelní redukce.

   #pragma omp parallel for schedule(static,chunk_size)
   for (/* určené rozsahy */) {
       // Výpočet části výstupních koeficientů
   }
   // Paralelní redukce

// A, B a C jsou polynomy, které budou násobeny.
// A má stupen m, B má stupen n a C bude mít stupen m+n.
int A[m+1], B[n+1], C[m+n+1];

// Získání počtu dostupných procesorů.
int p = omp_get_num_procs();

// Paralelní for smyčka, která iteruje přes všechny prvky výsledného
// polynomu C. Statické rozdělení iteračního prostoru je použito,
// kde každé vlákno zpracovává bloky o velikosti (m+n)/c*p.
// Hodnota 'c' je faktor, kterým lze upravit velikost bloku.
#pragma omp parallel for schedule(static,(m+n)/c*p)
for (int k = 0; k <= (m + n); k++) {

    // Vnitřní smyčka iteruje přes prvky, které je třeba násobit
    // a sčítat pro výpočet konkrétního prvku výsledného polynomu C.
    // Pro každé 'k', 'l' musí být mezi max(0, k - n) a min(k, m),
    // což odpovídá prvku, který je aktuálně počítán.
    for (int l = max(0, k - n); l <= min(k, m); l++) {

        // Přičte A[l]*B[k-l] k prvkům výsledného polynomu C[k].
        C[k] += A[l]*B[k-l];
    }
}

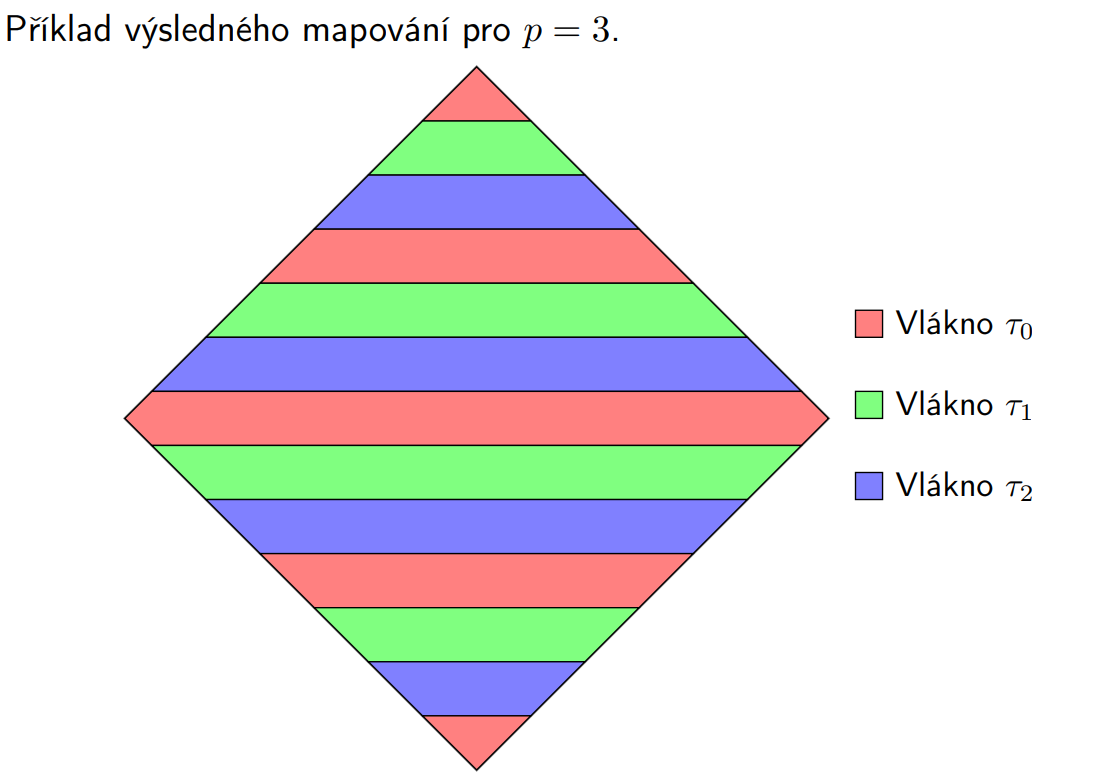
Například, koeficient u $x^2$ může být vypočítán jako $x^0 * x^2$ , $x^1 * x^1$ nebo $x^2 * x^0$ .
Je nutné vyvážit zátěž (dynamicky nebo staticky s vhodnou velikostí bloku).
Falešnému sdílení se dá vyhnout, pokud data vhodně rozdělíme s ohledem na velikost cache bloků.

Pasted image 20230620170332.png

13. Paralelizace násobení hustých matic (Matrix-Matrix Multiplication, MMM)¶

Problém:¶

Máme dvě matice $A$ a $B$ o rozměrech $n \cdot n$ a chceme vypočítat výslednou matici $C$ jako součin $A$ a $B$ .

Sekvenční algoritmus - Časová složitost: $O(n^3)$ ¶

Použijeme klasický školní algoritmus, kde pro každý index výsledné matice provedeme skalární součin příslušných řádků a sloupců.

for (int i = 0; i < n; i++) {
    for (int j = 0; j < n; j++) {
        double c = 0;
        for (int k = 0; k < n; k++) {
            c += A[i][k] * B[k][j];
        }
        result[i][j] = c;
    }
}

Paralelizace vnějšího cyklu $(i)$ - Časová složitost: $O(n^3 / p)$ ¶

Použijeme #pragma omp parallel for na vnějším cyklu.

#pragma omp parallel for
for (int i = 0; i < n; i++) {
    for (int j = 0; j < n; j++) {
        double c = 0;
        for (int k = 0; k < n; k++) {
            c += A[i][k] * B[k][j];
        }
        result[i][j] = c;
    }
}

Procesory se střídají v počítání jednotlivých řádků a zapisují do disjunktních oblastí paměti.
Minimální synchronizace (jen jedna bariéra na konci regionu), nedochází k falešnému sdílení.

Paralelizace vnitřního cyklu $(j)$ - Časová složitost: $O(n^3 / p)$ ¶

Použijeme #pragma omp parallel for s schedule(static) na vnitřním cyklu s proměnnou j.

for (int i = 0; i < n; i++) {
    #pragma omp parallel for schedule(static)
    for (int j = 0; j < n; j++) {
        double c = 0;
        for (int k = 0; k < n; k++) {
            c += A[i][k] * B[k][j];
        }
        result[i][j] = c;
    }
}

Procesory se střídají v počítání jednotlivých bloků a zapisují do disjunktních oblastí paměti.
Dochází k větší synchronizaci ( $n$ bariér). Pokud je $n/p$ dostatečně velké, nedojde k falešnému sdílení.
Pokud bychom data rozdělili cyklicky (schedule(static,1)), mohlo by dojít k falešnému sdílení.

Paralelizace vnitřního cyklu $(k)$ - Časová složitost: $O(n^3 / p)$ ¶

Použijeme #pragma omp parallel for na vnitřním cyklu s proměnnou k.

for (int i = 0; i < n; i++) {
    for (int j = 0; j < n; j++) {
        double c = 0;
        #pragma omp parallel for reduction(+:c)
        for (int k = 0; k < n; k++) {
            c += A[i][k] * B[k][j];
        }
        result[i][j] = c;
    }
}

Procesory pomocí paralelní redukce počítají jednotlivé hodnoty ve skalárním součinu.
Dochází k velké synchronizaci ( $n^2$ bariér), ale pouze jedno vlákno zapisuje do výsledku, což eliminuje kolize v cache.
Dále tam dochází k $n^2$ redukcím
Zatím největší režie synchronizace $n^2 ∗ (T_{barr} + T_{PR}(n, p))$
Všechna vlákna redundantně iterují identicky $i$ - a $j$ -cyklus

14. Formáty pro uložení řídkých matic a paralelizace násobení řídké matice vektorem (MVM) v OpenMP¶

Řídké matice¶

Řídká matice je matice, která má více nulových prvků než nenulových. Místo ukládání všech prvků, ukládáme v paměti pouze nenulové prvky a jejich souřadnice.

Každý prvek matice se po přenesení z hlavní paměti do registru použije pouze 1x,
Výkonnost je tedy limitovaná propustností rozhraní mezi CPU a hlavní pamětí.

Formáty pro uložení řídké matice¶

Souřadnicový formát (COO):
- Udržujeme tři pole - pole řádků (row_index), pole sloupců (col_index), a pole hodnot (element).
- Pro každé k od 0 do n: result[row_index[k]][col_index[k]] = element[k].

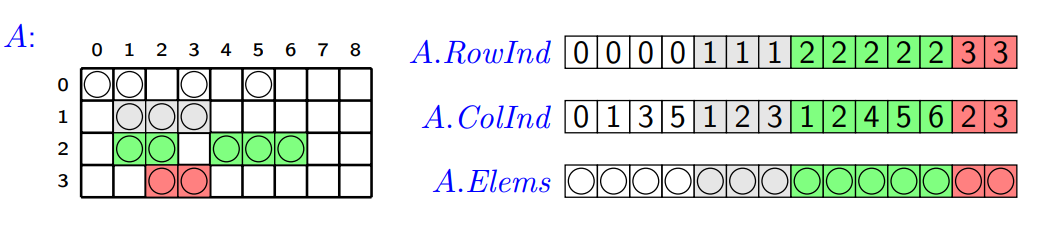
Pasted image 20230617162320.png

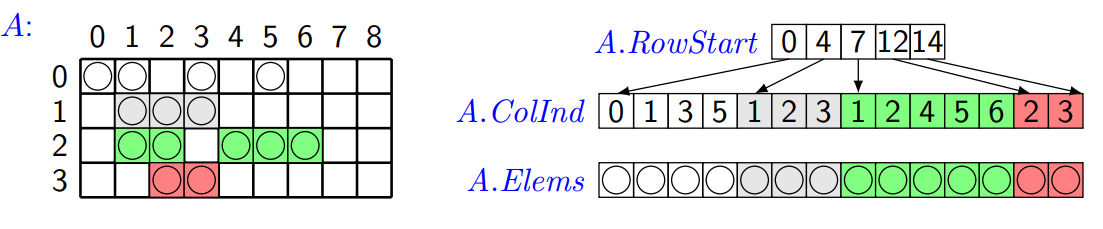
Formát komprimovaných řádků (CSR):
- Opět udržujeme tři pole – pole řádků (row_start), pole sloupců (col_index), a pole hodnot (element).
- Tentokrát ale pole řádků obsahuje indexy do pole col_index, kde začíná daný řádek.

Pasted image 20230617162344.png

Násobení řídké matice vektorem¶

Máme matici $A$ , vstupní vektor $x$ a výstupní vektor $y$ .

Sekvenční algoritmus - Časová složitost: $O(n)$ ¶

COO:

for (i = 0; i < n; i++} 
     y[i] = 0.0;

for (int k = 0; k < n; k++) {
    y[row_index[k]] += elements[k] * x[col_index[k]];
}

CSR:

for (int row = 0; row < row_count; row++) {
    double sum = 0;
    for (int k = row_start[row]; k < row_start[row + 1]; k++) {
        sum += elements[k] * x[col_index[k]];
    }
    y[row] = sum;
}

Paralelizace COO - Časová složitost: $O(n/p)$ ¶

Jak to funguje: V tomto přístupu, použijeme #pragma omp parallel for na cyklu a aktualizujeme výsledek atomicky. V praxi to znamená, že různá vlákna budou přistupovat k různým řádkům matice a přičítat výsledky.

#pragma omp parallel{
    #pragma omp for
    for (i = 0; i < n; i++) { 
        y[i] = 0.0;
    }
    #pragma omp parallel for
    for (int k = 0; k < n; k++) {
        #pragma omp atomic update
        y[row_index[k]] += elements[k] * x[col_index[k]];
    }
}

Nevýhody:
Kolize: Při aktualizaci výsledku může dojít ke kolizím, protože více vláken může současně přistupovat ke stejné paměti.
Falešné sdílení: Kód může trpět falešným sdílením cache kvůli paralelnímu přístupu k prvku pole, což vede k zbytečné synchronizaci a poklesu výkonu

Paralelizace CSR - Časová složitost: $O(n/p)$ ¶

Jak to funguje: V tomto případě můžeme také použít #pragma omp parallel for na vnější cyklus, aby jedno vlákno řešilo vždy n řádků.

#pragma omp parallel for 
for (int row = 0; row < row_count; row++) {
    double sum = 0;
    for (int k = row_start[row]; k < row_start[row + 1]; k++) {
        sum += elements[k] * x[col_index[k]];
    }
    y[row] = sum;
}

Statické rozdělení bloků: `schedule(static)`¶

Nevýhody:
Anomálie statického prohledávání: Pokud matice nemá rovnoměrně zaplněné řádky, vlákna mohou mít nerovnoměrnou výpočetní zátěž, což může snižovat celkový výkon.
Falešné sdílení: Kvůli anomálii statického prohledávání nelze zarovnat na bloky cache.

Dynamické rozdělení bloků: `schedule(dynamic)`¶

Nevýhody:
Falešné sdílení: Rozdělení může vést k falešnému sdílení.
Komunikační režie Dynamické rozdělení má větší režii než statické.

Balancované rozdělení bloků¶

Jak to funguje: Pro nerovnoměrně zaplněné řádky můžeme sloučit řádky do pruhů (bands) a paralelizovat přes tyto pruhy. Tedy každé vlákno bude mít přibližně stejný počet aritmetických operací.

Tohoto můžeme dosáhnout tak, že hodnota row_start[i+1] - row_start[i] nám poskytne počet prvků v jednom řádku.

// Pole 'band' obsahuje indexy prvních řádků v pásech přiřazených jednotlivým vláknům.
int band[p+1];
// Nastavení posledního prvku pole 'band' na 'n', což odpovídá počtu řádků matice.
band[p] = n;

// Vytvoření paralelního bloku, ve kterém vlákna provádí své výpočty.
#pragma omp parallel
{
    // Získání identifikátoru vlákna.
    int my_id = omp_get_thread_num();

    // Výpočet ideálního indexu prvního nenulového prvku v matici 'A.Elems' pro dané vlákno.
    // N je celkový počet nenulových prvků v matici a p je počet vláken.
    int my_number = my_id * N / p;

    // Provedení binárního vyhledávání v poli 'A.RowStart' k nalezení indexu řádku,
    // kde se nachází prvek odpovídající hodnotě 'my_number'.
    int my_index = binary_search(A.RowStart, my_number);

    // Uložení indexu prvního řádku pásma, které bude zpracováváno tímto vláknem.
    band[my_id] = my_index;

    // Synchronizace všech vláken - zajistí, že matice 'A' je rozdělena na 'p' pásem
    // před pokračováním dalších výpočtů.
    #pragma omp barrier

    // Iterace přes řádky v pásmu přiřazeném tomuto vláknu.
    for (int i = band[my_id]; i < band[my_id + 1]; i++) {

        // Inicializace proměnné pro součet prvků řádku.
        double sum = 0.0;

        // Iterace přes nenulové prvky daného řádku matice 'A'.
        // Výpočet skalárního součinu řádku s vektorem 'x'.
        for (int k = A.RowStart[i]; k < A.RowStart[i + 1]; k++) {
            sum += A.Elems[k] * x[A.ColInd[k]];
        }

        // Uložení výsledku skalárního součinu do výsledného vektoru 'y'.
        y[i] = sum;
    }
}

Výhody:
Efektivní i pro nerovnoměrně zaplněné matice.
Nevýhody:
Složitější implementace.

4. Základní paralelní algoritmy

11. Paralelizace výpočtu histogramu pomocí OpenMP¶

Standardní algoritmus – Časová složitost: O(n) + O(range)O(n) + O(range)¶

Paralelní řešení (Naivní přístup)¶

Časová složitost¶

Paralelní řešení (Efektivní přístup)¶

Časová složitost¶

12. Paralelizace násobení polynomů v OpenMP¶

Problém:¶

Sekvenční algoritmus - Časová složitost: O(n * m)O(n * m)¶

Paralelní algoritmus – vnější cyklus (i)(i) - Časová složitost: O(n * m / p)O(n * m / p)¶

Paralelní algoritmus – vnitřní cyklus (j)(j) - Časová složitost: O(n * m / p)O(n * m / p)¶

Paralelní algoritmus nad výstupem - Časová složitost: O(n * m / p)O(n * m / p)¶

13. Paralelizace násobení hustých matic (Matrix-Matrix Multiplication, MMM)¶

Problém:¶

Sekvenční algoritmus - Časová složitost: O(n^3)O(n^3)¶

Paralelizace vnějšího cyklu (i)(i) - Časová složitost: O(n^3 / p)O(n^3 / p)¶

Paralelizace vnitřního cyklu (j)(j) - Časová složitost: O(n^3 / p)O(n^3 / p)¶

Paralelizace vnitřního cyklu (k)(k) - Časová složitost: O(n^3 / p)O(n^3 / p)¶

14. Formáty pro uložení řídkých matic a paralelizace násobení řídké matice vektorem (MVM) v OpenMP¶

Řídké matice¶

Formáty pro uložení řídké matice¶

Násobení řídké matice vektorem¶

Sekvenční algoritmus - Časová složitost: O(n)O(n)¶

Paralelizace COO - Časová složitost: O(n/p)O(n/p)¶

Paralelizace CSR - Časová složitost: O(n/p)O(n/p)¶

Statické rozdělení bloků: schedule(static)¶

Dynamické rozdělení bloků: schedule(dynamic)¶

Balancované rozdělení bloků¶

Standardní algoritmus – Časová složitost: $O(n) + O(range)$ ¶

Sekvenční algoritmus - Časová složitost: $O(n * m)$ ¶

Paralelní algoritmus – vnější cyklus $(i)$ - Časová složitost: $O(n * m / p)$ ¶

Paralelní algoritmus – vnitřní cyklus $(j)$ - Časová složitost: $O(n * m / p)$ ¶

Paralelní algoritmus nad výstupem - Časová složitost: $O(n * m / p)$ ¶

Sekvenční algoritmus - Časová složitost: $O(n^3)$ ¶

Paralelizace vnějšího cyklu $(i)$ - Časová složitost: $O(n^3 / p)$ ¶

Paralelizace vnitřního cyklu $(j)$ - Časová složitost: $O(n^3 / p)$ ¶

Paralelizace vnitřního cyklu $(k)$ - Časová složitost: $O(n^3 / p)$ ¶

Sekvenční algoritmus - Časová složitost: $O(n)$ ¶

Paralelizace COO - Časová složitost: $O(n/p)$ ¶

Paralelizace CSR - Časová složitost: $O(n/p)$ ¶

Statické rozdělení bloků: `schedule(static)`¶

Dynamické rozdělení bloků: `schedule(dynamic)`¶