5. Pokročilé paralelní algoritmy

15. Základní Principy Paralelizace QuickSortu a Paralelního Rozdělení v OpenMP¶

QuickSort je algoritmus řazení s průměrnou časovou složitostí $O(n\cdot log(n))$ . Funguje tak, že vybere 'pivot' prvek a rozdělí pole na dvě podpole, takže prvky menší než pivot jsou před ním a prvky větší než pivot za ním. Tato podpole jsou pak rekurzivně seřazena.

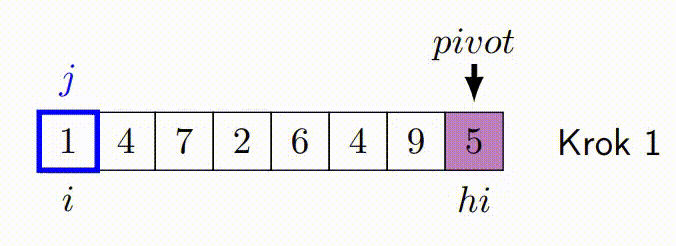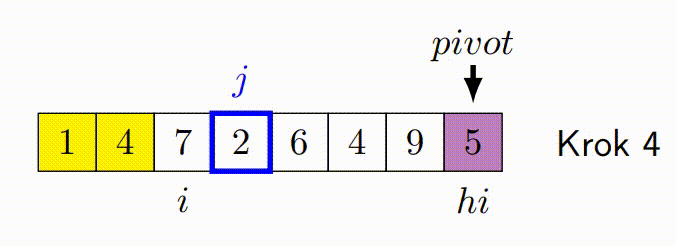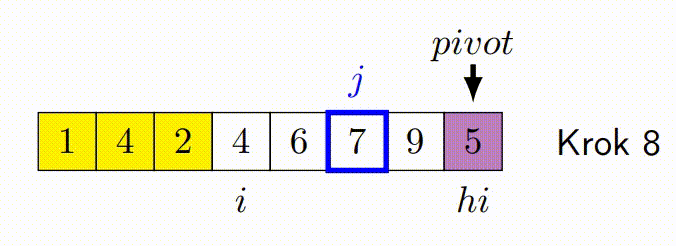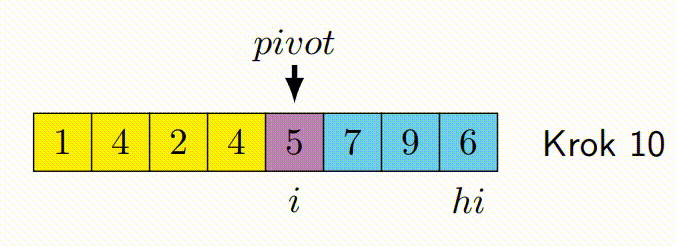
Recording 2023-06-20 180043.gif

Základní Paralelizace Pomocí Úloh - $O(n * log(n) / p)$ ¶

Základní myšlenka paralelizace QuickSortu spočívá v provádění rekurzivních volání na levé a pravé části paralelně.
Toho lze dosáhnout pomocí OpenMP direktivy #pragma omp task pro levou a pravou část.

Avšak tato naivní metoda může být pomalá kvůli režii vytváření úloh a čekání na dokončení podvláken.

void parallel_quicksort(int* arr, long low, long high) {
    #pragma omp parallel // Create a team of threads
    {
        #pragma omp single // Only a single thread executes the recursive calls
        {
            parallel_quicksort_recursive(arr, low, high);
        }
    }
}

void parallel_quicksort_recursive(int* arr, long low, long high) {
    if (low < high) {
        long pivotIndex = partition(arr, low, high); 

        #pragma omp task // Recursive call as a separate task, can be executed by different threads
        parallel_quicksort_recursive(arr, low, pivotIndex - 1);

        #pragma omp task // Recursive call as a separate task, can be executed by different threads
        parallel_quicksort_recursive(arr, pivotIndex + 1, high);
    }
}

Vylepšená Paralelizace Pomocí Úloh¶

Prah počtu úloh: Použijte direktivu #pragma omp task if(depth < DEPTH_THRESHOLD) k nastavení prahu pro hloubku rekurze, do které by měly být vytvářeny úlohy.
Nahrazení jednoho z rekurzivních volání iterací: Tímto lze snížit počet vytvořených úloh na polovinu.
Vyvažování Zátěže: Rozdělte vlákna mezi levé a pravé části podle jejich velikosti.

Paralelní Rozdělení: Kromě paralelního řazení také paralelizujte fázi rozdělení.

const int DEPTH_THRESHOLD = 4;

void parallel_quicksort(int* arr, long low, long high) {
    #pragma omp parallel // Create a team of threads
    {
        #pragma omp single // Only a single thread executes the recursive calls
            par_quicksort_rec(arr, low, high, 0);
    }
}

void par_quicksort_rec(int* arr, long low, long high, int depth) {
    while (low < high) {
        long pivotIndex = partition(arr, low, high); 

        #pragma omp task if (depth < DEPTH_THRESHOLD) // Limit the depth of recursion for task creation
        par_quicksort_rec(arr, low, pivotIndex - 1, depth + 1);

        // Using iteration instead of recursion for the right part
        depth += 1
        low = pivotIndex + 1;
    }
}

Hoareuv QuickSort¶

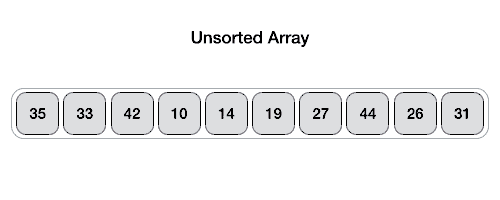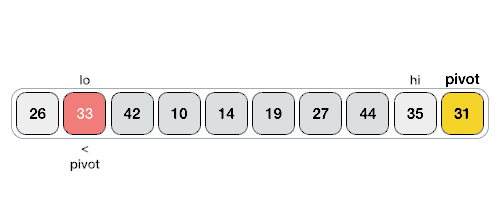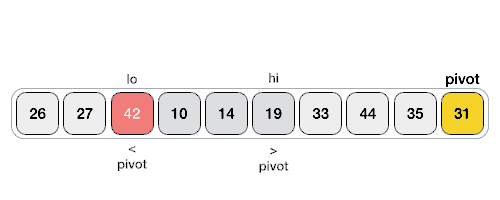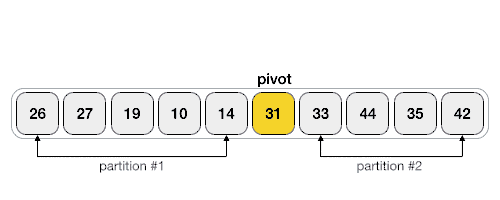
Vybere pivotní prvek, často první nebo poslední prvek v podpoli.
Má dva ukazatele - jeden na začátku pole a druhý na konci.
Ukazatele se pohybují proti sobě. Levý ukazatel postupuje doprava, dokud nenajde prvek větší než pivot. Pravý ukazatel postupuje doleva, dokud nenajde prvek menší než pivot.
Pokud se ukazatele ještě nepřekřížily, prohodí nalezené prvky a pokračují v krocích 3 a 4.
Proces končí, když se ukazatele překříží. Pole je pak rozděleno na dva segmenty, prvky menší než pivot a prvky větší než pivot.

hoaer quick sort.gif

Paralelní Rozdělení pomoci Hoareova QuickSortu¶

Tento algoritmus vyžaduje aktivovaný vnořený (= nested) OpenMP paralelizmus
- Tedy v paralelním regionu, který provádí sekvenčně $P$ vláken najednou, se jedno vlákno může opět rozdělit na více vláken.
- Zavolá se: omp_set_nested(1); coz zapne vnořený paralelizmus

Níže uvedený kód ukazuje, že Hoareův quicksort se liší pouze výpočtem partition který je nyní paralelizovatelný.

const int DEPTH_THRESHOLD = 4;

void parallel_quicksort(int* arr, long low, long high) {
    omp_set_nested(1); //1 = true
    #pragma omp parallel // Create a team of threads
    {
        #pragma omp single // Only a single thread executes the recursive calls
            par_quicksort_rec(arr, low, high, 0);
    }
}

void par_quicksort_rec(int* arr, long low, long high, int depth) {
    while (low < high) {
        long r = par_partition(A, lo, hi); //nested parallelism

        #pragma omp task if (depth < DEPTH_THRESHOLD) // Limit the depth of recursion for task creation
        par_quicksort_rec(arr, low, pivotIndex - 1, depth + 1);

        // Using iteration instead of recursion for the right part
        depth += 1
        low = pivotIndex + 1;
    }
}

Hoareho Paralelní Algoritmus Rozdělení¶

Máme dva ukazatele, které se pohybují proti sobě.
Pozice těchto ukazatelů lze upravit pomocí #pragma omp atomic capture.
Na konci mohou zůstat „špinavá čísla“ (prvky v nesprávné části), která je potřeba přehodit sekvenčně.
Maximálně můžu získat $p$ špinavých bloků, tedy tolik špinavých bloků, kolik je počet vláken.
Nakonec projedu pole sekvenčně, abych opravil špinavé bloky.
Nevyhody:
- Vysoký Počet Synchronizačních Operací
- False sharing
- Vyvažování Zátěže

hoare paralel bad.gif

Vylepšený Paralelní Algoritmus Rozdělení v Hoareově QuickSortu¶

Vylepšený paralelní algoritmus rozdělení v Hoareově QuickSortu se zaměřuje na efektivní paralelizaci fáze rozdělení. Tato fáze je kritická, protože určuje, jak se prvky rozdělí kolem vybraného pivotu. Vylepšená verze se snaží minimalizovat počet špinavých bloků a maximalizovat efektivitu paralelního zpracování.

Následující kroky popisují, jak vylepšený paralelní algoritmus rozdělení funguje:

Inicializace: V algoritmu se vybere pivot, podobně jako v klasickém Hoareově algoritmu. Algoritmus také inicializuje ukazatele, které budou procházet polem od obou konců. Na rozdíl od klasického přístupu, vylepšená verze rozdělí data do bloků, které budou zpracovávány paralelně.
Paralelní Zpracování Bloků: Každé vlákno zpracovává blok prvků a porovnává je s pivotem. Podle porovnání zařadí prvky za sebe, tj. prvky menší než pivot umisťuje na jednu stranu a prvky větší než pivot na druhou stranu ve svém bloku. Důležité je, že každý blok je zpracováván sekvenčně a nejsou zde použity žádné zámky, což minimalizuje režii synchronizace.
Pohyb Ukazatelů a Kontinuální Zpracování Bloků: Základní myšlenka s ukazateli zůstává stejná jako v klasickém Hoareově algoritmu, ale místo přepínání vláken po každém prvku se ukazatele pohybují po zpracovaných blocích. Pokud je zpracován levý blok, ukazatel vezme další levý blok a pokračuje v jeho zpracování zatimco pravy blok pokracuje tam kde zkoncil. Tento princip platí i naopak pro pravý ukazatel. Tato technika snižuje počet nutných synchronizačních operací mezi vlákny a zlepšuje výkon.
Oprava Špinavých Bloků: Po dokončení paralelního kroku mohou existovat $p$ špinavých bloků, což jsou bloky, které obsahují prvky, které ještě nebyly správně rozděleny (některé by mohly být menší a jiné větší než pivot). Tento krok spočívá v sekvenčním seřazení těchto špinavých bloků, aby bylo zajištěno, že pole je správně rozděleno kolem pivotu.

Tímto způsobem, vylepšený paralelní algoritmus rozdělení může efektivně využívat paralelní zpracování, zejména pro velké datasety, a minimalizovat počet synchronizačních operací a špinavých bloků.

Nevyhody:
- Vyvažování Zátěže

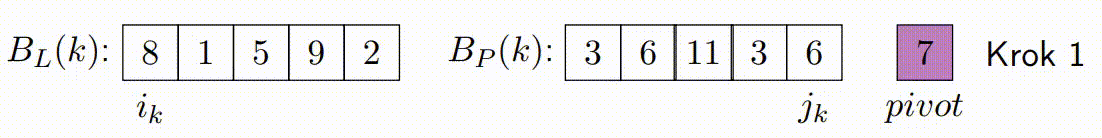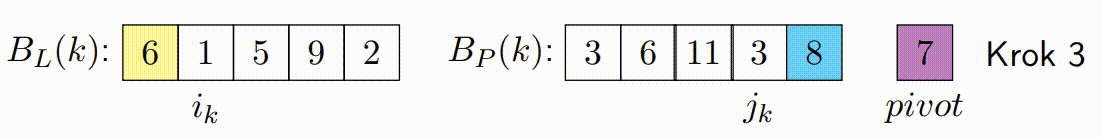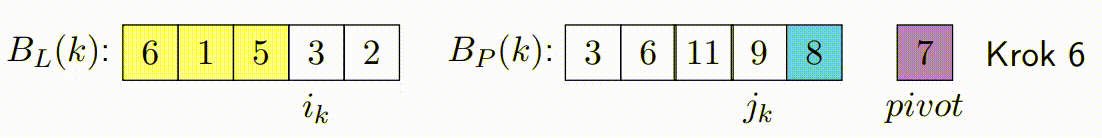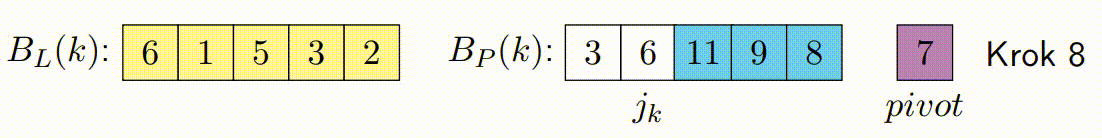
hoare paralel good.gif

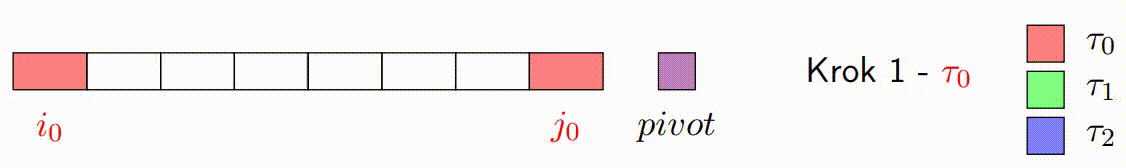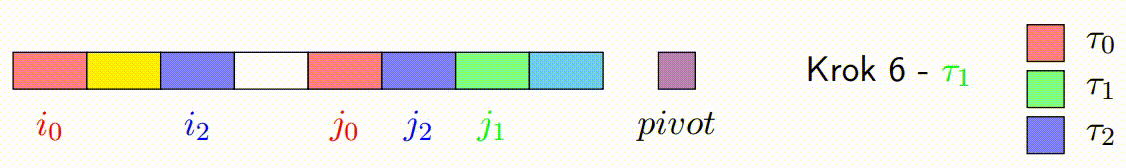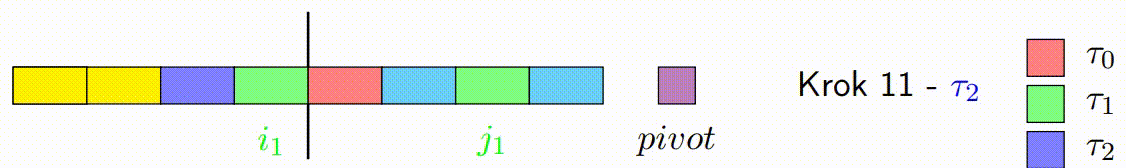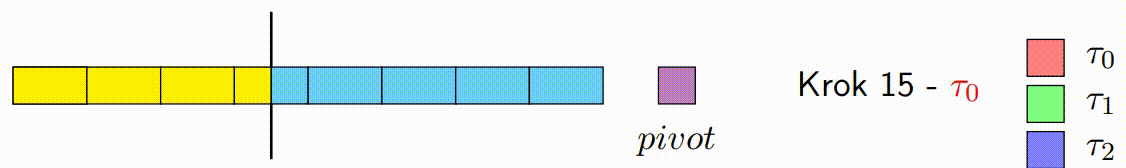
hoare paralel good overview.gif

const long K = ...; // Definujte hodnotu K

long par_partition_block(int* A, long lo, long hi) {
    long pivot = A[hi];
    long i = lo;
    long j = hi - 1;

    #pragma omp parallel
    {
        long my_i, my_j, init_my_i, init_my_j;

        #pragma omp atomic capture
        {
            my_i = i;
            i += K;
        }

        #pragma omp atomic capture
        {
            my_j = j;
            j -= K;
        }

        init_my_i = my_i;
        init_my_j = my_j;

        while (my_i < my_j) {
            // Předpokládám, že funkce 'neutralizace' je někde definována
            neutralizace(A, my_i, init_my_i, my_j, init_my_j, K, pivot);

            if (my_i >= init_my_i + K) {
                #pragma omp atomic capture
                {
                    my_i = i;
                    i += K;
                }
                init_my_i = my_i;
            }

            if (my_j <= init_my_j - K) {
                #pragma omp atomic capture
                {
                    my_j = j;
                    j -= K;
                }
                init_my_j = my_j;
            }
        }

        #pragma omp barrier

        // ...neutralizace max. p zbývajících bloků
    }

    // ...úklid posledního špinavého bloku

    return j; //vrácení indexu hranice mezi levým a pravým segmentem
}

Vyvažování¶

Paralelní rozdělování (neutralizace) je hlavní výpočetní složkou QuickSortu, zbytek je nastavování ukazatelů a krátký epilog.
QuickSort je datově citlivý: Poměr velikosti levé a pravé části pro další úroveň rekurze závisí na kvalitě výběru pivota.
Je-li např. poměr velikosti levé a pravé části 2:5, bylo by ideální přidělit vlákna pro provádění vnořených paralelních regionů (klauzulí num_threads direktivy#pragma omp parallel) paralelního rozdělení přibližně v takovém poměru.
Každé z obou částí je ale současně třeba přidělit aspoň 1 vlákno, ať je ta část sebekratší (třeba 5 čísel).

16. Základní myšlenky paralelizace MergeSortu a paralelního dvoucestného sloučení v OpenMP¶

MergeSort¶

Merge Sort, neboli algoritmus řazení sléváním, je jeden z klasických algoritmů pro řazení dat. Merge sort pracuje na principu "rozlož a panuj".

Nejprve rekurzivně rozděluje pole až na jednotlivé prvky, poté postupně slučuje sousední podpole, přičemž je seřazuje. Tento proces pokračuje, dokud nejsou všechna podpole spojena do jednoho seřazeného celku.

Základní Princip: - Rozdělení pole na dvě menší podčásti - Seřazení těchto podčástí - Sloučení těchto dvou seřazených polí do jednoho seřazeného pole

Základní Task Paralelizace¶

Zde využijeme OpenMP k vytvoření úloh (tasks) pro levou a pravou část pole.

#pragma omp task
// recursive call to sort the left part

#pragma omp task
// recursive call to sort the right part

#pragma omp taskwait
// merge the sorted parts

Problém: Pokud rozdělíme pole na příliš mnoho malých částí, vznikne falešné sdílení (false sharing) a vysoká režie pro správu úloh, což degraduje výkon.

Vylepšená Task Paralelizace¶

Prah počtu úloh: Použití podmínky pro omezení hloubky rekurze.

#pragma omp task if(depth < DEPTH_THRESHOLD)

Snížení počtu úloh: Nahrazení jednoho rekurzivního volání iterací. To snižuje počet úloh na polovinu.
Paralelizace slučovací operace: Kromě paralelního řazení je také možné paralelizovat slučovací operaci. To zrychluje celkový proces.

Paralelní Dvoucestné Slučování¶

Paralelní dvoucestné slučování je technika optimalizace slučovací fáze Merge Sort algoritmu, když pracujeme s více procesorovými vlákny.

Krok 1: Vytvoření Matice Přechodů¶

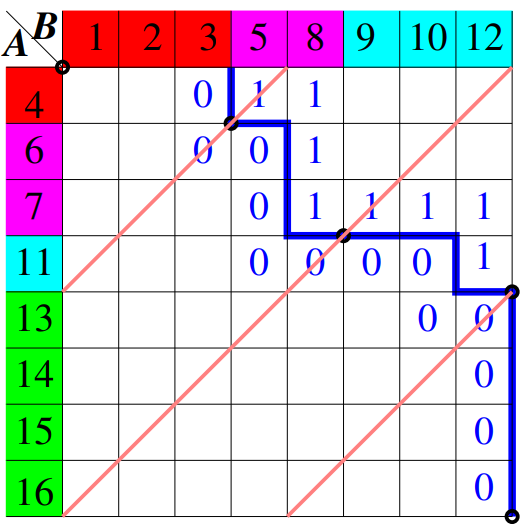
Máme dvě seřazená pole, A a B. Naším cílem je sloučit tato dvě pole do jednoho seřazeného pole C. Nejprve si sekvenčně vytvoříme matici X, kde každý prvek $X[i][j]$ je 0, pokud $A[i] > B[j]$ , a 1 v opačném případě. Protože pole jsou seřazená, bude existovat přechod mezi hodnotami 0 a 1 v této matici.

Krok 2: Diagonální Proložení¶

Nyní chceme rozdělit práci mezi více vlákny. K tomu použijeme techniku nazývanou diagonální proložení. Proložíme matici X s $(p-1)$ vedlejšími diagonálami, kde $p$ je počet vláken, které chceme použít. Tyto diagonály jsou ekvidistantní a rozdělují matici do bloků.

Krok 3: Výpočet Průsečíků¶

Pro každou diagonálu potřebujeme najít průsečík s přechodem mezi hodnotami 0 a 1 v matici. To nám pomůže určit, jaká část pole A a B by měla být sloučena daným vláknem. Průsečíky lze najít pomocí binárního půlení, což je efektivní metoda s časovou složitostí $O(\log n)$ .

Pasted image 20230616124452.png

Krok 4: Sloučení Bloků¶

Nyní každé vlákno provede slučovací operaci sekvenčně na svých přidělených blocích. To znamená, že vlákno $i$ sloučí bloky $A_i$ a $B_i$ na základě vypočtených průsečíků.

Krok 5: Spojení Výsledků¶

Na konci, po dokončení slučovací operace ve všech vláknech, spojíme výsledné bloky od všech vláken k vytvoření finálního seřazeného pole C.

Ačkoliv paralelní dvoucestné slučování může výrazně zvýšit rychlost, může docházet k falešnému sdílení, což znamená, že více vláken může současně přistupovat k datům, která jsou blízko sebe v paměti. To může způsobit, že vlákna si navzájem přepisují data a může dojít k poklesu výkonu. V takových případech může být užitečné použít alternativní techniky jako například p-cestné paralelní slučování.

17. Základní myšlenky paralelního p-cestného MergeSortu v OpenMP¶

Úvod¶

Paralelní p-cestne slucovani v MergeSortu je varianta klasického MergeSort algoritmu, která efektivně rozděluje práci na slucovani mezi více vlákny.

Paralelní p-cestný MergeSort¶

Krok 1: Rozdělení dat na podčásti¶

Příprava: Máme vstupní pole $S$ o velikosti $n$ a chceme ho rozdělit na $p$ podpolí, kde $p$ je počet dostupných vláken. Každé podpole bude mít velikost přibližně $n/p$ .
Rozdělení: To znamená, že rozdělíme pole $S$ na menší podpolí $S[0], S[1], ..., S[p-1]$ .

Krok 2: Seřazení podčástí¶

Paralelní seřazení: Každé vlákno je zodpovědné za seřazení jednoho z podpolí. To znamená, že vlákno $i$ bude seřazovat podpole $S[i]$ .
Potom nasleduje bariera.

Krok 3: Výpočet oddělovačů¶

Určení oddělovačů: Po seřazení podčástí potřebujeme určit oddelovace. Každé vlákno potrebuje najit takovy oddelovac ktery kdyz aplikuje na serazene podcasti tak ten pivot bude odelovat cisla tak aby pred pivotem bylo $\text{id} * (n/p)$ cisel.
Význam oddělovačů: Oddělovače nám pomohou určit, jaké části různých podpolí se mají sloučit do jednoho kontinuálního seřazeného segmentu.

Krok 4: Sloučení úseků¶

Paralelní sloučení: Vlákna nyní začnou slučovat části, které jim byly přiděleny na základě oddělovačů. To je provedeno tak, že každé vlákno sloučí své příslušné úseky do jednoho kontinuálního seřazeného segmentu .
Slučovací algoritmus: Slučování může být provedeno pomocí standardního sekvencniho slučovacího algoritmu, který spojuje p seřazenych seznamu do jednoho seřazeného seznamu.

Pasted image 20230616125305.png

Krok 5: Konečná synchronizace¶

Po dokončení slučovacích operací všech vláken, budeme mít $p$ seřazených segmentů. Tyto segmenty potom můžeme ještě jednou sloučit do jednoho výsledného seřazeného pole.
Je důležité zajistit, že vlákna jsou synchronizovaná před tímto krokem, aby se zabránilo jakýmkoli problémům s přístupem k datům.

Poznámka: Po seřazení jednotlivých částí a výpočtu oddělovačů musí být bariéry, aby bylo zajištěno, že všechna vlákna dokončila svou práci předtím, než se začne sloučování.

#pragma omp parallel num_threads(NUM_THREADS)
{
    // Rozdělení a seřazení podčástí
    // ...

    #pragma omp barrier  // Synchronizace vláken

    // Výpočet oddělovačů
    // ...

    #pragma omp barrier  // Synchronizace vláken

   // Sloučení úseků
   // ...
}

// Konečná synchronizace a slučování segmentů

Asymptotický Odhad Paralelního Času¶

Asymptotický odhad paralelního času T(p, n) je:

$T(p, n) = \Theta\left(\frac{n}{p} \log \left(\frac{n}{p}\right) + \log(n) \cdot p \cdot\log \left(\frac{n}{p}\right) + \frac{n}{p} \log (p)\right)$

První část vyjadřuje sekvenční řazení $\frac{n}{p}$ čísel.
Druhá část je čas potřebný pro $log(n)$ provedení $p$ hledání v polích velikosti $\frac{n}{p}$ .
Třetí část je sekvenční p-cestné slučování $p$ polí celkové délky $\frac{n}{p}$ .