Semestrální projekt NI-PDP 2022/2023

Patrik Maly Magisterské studium, FIT CVUT, Thákurova 9, 160 00 Praha 6 May 11, 2023

Osah

• Osah
• Úloha MRO: Minimální hranový řez hranově ohodnoceného grafu
  • Vstupní data:
  • Úkol
• Definice problemu a popis sekvencniho algoritmu
  • Algoritmus
  • Výstup
  • Odchylky od zadání a důležité prvky
• Popis paralelního algoritmu a jeho implementace v OpenMP - táskovy paralelismus
  • Algoritmus
  • Výstup
• Popis paralelniho algoritmu a jeho implementace v OpenMP - datovy paralelismus
  • Algoritmus
  • Výstup
• Popis paralelniho algoritmu a jeho implementace v MPI
  • Algoritmus
    • Master
    • Slave
    • Serializace a deserializace dat
      • Vector
      • Map
  • Výstup
• Měření výsledků a vyhodnocení
• Manuálová stránka pro příkazovou řádku
• Závěr
• Literatura

Úloha MRO: Minimální hranový řez hranově ohodnoceného grafu

Vstupní data:

$n$= přirozené číslo představující počet uzlů grafu $G:150>n\ge10$ $k$ = přirozené číslo představující průměrný stupeň uzlu grafu $G: (3n/4) > k \ge 5$ $G(V,E)$ = jednoduchý souvislý neorientovaný hranově ohodnocený graf o $n$ uzlech a průměrném stupni $k$, váhy hran jsou z intervalu $<80,120>$
$a$ = přirozené číslo, $5 =< a =< n/2$

Úkol

Nalezněte rozdělení množiny uzlů $V$ do dvou disjunktních podmnožin $X, Y$ tak, že množina $X$ obsahuje $a$ uzlů, množina $Y$ obsahuje $n-a$ uzlů a součet ohodnocení všech hran {$u,v$} takových, že $u$ je z $X$ a $v$ je z $Y$ (čili velikost hranového řezu mezi $X$ a $Y$), je minimální.

Definice problemu a popis sekvencniho algoritmu

Algoritmus

Algoritmus SequentialAlgorithm řeší problém nalezení minimálního hranového řezu hranově ohodnoceného grafu. Toho dosahuje metodou prohledávání do hloubky (DFS) s ořezáváním. Tento přístup je známý jako metoda "Branch and Bound".

Algoritmus začíná s prázdnými množinami uzlů X a Y. V každém kroku rekurze se zkouší přidání aktuálního uzlu buď do množiny X nebo Y, dokud nejsou všechny uzly přiřazeny. Pro každé takové přiřazení algoritmus vypočítá cenu řezu a pokud je tato cena menší než dosud nejlepší nalezená cena, pak se toto rozdělení uzlů uchová jako aktuálně nejlepší řešení.

Výpočet ceny řezu a další klíčové operace jsou realizovány prostřednictvím tří hlavních funkcí: cutPrice(), cutPriceSimulate() a lowerBoundCutPrice().

Funkce cutPrice() vrací cenu řezu pro dané rozdělení uzlů grafu. Prochází všechny hrany grafu a pro každou hranu zjišťuje třídu (X, Y nebo NONE) obou uzlů na konci hrany. Pokud oba uzly patří do různých tříd a ani jeden z nich není třídy NONE, pak se cena hrany přičte k celkové ceně řezu.

Funkce cutPriceSimulate() simuluje cenu řezu, pokud by byl daný uzel přesunut do specifikované třídy. Nejprve získá aktuální třídu uzlu, pak dočasně změní třídu uzlu na specifikovanou třídu a vypočítá simulovanou cenu řezu. Po výpočtu vrátí uzel do jeho původní třídy a vrátí simulovanou cenu řezu.

Funkce lowerBoundCutPrice() odhaduje nejnižší možnou cenu zbývajícího řezu. Prochází všechny uzly grafu a pro ty, které ještě nebyly přiřazeny do žádné třídy (tj. jejich třída je NONE), simuluje cenu řezu pro obě možné třídy (X a Y) a přičte nižší z těchto dvou cen k odhadované ceně zbývajícího řezu. Je důležité poznamenat, že od simulovaných cen je odečtena základní cena řezu, což znamená, že funkce v podstatě odhaduje přidanou hodnotu, kterou by daný uzel přinesl k celkové ceně řezu, pokud by byl přidán do jedné z množin X nebo Y.

Tato metoda ořezávání založená na odhadu dolní hranice ceny řezu pomáhá značně zrychlit proces hledání řešení tím, že efektivně eliminuje mnoho neperspektivních cest v prostoru možných řešení. Pokud je dolní hranice ceny řezu pro dané částečné rozdělení uzlů vyšší než aktuálně nejlepší nalezená cena řezu, pak není nutné dále prozkoumávat tuto cestu, protože nemůže vést k lepšímu řešení.

Na konci výpočtu, pokud jsou v grafu stále uzly, které nebyly přiřazeny do množiny X nebo Y, jsou automaticky přiřazeny do množiny Y. Toto je provedeno na základě předpokladu, že pokud uzel nebyl explicitně zařazen do množiny X během procesu hledání řešení, pak by měl být zařazen do množiny Y.

Výstupem algoritmu je optimální rozdělení uzlů grafu do dvou množin tak, aby byla cena řezu mezi nimi byla minimální. Toto rozdělení je reprezentováno mapou, kde klíče jsou uzly a hodnoty jsou třídy uzlů (X nebo Y). Cena tohoto optimálního řezu je také vypočítána a uložena do proměné globalMinCut

Výstup

Výstupem algoritmu je mapa uzlů na jejich třídy (X nebo Y), která reprezentuje optimální řez. Vysednou cenu lze získat pomoci metody getResultCutPrice(). Kromě toho může být vygenerován diagram výsledného grafu ve formátu PlantUML pomocí metody plantUmlResultGraph().

Odchylky od zadání a důležité prvky

Tento algoritmus neobsahuje žádné zvláštní odchylky od zadání.

Popis paralelního algoritmu a jeho implementace v OpenMP - táskovy paralelismus

Algoritmus

Třída TaskParallelismAlgorithm je odvozená od základní třídy Algorithm. Tato třída implementuje metodu solve, která rozděluje uzly grafu do dvou skupin (X a Y) za účelem minimalizace ceny řezu. Na rozdíl od sekvenčního algoritmu, TaskParallelismAlgorithm využívá knihovnu OpenMP k paralelnímu zpracování a tím zrychlení výpočtu.

Funkce bbDfsSolve je velmi podobná svému protějšku v sekvenčním algoritmu, ale s jednou důležitou odlišností: je upravena pro paralelní zpracování pomocí direktiv OpenMP. Tato funkce provádí prohledávání do hloubky (DFS) s technikou branch and bound, ale nyní jsou obě větve prozkoumávání (pro přiřazení uzlu do skupiny X nebo Y) zpracovávány paralelně pomocí OpenMP tasků.

Konkrétně, #pragma omp task direktiva je použita pro vytvoření nové úlohy, která může být zpracována paralelně s jinými úlohami. Takto jsou vytvořeny dvě úlohy: jedna pro přiřazení aktuálního uzlu do skupiny X a druhá pro přiřazení do skupiny Y. Tyto úlohy jsou poté prováděny paralelně.

Pokud jde o funkci cutPrice, zůstává stejná jako v původním sekvenčním algoritmu.

Je důležité poznamenat, že přestože je použit paralelní přístup, výsledky algoritmu zůstávají stejné.

Celkově lze říci, že hlavní odlišností TaskParallelismAlgorithm od sekvenčního algoritmu je jeho schopnost zpracovávat výpočty paralelně, což může vést k výraznému zrychlení výpočtu, zejména pro velké grafy. Nicméně, paralelní zpracování vyžaduje pečlivé řízení souběžného přístupu k sdíleným datům, aby byla zajištěna správnost výsledků.

V této souvislosti stojí za povšimnutí, že kritická sekce kódu, která aktualizuje globální minimální cenu řezu a ukládá aktuální nejlepší rozdělení uzlů, je chráněna pomocí direktivy #pragma omp critical. Tato direktiva zajišťuje, že daný blok kódu může být v daném okamžiku vykonáván pouze jedním vláknem. To předchází možným problémům souběžného přístupu, jako jsou race conditions.

Funkce solve inicializuje výpočet a řídí jeho průběh. Na rozdíl od sekvenčního algoritmu, tato funkce využívá paralelní zpracování k výpočtu různých cest prohledávání grafu současně. To je dosaženo pomocí OpenMP direktiv #pragma omp parallel a #pragma omp single, které společně zajišťují, že funkce bbDfsSolve je spuštěna pouze jednou, ale může generovat mnoho paralelních úloh, které jsou poté zpracovány různými vlákny.

Konečně, konstruktor TaskParallelismAlgorithm zůstává stejný jako u původního algoritmu. Jediným rozdílem je přidání parametru numberOfThreads, který určuje počet vláken, které budou použity pro paralelní zpracování.

Ve výsledku, TaskParallelismAlgorithm poskytuje efektivní paralelní řešení pro problém minimálního řezu hran v grafu, aniž by se muselo významně měnit původní sekvenční řešení.

Výstup

Výstup algoritmu je stejný jako u sekvenčního algoritmu.

Popis paralelniho algoritmu a jeho implementace v OpenMP - datovy paralelismus

Algoritmus

Tento algoritmus pro výpočet minimálního řezu v grafu pomocí paralelního zpracování se od sekvenčního řešení liší v několika klíčových aspektech.

1. Předvýpočet možných řešení: Funkce fillPossibleSolutions vytváří množství potenciálních řešení, které je třeba prozkoumat, na základě zadané hloubky průchodu grafem bfsDepth. Toto je první krok k paralelizaci tohoto algoritmu, protože tyto předvypočítané řešení mohou být následně zpracovány paralelně. Standartně se algoritmus zanořuje do hloubky 8 a predvypočítají se $2^8$ řešení.

2. Paralelní zpracování předvýpočtů: Funkce forSolve zpracovává předvypočtené řešení paralelně. Každé vlákno zpracovává jedno řešení nezávisle na ostatních vláknech. Toto je dosaženo pomocí direktivy #pragma omp parallel for, která rozděluje cyklus mezi dostupná vlákna.

3. Využití kritické sekce: Stejně jako v předchozím algoritmu, i zde je kritická sekce kódu, která aktualizuje globální minimální cenu řezu a ukládá aktuální nejlepší rozdělení uzlů, chráněna pomocí direktivy #pragma omp critical.

4. Dynamické plánování: V tomto algoritmu je použito dynamické plánování (schedule(dynamic)), které umožňuje efektivnější rozdělení práce mezi vlákna, než je tomu u statického plánování.

5. Skladování mezivýsledků pro paralelní zpracování: Paralelní řešení ukládá všechna potenciálních řešení v paměti pro následné paralelní zpracování. To zahrnuje vytvoření a ukládání všech možných rozdělení uzlů grafu do vektoru preComputedSolutions. Každé potenciální řešení je reprezentováno vektorem párů, kde každý pár obsahuje ukazatel na uzel a třídu uzlu (X nebo Y).

Co se týče funkce cutPrice, ta zůstává stejná jako v sekvenčním řešení. Tato funkce počítá cenu řezu pro dané rozdělení uzlů grafu.

Výstup

Výstup algoritmu je stejný jako u sekvenčního algoritmu.

Popis paralelniho algoritmu a jeho implementace v MPI

Algoritmus

Tento paralelní algoritmus je implementován pomocí modelu Message Passing Interface (MPI), který je často používán pro programování paralelních aplikací v distribuovaných systémech. V tomto modelu každý proces spouští stejný program, ale s různými daty. Procesy potom komunikují mezi sebou pomocí zasílání a přijímání zpráv.

Tento konkrétní algoritmus používá strukturu Master-Slave. Master proces je zodpovědný za distribuci úloh mezi Slave procesy, zatímco Slave procesy provádějí dané úlohy a výsledky zasílají zpět Masterovi. Samotný algoritmus je odvozen z OpenMP - task paralelismu s využitím 20 vláken pro každého slave.

Master

1. Master proces nejprve vygeneruje všechny možné řešení pomocí funkce fillPossibleSolutions.
2. Poté rozešle úvodní úlohy mezi Slave procesy.
3. Poté přijímá výsledky od Slave procesů a pokud je ještě nějaká úloha k dispozici, tak ji rozešle Slave procesu, který právě dokončil svou úlohu.
4. Jakmile jsou všechny úlohy rozeslány, Master proces pokračuje v přijímání finálních výsledků od Slave procesů.
5. Nakonec pošle zprávu o ukončení všem Slave procesům.

Slave

1. Slave proces neustále čeká na data od Mastera.
2. Jakmile přijme data, zpracuje je a pošle výsledky zpět Masterovi.
3. Pokud přijme zprávu o ukončení, ukončí svou činnost.

Serializace a deserializace dat

V algoritmu jsou použity čtyři funkce pro serializaci a deserializaci: serializeMap() a deserializeMap(). Tyto funkce umožňují převod datových struktur (map) do formátu, který lze přenést mezi různými procesy v MPI, a zpět.

Map

1. Serializace mapy (serializeMap()): Tato funkce přijímá mapu a vrací ji ve formě std::string. Každý klíč a hodnota v mapě je převeden na řetězec a všechny tyto řetězce jsou spojeny do jednoho dlouhého řetězce. Klíče a hodnoty jsou odděleny specifickým oddělovačem (v tomto případě je to znak mezera)

2. Deserializace mapy (deserializeMap()): Tato funkce přijímá řetězec a vrací ho ve formě mapy. Funkce rozdělí vstupní řetězec na základě oddělovače a převede každý získaný podřetězec zpět na pár klíč-hodnota v mapě.

Výstup

Výstup algoritmu je stejný jako u sekvenčního algoritmu.

Měření výsledků a vyhodnocení

Tento graf, ukazuje průměrný čas řešení (v milisekundách) v závislosti na počtu vláken pro různé algoritmy. Data jsou seskupena podle algoritmu a pro každý algoritmus se vypočítá průměrný čas řešení pro různé počty vláken. Na x-ové ose grafu je zobrazen počet vláken, na y-ové ose je průměrný čas řešení v milisekundách.

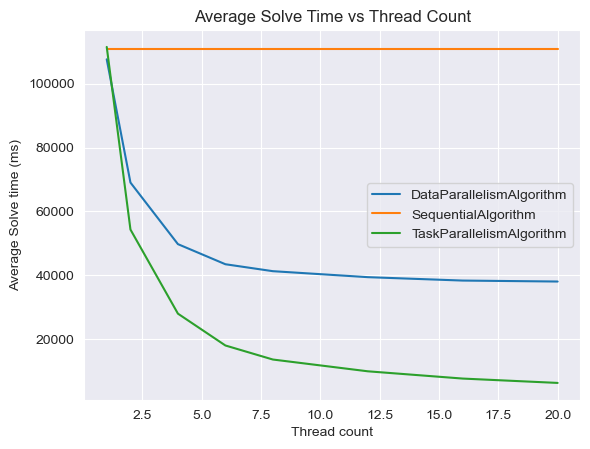
Tento graf, ukazuje průměrné zrychlení (Speed Uplift) v porovnání s baseline hodnotou pro různé algoritmy v závislosti na počtu vláken. Baseline čas je definován jako nejpomalejší čas řešení pro daný počet vláken napříč všemi algoritmy. Speed Uplift, je vypočítán jako poměr baseline času k průměrnému času řešení. Na x-ové ose grafu je zobrazen počet vláken, na y-ové ose je průměrné zrychlení oproti baseline.

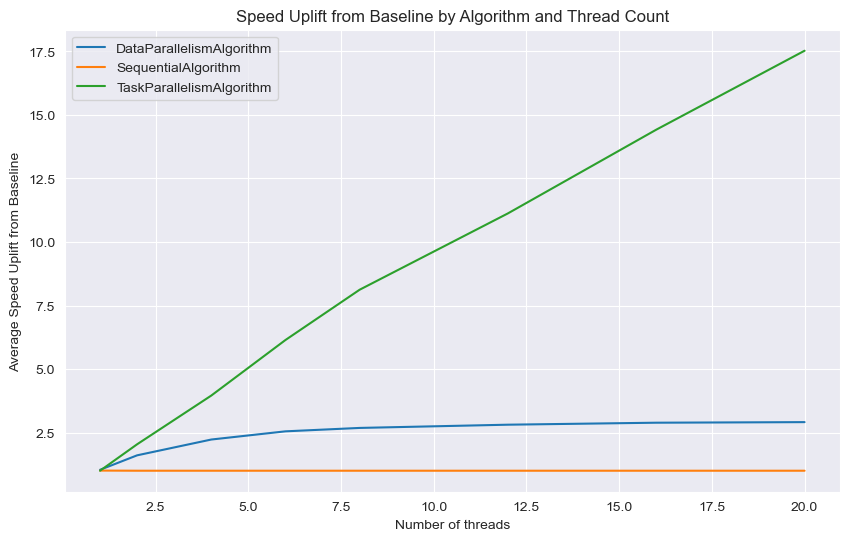
Tento graf, ukazuje průměrný čas řešení (v milisekundách) v závislosti na velikosti světa (World size) pro algoritmus 'MpiParallelismAlgorithm'. Data jsou seskupena podle velikosti světa a pro každou velikost světa je vypočítán průměrný čas řešení. Na x-ové ose grafu je zobrazena velikost světa, na y-ové ose je průměrný čas řešení v milisekundách.

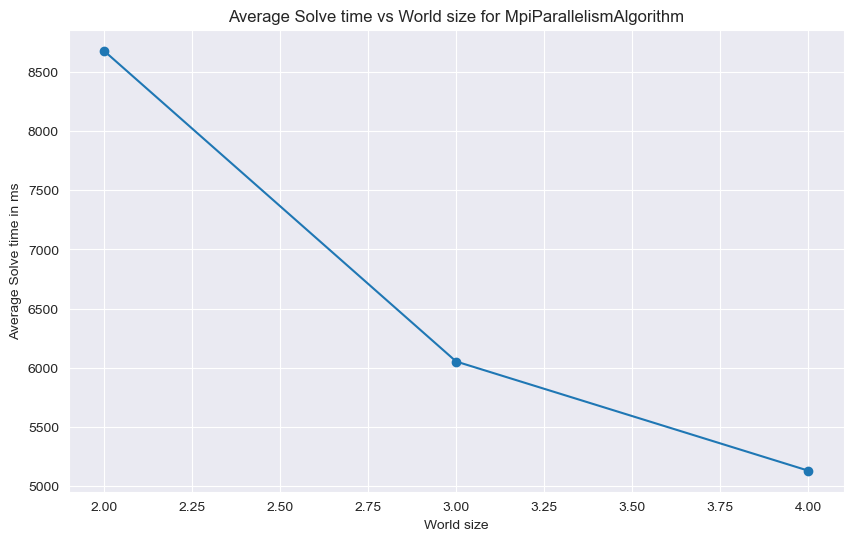
Tato heatmapa ukazuje průměrné zrychlení (Speed Uplift) pro kombinace různých algoritmů, počtů vláken a velikostí světa pro různé grafy (Graph name). Barvy na heatmapě reprezentují hodnoty zrychlení, kde tmavší barvy představují vyšší hodnoty zrychlení. Každá buňka na heatmapě odpovídá konkrétní kombinaci grafu, algoritmu, počtu vláken a velikosti světa.

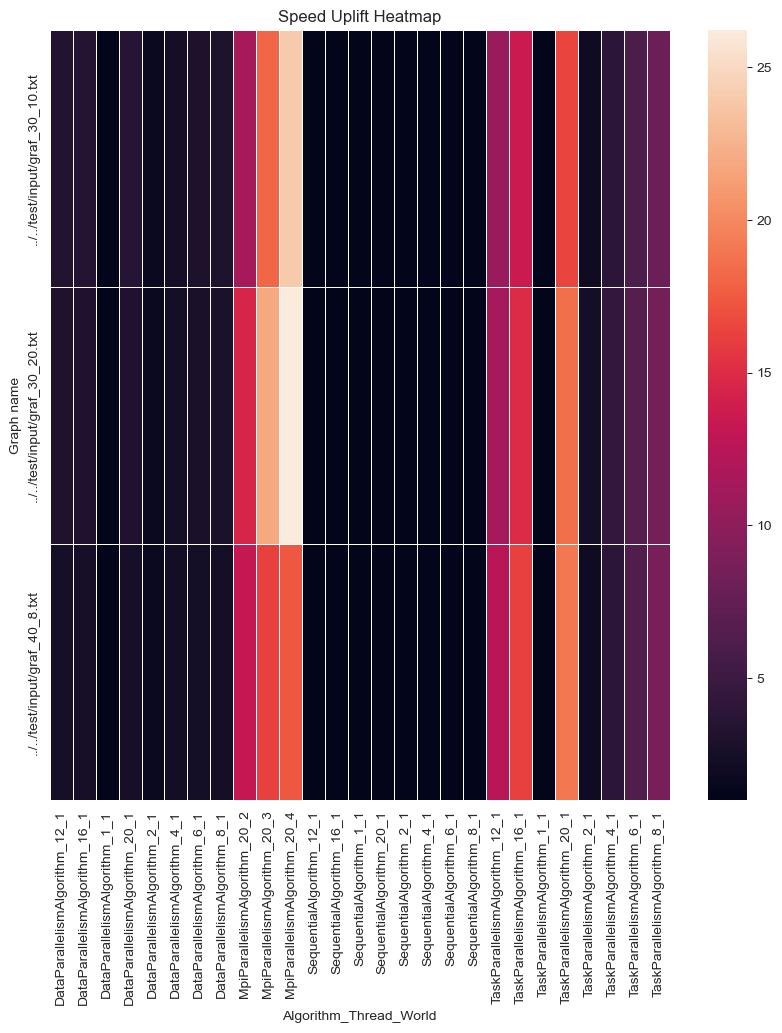
Manuálová stránka pro příkazovou řádku

NAME
    MinHrazRez - program pro výpočet minimálního hranového řezu hranově ohodnoceného grafu.

SYNOPSIS
    MinHrazRez [OPTIONS]

DESCRIPTION
    MinHrazRez je nástroj pro výpočet minimálního hranového řezu hranově ohodnoceného grafu. Program implementuje různé algoritmy pro řešení tohoto problému a umožňuje definovat parametry pro optimalizaci výpočtu.

OPTIONS
    -cut_size_x=<value>
        Určuje velikost skupiny podél osy X při dělení grafu do skupin X a Y. Hodnota by měla být celé číslo.

    -file_location=<path>
        Cesta k souboru obsahujícímu graf, na kterém se má algoritmus spustit.

    -algorithm=<name>
        Název algoritmu, který se má použít pro výpočet minimálního hranového řezu. Možnosti zahrnují "Sequential", "DataParallelism", "TaskParallelism" a "MpiParallelism".

    -threads=<number>
        Počet vláken, které mají být použity pro paralelní algoritmy. Hodnota by měla být celé číslo.

EXAMPLES
    MinHrazRez -cut_size_x=10 -file_location=./data/graph.txt -algorithm=DataParallelism -threads=4
        Spustí algoritmus DataParallelism na grafu definovaném v souboru ./data/graph.txt, s využitím 4 vláken a dělením grafu do skupin o velikosti 10 podél osy X.

EXIT STATUS
    Program vrací 0, pokud je úspěšně dokončen. Jiné hodnoty signalizují chybu.

Závěr

V této práci byly prezentovány různé algoritmy pro výpočet minimálního hranového řezu hranově ohodnoceného grafu. Sekvenční algoritmus využívá techniky prohledávání do hloubky a ořezávání (branch and bound), aby nalezl optimální rozdělení uzlů do dvou skupin s minimální cenou řezu.

Paralelní algoritmus implementovaný s využitím taskového paralelismu v OpenMP a paralelní algoritmus implementovaný v MPI dosahuji výrazného zrychlení ve srovnání se sekvenčním algoritmem. Taskový paralelismus umožňuje efektivně rozdělit výpočet mezi dostupná vlákna, čímž se zkrátí celkový čas výpočtu. V případě paralelního algoritmu implementovaného v MPI je nutné řešit komunikaci mezi procesy, což přináší značnou režii, která omezuje dosažené zrychlení oproti táskovému paralelismu.

Na druhou stranu, datový paralelismus v OpenMP dosahuje pouze jemného zrychlení. To je způsobeno neefektivním využitím vláken.

Výsledky měření naznačují, že taskový paralelismus v OpenMP je vhodnou volbou pro efektivní řešení problému minimálního hranového řezu hranově ohodnoceného grafu. Naopak, datový paralelismus v OpenMP a paralelní algoritmus implementovaný v MPI by měly být použity s opatrností a s ohledem na jejich specifické vlastnosti a požadavky na komunikaci.

Literatura

1. Prednášky z předmětu NI-PDP (Paralelní a distribuované algoritmy) na ČVUT FIT, courses.fit.cvut.cz.

2. Manuálové stránky k OpenMP poskytnuté na webové stránce ČVUT FIT, OpenMP - FIT ČVUT.

3. ChatGPT, AI model vyvinutém společností OpenAI, openai.com

   1. Je důležité poznamenat, že model ChatGPT, vyvinutý společností OpenAI, byl využit jako pomocný nástroj při tvorbě tohoto textu. Dále byl použit pro poskytování informací a návrhy týkající se programování, algoritmů a paralelního zpracování.