Lineární model a základní značení

Uvod¶

Linearni model:

$Y = w_0 + \sum_{i=1}^px_iw_i +\varepsilon$

Zavedeme $X_0=x_0=1$ a vektorove znaceni:

$x=(1,x_1,...,x_p)^T \ \ \ \ \text{ a } \ \ \ \ w=(w_0,w_1,...,w_p)^T$

Muzeme psat:

$Y=w^Tx + \varepsilon$

Ted vezmeme nahodnym vyberem $x_1,...x_n$ muzeme pak psat:

$Y = \begin{pmatrix} Y_1 \\ Y_2 \\ \vdots \\ Y_n \end{pmatrix} \ \ \ \text{a} \ \ \ X= \begin{pmatrix} x_1^T \\ x_2^T \\ \vdots \\ x_n^T \end{pmatrix} = \begin{pmatrix} x_{1;0} & x_{1;1} & x_{1;2} & \dots & x_{1;p} \\ x_{2;0} & x_{2;1} & x_{2;2} & \dots & x_{2;p} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ x_{n;0} & x_{n;1} & x_{n;2} & \dots & x_{n;p} \\ \end{pmatrix}$

A ve forme matice to je:

$Y=Xw+\varepsilon$

Znaceni pro jednotkovou matici $N \times N$ je: $I_N$ Rozptyl se znaci: $\omega^2$

Residuální suma čtverců¶

Definice $RSS(w)= \sum_{i=1}^N(Y_i-\sum_{j=1}^px_{i,j}w_j)^2= ||Y-Xw||^2= (Y-Xw)^T(Y-Xw)$ Hledáme tedy: $\hat{w} = argmin_{w∈Rp+1}\ RSS(w).$ Po zderivovaní a zderivovaní podruhé získáme vztah a hesian, z nich dokážeme ukázat ze Hesian je pozitivně definitní a jakýkoliv kritický bod je globálním minimem RSS. Z toho nam vypadne ze nutnou podminkou minima je platnost vztahu který bývá nazýván normální rovnice: $X^TX\hat{w} = X^TY$ Předpokládejme nyní, že matice je regulární. V takovém případě dostaneme jednoznačné řešení: $\hat{w} = (X^TX)^{−1} X^TY$ Muzeme oznacit matici jako: $P=(X^TX)^{-1}X^T$

Statistické vlastnosti odhadu vektorů vah v lineární regresi¶

Předpokládá se, že data pocházejí z určitého modelu a že máme nějaké předpoklady o chybě $\varepsilon$ , konkrétně že $E \varepsilon = 0$ . Z toho plyne, že očekávaná hodnota Y je $E Y = Xw$ .

Nestranný odhad¶

Věta 1.1 nám říká, že odhad $\hat{w}$ získaný metodou nejmenších čtverců je za předpokladu $E \varepsilon = 0$ nestranný, což znamená, že $E \hat{w} = w$ . To lze dokázat následujícím způsobem:

$E \hat{w} = E ((X^TX)^{-1}X^TY) = (X^TX)^{-1}X^T E Y = (X^TX)^{-1}X^TXw = w$

Variance odhadu ( $σ^2$ )¶

Pokud předpokládáme, že chyby $\varepsilon_i$ v jednotlivých bodech $x_i$ jsou nekorelované veličiny se stejným rozptylem $\sigma^2$ plyne, že $varY = \sigma^2 I_N$

( Vsuvka k důkazu: $var\ (BX)=B\ var(X)\ B^T$ )

Věta 1.2 říká, že za předpokladu $E \varepsilon = 0$ a $var \varepsilon = \sigma^2 I_N$ platí $var \hat{w} = \sigma^2 (X^TX)^{-1}$ . To lze dokázat tak, že použijeme vlastnosti variancí a symetrie matice $(X^TX)$ a její inverze:

$var\ \hat{w} = var\ ((X^TX)^{-1}X^TY) = (X^TX)^{-1}X^T var\ (Y)X (X^TX)^{-1} = (X^TX)^{-1}X^T(\sigma^2 I_N)X (X^TX)^{-1} = \sigma^2 (X^TX)^{-1}X^TX (X^TX)^{-1} = \sigma^2 (X^TX)^{-1}$

Nestrannost odhadu ( $σ^2$ )¶

Věta 1.3 je o tom, že pokud předpokládáme, že chyba $\varepsilon$ je centrálně rozdělena se střední hodnotou $E \varepsilon = 0$ a variance $var \varepsilon = \sigma^2 I$ , pak $s^2 = \frac{RSS(\hat{w})}{(N - p - 1)}$ je nestranný odhad $\sigma^2$

( Vsuvka k důkazu definice stopa matice:

$tr\ (A)=\sum_ia_{i,i}$ )
$tr(AB)=tr(BA)$
$tr(ABC)=tr(CAB)=tr(BAC)$

)

Důkaz:

Začneme s výpočtem střední hodnoty reziduálního součtu čtverců (RSS):
1. $E RSS(\hat{w}) = E Y^T(I_N - P)Y$ .
Přeskupíme termíny pomocí vlastností stopy matice :
1. $E Tr Y^T(I_N - P)Y = Tr (I_N - P) E Y Y^T$ .
Využijeme faktu ze $E Y Y^T = varY+EY(EY)^T$ a použijeme lineární vlastnosti očekávané hodnoty a variance:
1. $Tr (I_N - P) E Y Y^T = Tr (I_N - P)σ^2 I_N$ .
Nakonec spočítáme stopu pomocí vztahu pro jednotkovou matici:
1. $σ^2 Tr (I_N - P) = σ^2 (N - p - 1)$ . odtud plyne, že $E[s^2] = \sigma^2$ , tedy $s^2$ je nestranný odhad $\sigma^2$ .

Gauss-Markov theorem¶

Gauss-Markovova věta: Použitím metody nejmenších čtverců pro odhad vektoru vah $\hat{w}$ získáme "nejlepší" nestranný odhad $w$ v lineárním modelu v $Y$ . Pro jakýkoliv vektor $c$ v $\mathbb{R}^{N}$ , odhad $c^{T} \hat{w}$ bude mít menší nebo rovno variabilitu (rozptyl) než jakýkoli jiný nestranný odhad $d^{T}Y$ , pro jakýkoliv vektor $d$ v $\mathbb{R}^{N}$ . Tedy: $var(c^{T} \hat{w}) \leq var(d^{T}Y)$

Důkaz:

Začínáme s identitou $c^{T} \hat{w} = c^{T}(X^{T}X)^{-1}X^{T}X\hat{w} = c^{T}(X^{T}X)^{-1}X^{T}\hat{w}$
Přejmenováním $a = c^{T}(X^{T}X)^{-1}X^{T}$ , z lemma (1.4) dostáváme, že $a^{T}X\hat{w}$ je nejlepší nestranný lineární v $Y$ odhad $a^{T}Xw = c^{T}(X^{T}X)^{-1}X^{T}Xw = c^{T} w$ .

Testy hypotéz o složkách vektoru vah v lineární regresi, pásy spolehlivosti¶

Testování hypotéz o složkách vektoru vah v lineární regresi¶

Předpokládejme, že máme vektor náhodných odchylek $ε$ s N-rozměrným normálním rozdělením, kde střední hodnota je nulová $E \varepsilon = 0$ a varianční matice je $var\ \varepsilon = \sigma^2I$ . Toto nám dává rozdělení pro vysvětlované proměnné Y jako $Y \sim N(Xw, \sigma^2I_N)$ .

Pod tímto předpokladem, můžeme představit následující věty a důsledky:

Rozdělení Odhadovaných Vah (Věta 1.11)¶

Jestliže $\varepsilon \sim N(0, \sigma^2I)$ , pak $\hat{w} \sim N(w, \sigma^2(X^TX)^{−1})$ . Tento výsledek je způsoben invariancí normálního rozdělení vůči lineárním transformacím. To znamená, že distribuce odhadovaných vah je normální s daným středem a variancí.

Rozdělení Reziduálního Součtu Čtverců (Věta 1.12)¶

Pokud $\varepsilon \sim N(0, \sigma^2I)$ , pak $RSS(\hat{w})/\sigma^2 \sim \chi^2_{N−p−1}$ . Tato věta se používá k popisu rozdělení reziduálního součtu čtverců $RSS(\hat{w})$ a také k odhadu $\sigma^2$ . Rozdělení $\chi^2_{N−p−1}$ je chi-kvadrát rozdělení s $N-p-1$ stupni volnosti.

Testování Hypotéz o Váhách (Věta 1.13)¶

Pod předpokladem, že , pro každé platí, že $T_c = \frac{c^T(\hat{w} − w)}{\sqrt{s^2c^T(X^TX)^{−1}c}} \sim t_{N−p−1}$ kde $s^2 = RSS(wˆ)/(N−p−1)$ . Toto je tzv. t-statistika, kterou používáme k testování hypotéz o vahách v lineárním regresním modelu.

Testování Hypotéz pro Jednotlivé Váhy (Důsledek 1.14)¶

Za předpokladu, že , pro každé platí $T_i = \frac{(\hat{w}_i − w_i)}{\sqrt{s^2v_{ii}}} \sim t_{N−p−1}$ kde $s^2 = RSS(\hat{w})/(N−p−1)$ a $v_{ii}$ je i-tá diagonální složka matice $(X^TX)^−1$ .

Tyto věty nám umožňují testovat hypotézy o hodnotách jednotlivých složek vektoru $w$ , stejně jako hypotézy o liniích složek vektoru $w$ . Můžeme také konstruovat intervaly spolehlivosti pro tyto hodnoty a linie.

Pásy spolehlivosti a predikční interval¶

V lineární regresi často potřebujeme odhadnout, jak přesné jsou naše předpovědi. K tomu můžeme použít pásy spolehlivosti a predikční intervaly.

Výchozí model¶

Začneme s výchozím modelem, ve kterém máme libovolný bod z prostoru příznaků . Vysvětlovaná proměnná v tomto bodě je určena vztahem $Y_0 = x_0^T w + \varepsilon_0,$ kde $E\ \varepsilon_0 = 0$ a $\text{var}\ \varepsilon_0 = \sigma^2$ . To znamená, že hodnota $Y_0$ je dána lineární kombinací příznaků $x_0$ s koeficienty $w$ , plus nějaká náhodná chyba $\varepsilon_0$ .

Odhad hodnoty regresní přímky¶

Hodnotu regresní přímky v bodě $x_0$ označujeme $E Y_0 = x_0^T w$ a odhadujeme ji pomocí $\hat{Y}_0 = x_0^T \hat{w}$ , což je nestranný bodový odhad $E Y_0$ . Z důsledku věty 1.1 totiž platí

$E \hat{Y}_0 = E x_0^T \hat{w} = x_0^T E \hat{w} = x_0^T w = E Y_0.$

Nyní předpokládáme, že $\varepsilon_0 \sim N(0, \sigma^2)$ . Z věty 1.13 plyne, že standardizovaná chyba následují studentovo t-rozdělení s $(N−p−1)$ stupni volnosti

$\frac{x_0^T (\hat{w} - w)}{\sqrt{s^2x_0^T (X^TX)^{-1}x_0}} = \frac{\hat{Y}_0 - E Y_0}{\sqrt{s^2x_0^T (X^TX)^{-1}x_0}} \sim t_{N−p−1}.$

Interval spolehlivosti pro hodnotu regresní přímky¶

V případě, že chyby jsou normálně rozdělené (), můžeme použít větu 1.13 k určení intervalu spolehlivosti pro hodnotu regresní přímky v bodě . Z toho plyne: $1 - \alpha = P \left( -t^{\alpha/2}_{N-p-1} \leq \frac{\hat{Y}_0 - E Y_0}{\sqrt{s^2x_0^T (X^TX)^{-1}x_0}} \leq t^{\alpha/2}_{N-p-1} \right)$ $= P \left( \hat{Y}_0 - t^{\alpha/2}_{N-p-1} \sqrt{s^2x_0^T (X^TX)^{-1}x_0} \leq E Y_0 \leq \hat{Y}_0 + t^{\alpha/2}_{N-p-1} \sqrt{s^2x_0^T (X^TX)^{-1}x_0} \right)$

Z toho následuje interval spolehlivosti:

$\left( \hat{Y}_0 - t^{\alpha/2}_{N-p-1} \sqrt{s^2x_0^T (X^TX)^{-1}x_0}, \hat{Y}_0 + t^{\alpha/2}_{N-p-1} \sqrt{s^2x_0^T (X^TX)^{-1}x_0} \right)$

Toto je tedy (1 - α)% interval spolehlivosti pro hodnotu regresní přímky $E Y_0$ v bodě $x_0$ .

Pás spolehlivosti pro regresní přímku¶

Pokud chceme získat pás spolehlivosti, který platí ve všech bodech současně, tzv. pás spolehlivosti pro regresní přímku, musíme využít sofistikovanějšího přístupu pomocí Scheffého S-metody. Výsledkem je pás spolehlivosti určený v bodě $x_0$ intervalem

$\left( \hat{Y}_0 - \sqrt{(p + 1)F_{\alpha, p+1, N-p-1}s^2x_0^T (X^TX)^{-1}x_0}, \hat{Y}_0 + \sqrt{(p + 1)F_{\alpha, p+1, N-p-1}s^2x_0^T (X^TX)^{-1}x_0} \right)$

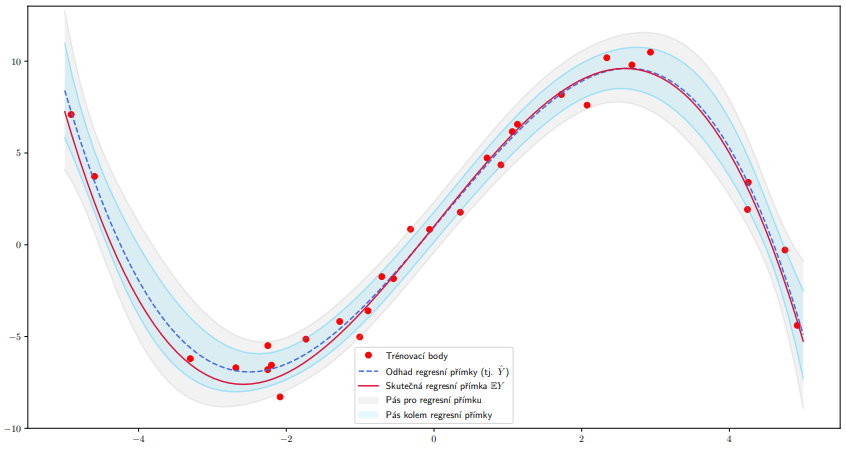
který platí pro všechny body $x_0$ současně. To znamená, že celá regresní přímka je obsažena v pásu určeném tímto intervalem s pravděpodobností 1 - α. Pasted image 20230529231454.png

Odhad hodnoty náhodné veličiny $Y_0$ ¶

Střední hodnotu náhodné veličiny $Y_0$ bodově odhadujeme pomocí $\hat{Y}_0 = x_0^T \hat{w}$ a intervalově pomocí intervalu z předchozí části. Nyní se zabývejme přímo hodnotou náhodné veličiny $Y_0$ .

Číselným odhadem této hodnoty je samozřejmě opět $\hat{Y}_0 = x_0^T \hat{w}$ . Sestrojme nyní interval předpokládaného výskytu, tj. interval, který pokrývá $Y_0$ s předem danou pravděpodobností 1 - α.

Předpokládejme, že v bodě $x_0$ opět platí $Y_0 = x_0^T w + \varepsilon_0$ .

Interval pokrývající $Y_0$ ¶

Pro rozdíl $\hat{Y}_0 - Y_0$ platí $\hat{Y}_0 - Y_0 \sim N \left(0, \sigma^2 (x_0^T (X^TX)^{-1}x_0 + 1)\right)$ . Analogickým postupem jako v důkazu věty 1.13 dostáváme

$\frac{\hat{Y}_0 - Y_0}{\sqrt{s^2 (x_0^T (X^TX)^{-1}x_0 + 1)}} \sim t_{N−p−1}.$

Nyní již stejným postupem jako u intervalu spolehlivosti pro $E Y_0$ zjistíme, že interval pokrývající $Y_0$ s pravděpodobností $1 - α$ je

$\left( \hat{Y}_0 - t_{\frac{\alpha}{2}, N-p-1}\sqrt{s^2 (x_0^T (X^TX)^{-1}x_0 + 1)}, \hat{Y}_0 + t_{\frac{\alpha}{2}, N-p-1}\sqrt{s^2 (x_0^T (X^TX)^{-1}x_0 + 1)} \right)$