Optimalizace

Totální derivace, spádový směr a myšlenka spádových metod

Definice: Mějme funkci $f : D → R$, kde $D ⊂ Rⁿ$ je otevřená množina. Řekneme, že $f$ je (totálně) diferencovatelná v bodě $a \in D$, pokud existuje lineární zobrazení $λ : Rⁿ → Rᵐ$ takové, že

$$\lim_{h \to 0} \frac{\|f(a + h) - f(a) - \lambda(h)\|}{\|h\|} = 0.$$

Pokud je $f$ diferencovatelná v $a \in D$, pak takové lineární zobrazení existuje právě jedno: nazývá se (totální) derivací funkce $f$ v bodě $a \in D$ a značí se $Df(a)$ nebo $f'(a)$.

Jacobiho matice

Matice lineárního zobrazení $Df(a)$ se nazývá Jacobiho matice.

Věta 2.2: Mějme funkci $f : D \rightarrow \mathbb{R}^m$, kde $D \subset \mathbb{R}^n$ je otevřená množina. Je-li $f$ diferencovatelná v bodě $a \in D$, potom $\frac{\partial f_i}{\partial x_j}(a)$ existuje pro všechna $i$ a $j$ taková, že $1 \leq i \leq m$, $1 \leq j \leq n$, a $(Df(a))_{i,j} = \frac{\partial f_i}{\partial x_j}(a)$.

Speciálně pro $m = 1$ dostaneme $Df(a) = \nabla f(a)^T$.

Věta 2.3: Mějme funkci $f : D \rightarrow \mathbb{R}^m$, kde $D \subset \mathbb{R}^n$ a $a \in D$. Pokud $\frac{\partial f_i}{\partial x_j}(a)$ existuje a je spojitá na otevřeném okolí bodu $a$ pro všechna $i$ a $j$ taková, že $1 \leq i \leq m$, $1 \leq j \leq n$, potom $Df(a)$ existuje.

Řetězové pravidlo

Věta 2.4 - Chain Rule: Mějme funkci $g : D_g \rightarrow \mathbb{R}^m$, kde $D_g \subset \mathbb{R}^n$, a $f : D_f \rightarrow \mathbb{R}^q$, kde $D_f \subset \mathbb{R}^m$. Je-li funkce $g$ diferencovatelná v $a \in D_g$ a funkce $f$ diferencovatelná v $g(a) \in D_f$, potom je funkce $f \circ g : D_g \rightarrow \mathbb{R}^q$ diferencovatelná v $a$ a platí

$$D(f \circ g)(a) = Df(g(a)) \cdot Dg(a).$$

Speciálně pro $n = q = 1$ dostaneme

$$D(f \circ g)(a) = Df(g(a)) \cdot Dg(a) = \nabla f(g(a))^T \cdot \begin{pmatrix} \frac{\partial g_1(a)}{\partial a} \\ \vdots \\ \frac{\partial g_m(a)}{\partial a} \end{pmatrix}.$$

Gradient jakožto směr největšího růstu

Gradient funkce $f$, označovaný jako $\nabla f(a)$, je vektor, který obsahuje všechny parciální derivace funkce v bodě $a$. Gradient ukazuje směr, ve kterém funkce roste nejrychleji.

Na derivaci ve směru $s$ funkce $f : D_f \rightarrow \mathbb{R}$ v bodě $a \in D_f \subset \mathbb{R}^n$ můžeme nahlížet jako na derivaci jednorozměrné funkce $h(t) = f(a + ts)$ v bodě 0.

Označme $g(t) = a + ts$. Potom platí

$$Dh(t) = D(f \circ g)(t) = \nabla f(g(t))^T \cdot \begin{pmatrix} \frac{\partial g_1(t)}{\partial t} \\ \vdots \\ \frac{\partial g_m(t)}{\partial t} \end{pmatrix} = \nabla f(a + ts)^T \cdot \begin{pmatrix} s_1 \\ \vdots \\ s_n \end{pmatrix}.$$

Tedy pro bod 0 máme

$$\nabla_s f(a) = Dh(0) = \nabla f(a)^T \cdot s.$$

To nám dává směr největšího růstu funkce v bodě $a$.

Taylorův rozvoj

Taylorův rozvoj nám umožňuje aproximovat funkci pomocí polynomu v okolí daného bodu. Pro funkci $f: \mathbb{R}^n \rightarrow \mathbb{R}$, která je dvakrát diferencovatelná v bodě $a$, můžeme napsat:

$$f(a + \alpha s) = f(a) + \alpha \nabla f(a)^T s + \frac{1}{2} \alpha^2 s^T \nabla^2 f(a) s + o(\alpha^2 \|s\|^2),$$

kde $\nabla^2 f(a)$ je Hessian matice (matice druhých parciálních derivací) a $o(\alpha^2 \|s\|^2)$ je reziduální člen, který konverguje k nule rychleji než $\alpha^2 \|s\|^2$.

Spádové metody

Line Search

Line search je metoda, kde v každém kroku vybereme směr, kterým se chceme posunout (typicky směrem opačným k gradientu), a pak hledáme optimální délku kroku v tomto směru. Tedy v každé iteraci hledáme novou pozici podle vzorce

$$x_{k+1} = x_k + \alpha_k p_k,$$

kde $x_k$ je současná pozice, $p_k$ je směr kroku, a $\alpha_k$ je délka kroku, kterou nalezneme řešením problému

$$\alpha_k = \text{argmin}_{\alpha \geq 0} f(x_k + \alpha p_k).$$

Tedy hledáme takovou délku kroku, která minimalizuje hodnotu funkce v nové pozici.

Trust Region

Trust region přístup je trochu odlišný. Místo hledání optimální délky kroku v daném směru, hledáme přímo novou pozici v okolí současné pozice. Toto okolí, kterému věříme (odtud název "trust region"), je omezeno koulí o poloměru $\Delta_k$.

V každém kroku tedy hledáme novou pozici podle vzorce

$$x_{k+1} = x_k + p_k,$$

kde $x_k$ je současná pozice a $p_k$ je vektor posunu, který nalezneme řešením problému

$$p_k = \text{argmin}_p \{m_k(x_k + p) \, | \, \|p\| \leq \Delta_k\},$$

kde $m_k$ je nějaká aproximace funkce $f$ v okolí bodu $x_k$. Tedy hledáme takový posun, který minimalizuje hodnotu aproximace funkce v nové pozici, za podmínky, že jsme stále v okolí, kterému věříme.

Volba délky kroku ve spádových metodách

Spádový směr

Pro výpočet následující aproximace $x_{k+1}$ používáme vzorec:

$$x_{k+1} = x_k + \alpha_k p_k,$$

kde $p_k$ je zvolený směr a $\alpha_k$ je délka kroku.

Obecná volba směru: směr spádu (descent): $\nabla f(x_k)^T \cdot p_k < 0$.

Častá volba je $p_k = -B_k^{-1} \nabla f(x_k)$, kde:

• $B_k = I$ - metoda největšího spádu (steepest descent),
• $B_k = \nabla^2 f(x_k)$ - Newtonova metoda,
• $B_k \approx \nabla^2 f(x_k)$ - kvazi-Newtonova metoda.

Pokud je $B_k$ pozitivně definitní, pak se jedná o spádový směr.

Volba délky kroku

Ideální volba $\alpha_k$ do $x_{k+1} = x_k + \alpha_k p_k$ se zdá být minimum funkce

$$\phi(\alpha) = f(x_k + \alpha p_k) \quad \text{pro} \quad \alpha \geq 0.$$

To může být výpočetně složité, a proto se volí i jiný přístup: hledá se nějaká vhodná délka kroku, která zajistí dostatečný pokles funkční hodnoty funkce $f$.

První varianta se nazývá exact line search, kde se přesně hledá optimální $\alpha_k$ pro minimalizaci funkce $\phi(\alpha)$. To může být náročné, protože vyžaduje výpočet funkce $f$ pro různé hodnoty $\alpha$.

Druhá varianta se nazývá inexact line search, kde se hledá pouze vhodná délka kroku, která zajistí dostatečný pokles funkční hodnoty $f$. Často se využívají heuristiky nebo aproximace, které nevyžadují přesnou optimalizaci $\alpha_k$.

Armijova podmínka

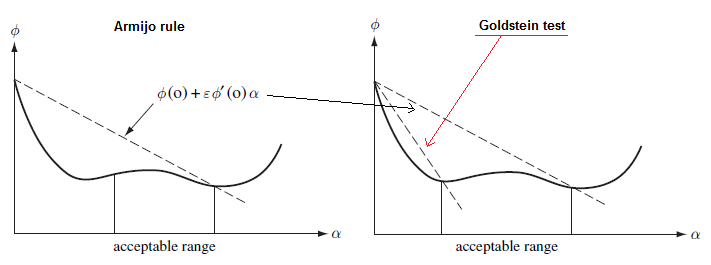
$\phi(\alpha_k) \leq \phi(0) + \alpha_k c \phi'(0)$, kde $c$ je zvolené číslo tak, aby $0 < c < 1$. Tato podmínka zajišťuje, že funkční hodnota leží pod zvolenou přímkou a zároveň se zabrání příliš malému kroku.

Goldsteinova podmínka

$\phi(0) + \alpha_k (1 - c) \phi'(0) \leq \phi(\alpha_k) \leq \phi(0) + \alpha_k c \phi'(0)$, kde $c$ je zvolené číslo tak, aby $0 < c < \frac{1}{2}$. Tato podmínka zajišťuje, že funkční hodnota leží mezi zvolenými přímkami, čímž se omezí nevhodné příliš malé kroky. Může vést k tomu, že se přehlédne optimální hodnota pro $\alpha_k$.

Wolfeho (slabá) podmínka

1. $\phi(\alpha_k) \leq \phi(0) + \alpha_k c_1 \phi'(0)$,
2. $\phi'(\alpha_k) \geq c_2 \phi'(0)$,

Kde $c_1$ a $c_2$ jsou zvolené čísla tak, aby $0 < c_1 < c_2 < 1$. Tato podmínka kombinuje omezení funkční hodnoty s omezením derivace $\phi'(\alpha_k)$. Tedy prvni podminka zase rika ze hodnota ma byt pod primkou a fruha podminka rika ze sklon neboli prvni derivace ma byt vyzsi nez puvodni zklon, Sklon je vyzsi pokud je vice vodorovny nebo skloneni na opacnou stranu tedy pokud je sklon: $\searrow$ tak vetsi je nepriklad: $\longrightarrow$ nebo: $\nearrow$.

Wolfeho silná podmínka

1. $\phi(\alpha_k) \leq \phi(0) + \alpha_k c_1 \phi'(0)$,
2. $|\phi'(\alpha_k)| \leq c_2 |\phi'(0)|$

Kde $c_1$ a $c_2$ jsou zvolené čísla tak, aby $0 < c_1 < c_2 < 1$. Tato podmínka přidává absolutní hodnotu k omezení derivace $\phi'(\alpha_k)$, aby se zajistilo, že derivace nemá příliš velké hodnoty. Tedy prvni podminka zase rika ze hodnota ma byt pod primkou a druha podminka rika ze sklon neboli prvni derivace ma byt absolutne vyzsi nez puvodni zklon, Sklon je absolutne vyzsi pokud je vice vodorovny tedy pokud je sklon: $\searrow$ tak vetsi je nepriklad: $\longrightarrow$.

Nevázaná/volná optimalizace: metoda největšího spádu, Newtonova metoda a stochastický gradientní sestup

Metoda největšího spádu

Metoda největšího spádu, je iterativní optimalizační algoritmus používaný pro nalezení lokálního minima funkce. Využívá se zejména při hledání řešení problémů s velkým počtem proměnných, kde jsou ostatní techniky neefektivní.

Metoda největšího spádu pracuje tak, že v každém bodě prostoru vypočítá gradient funkce (více-dimenzionálný analog derivace) a poté se posune o krok v opačném směru k gradientu. Toto je směr, ve kterém funkce klesá nejrychleji. Pokud definujeme směr kroku $p_k = -\nabla f(x_k)$, kde $\nabla f(x_k)$ je gradient funkce v bodě $x_k$, můžeme iterativně vypočítat další kroky jako:

$$x_{k+1} = x_k + \alpha_k p_k,$$

kde $\alpha_k$ je délka kroku, která se volí tak, aby minimalizovala hodnotu funkce v novém bodě $x_{k+1}$. Volba délky kroku může být řízena různými podmínkami, jako je například Armijova podmínka.

Newtonova metoda

Základní Princip

Pokud máme funkci $f$ a aktuální přiblížení k řešení $x_k$, další přiblížení $x_{k+1}$ se počítá následujícím způsobem:

$$x_{k+1} = x_k - \alpha_k p_k,$$

kde $\alpha_k$ je délka kroku a $p_k$ je směr kroku, který je v Newtonově metodě daný jako

$$p_k = - [\nabla^2f(x_k)]^{-1} \nabla f(x_k).$$

Zde $\nabla^2f(x_k)$ je Hessian funkce $f$ v bodě $x_k$ a $\nabla f(x_k)$ je gradient funkce $f$ v bodě $x_k$.

Konvergence

Pokud je počáteční přiblížení $x_0$ dostatečně blízko minima $x*$, pak Newtonova metoda konverguje kvadraticky k $x*$. To znamená, že existuje konstanta $L$ taková, že

$$\lim_{k\to\infty} \frac{||x_{k+1} - x*||}{||x_k - x*||^2} < L.$$

Toto platí jen pokud jsme již blízko minima. Pokud je počáteční bod daleko od minima, nebo funkce $f$ má více lokálních minim, Newtonova metoda může konvergovat k nějakému jinému bodu.

Metoda konverguje k optimálnímu bodu kvadraticky rychle pokud:

1. Funkce, kterou optimalizujeme, je dvakrát spojitě diferencovatelná.

2. Gradient této funkce je v bodě minima nulový a její Hessian (druhé derivace) je v tomto bodě "pozitivně definitní", tj. má pouze kladné vlastní hodnoty.

3. Hessian je "Lipschitzovsky spojitý" v okolí tohoto minima. To znamená, že se nemění příliš rychle.

4. $x_0$ je dostatečně blízko minima $x*$

Pokud jsou splněny tyto podmínky, Newtonova metoda konverguje kvadraticky rychle, což znamená, že počet přesných číslic v aproximaci se zdvojnásobí s každým krokem. Toto platí pro počáteční bod dostatečně blízký k minimu.

Dále, výpočty gradientu konvergují také kvadraticky rychle k nule.

Pozitivní definitnost Hessianu

Matice $∇^2f(xk)$ nemusí být pozitivně definitní, a tedy její inverze nemusí existovat. V takový okamžik ji lze modifikovat, aby inverze existovala: přesněji abychom mohli vyřešit $B_kp_k = −∇f(x_k)$

Kvazinewtonovské metody

Kvazinewtonovské metody nějakým způsobem aproximují matici $∇^2f(xk)$ a snaží se tak vylepšit celkově algoritmus, například tím, že matice $B_{k+1}$ se napočítává aktualizací matice $B_k$. Obecný postup pro nastavení matice $B_k = \nabla^2 f(x_k) + E_k$ tak, aby $B_k$ byla pozitivně definitní, zahrnuje několik možností: - změnou záporných vl. čísel - přičtení kladné diagonální matice - modifikace nějakého rozkladu matice $∇^2f(xk)$

Stochastický gradientní sestup

Stochastický gradientní sestup je varianta metody gradientního sestupu, která aktualizuje parametry modelu pomocí gradientu pouze jedné vzorkové instance místo celého datasetu. Toto může významně zrychlit trénování na velkých datasetech.

Základní princip

V každé iteraci, SGD vybere náhodně jednu instanci $(x_i, y_i)$ z trénovací sady a vypočte gradient na této instanci. Matematicky, to znamená:

$$w_{k+1} = w_k - \alpha_k \nabla Q_i(w_k),$$

kde $w_k$ je vektor parametrů modelu v kroku $k$, $\alpha_k$ je délka kroku a $\nabla Q_i(w_k)$ je gradient funkce ztráty $Q_i$ na instanci $(x_i, y_i)$.

Volba kroku

Stejně jako u metody největšího spádu, délka kroku $\alpha_k$ může výrazně ovlivnit rychlost konvergence metody. Obecně se používá strategie, kdy délka kroku klesá s počtem iterací, například $\alpha_k = 1/(\lambda k)$, kde $\lambda$ je konstanta.

Konvexní funkce: definice a vlastnosti vzhledem k optimalizační úloze

Konvexita

1. Konvexní množina $\Omega \subset \mathbb{R}^n$ je taková, že $\alpha x + (1 - \alpha)y \in \Omega$ pro všechna $x, y \in \Omega$, a všechna $\alpha \in [0, 1]$. Tedy s každými dvěma body $x,y$ leží v množině všechny body na úsečce mezi nimi.

2. Konvexní funkce $f : \Omega \rightarrow \mathbb{R}$ je taková, že pro všechna $x, y \in \Omega$ a $\alpha \in [0, 1]$ platí $f(\alpha x + (1 - \alpha)y) \leq \alpha f(x) + (1 - \alpha)f(y)$.

3. Ryze konvexní funkce má navíc podmínku, že pro všechna $x, y \in \Omega$, $x \neq y$, a všechna $\alpha \in (0, 1)$ platí $f(\alpha x + (1 - \alpha)y) < \alpha f(x) + (1 - \alpha)f(y)$.

Operace s konvexními množinami a funkcemi

1. Pro konvexní $f : \Omega \rightarrow \mathbb{R}$ platí, že $\{x \in \Omega | f(x) \leq c\}$ (sublevel set) je konvexní.

2. Průnik konečně či nekonečně mnoha konvexních množin je konvexní množina.

3. Afinní zobrazení konvexní množiny je konvexní množina.

4. Afinní transformace proměnných zachová konvexitu funkce.

5. Je-li $f$ konvexní a $g$ konvexní a monotónní funkce, pak $g \circ f$ je konvexní.

Konvexní funkce - podmínky 1. řádu

První řádové podmínky jsou důležité, protože nám poskytují jednoduchou metodu, jak ověřit, zda je funkce konvexní, pokud je spojitě diferencovatelná.

1. Pokud je $f$ spojitě diferencovatelná a $\Omega$ je konvexní, $f$ je konvexní právě tehdy, když pro všechna $x, y \in \Omega$, platí: $$f(y) \geq f(x) + \nabla f(x)^T(y - x)$$

2. Podobně, $f$ je ryze konvexní právě tehdy, když pro všechna $x, y \in \Omega$, $x \neq y$, platí $$f(y) > f(x) + \nabla f(x)^T(y - x)$$

3. Mějme problém konvexní optimalizace, tj. minimalizace funkce $f(x)$ pro $x \in \Omega$, kde $\Omega \subset \mathbb{R}^n$ je konvexní množina a $f : \Omega \rightarrow \mathbb{R}$ je konvexní funkce. Je-li funkce $f$ spojitě diferencovatelná, potom je bod $x^* \in \Omega$ bodem globálního minima právě tehdy, když $$\forall y \in \Omega, \nabla f(x^*)^T (y - x^*) \geq 0$$ Což v podstatě znamená, že pokud se pohneme od bodu $x^*$ do jakéhokoliv jiného bodu $y$ v množině $\Omega$, hodnota funkce $f$ nebude klesat.

Konvexní funkce - podmínka 2. řádu

Druhá řádová podmínka je rovněž důležitá pro ověřování konvexity funkcí, které jsou dvakrát diferencovatelné. Tato podmínka říká, že funkce je konvexní, pokud je její Hessiánská matice (matice druhých derivací) pozitivně semidefinitní v každém bodě.

Znaceni konvexity: - $B ⪰ 0$: $B$ je pozitivně semidefintní; - $B ≻ 0$: $B$ je pozitivně definitní

Pokud je $f$ dvakrát spojitě diferencovatelná a $\Omega$ je konvexní a otevřená, $f$ je konvexní právě tehdy, když pro všechna $x \in \Omega$, platí $\nabla^2 f(x) \succeq 0$. Neboli funkce je konvexní právě tehdy, když je konvexní její Taylorova aproximace (v každém bodě).

Konvexita v metodě největšího spádu

Pokud má konvexní funkce spojitý Lipschitzovský gradient, lze odhadnout rychlost konvergence metody gradientního sestupu. Pro velikost kroku maximálně $1/L$, kde $L$ je Lipschitzova konstanta gradientu, lze omezení odchylky funkční hodnoty od minimální hodnoty vyjádřit kvadratickou funkcí vzdálenosti počátečního bodu od minima.

Pokud je $f$ konvexní, $\nabla f$ L-Lipschitzovsky spojitá (v Eukl. normě), a existuje-li bod minima $x^*$, potom pro $\alpha_k = \alpha \leq 1/L$ platí $$f(x_k) - f(x^*) \leq \frac{||x_0 - x^*||^2}{2\alpha_k}$$

Pro konvexní kvadratickou funkci metoda největšího spádu konverguje exponenciálně rychle. Rychlost konvergence je dána největším a nejmenším vlastním číslem Hessiánské matice funkce.