SVM Regrese

SVM regrese - prvotní formulace pomocí vázaných extrémů¶

Úvod¶

Support Vector Machines (SVM) regrese je metoda založená na principu SVM, která je primárně určena pro klasifikaci. V kontextu regrese se SVM používá k modelování vztahu mezi závislou a nezávislou proměnnou.

Definice¶

Základní model vztahu mezi závislou proměnnou $Y$ a nezávislým vektorem příznaků $X$ lze vyjádřit jako:

$Y = \sum_{j=1}^{M} w_j \phi_j (X) + w_0 + \varepsilon = \phi(X)^T w + w_0 + \varepsilon$

kde $X = (X_1, \ldots, X_p)^T$ je náhodný vektor příznaků, $\phi = (\phi_1, \ldots, \phi_M)^T$ je vektor bázových funkcí, $w = (w_1, \ldots, w_M)^T$ je vektor neznámých koeficientů, $w_0$ je neznámý koeficient zvaný intercept a $\varepsilon$ je náhodná veličina s $E\varepsilon = 0$ .

Bázové funkce $\phi_j$ , $j=1,\ldots,M$ umožňují představit lineární vztah v transformovaném prostoru příznaků, který může být nelineární v původním prostoru příznaků. Můžeme použít různé typy bázových funkcí, včetně polynomiálních, gaussovských a dalších.

ε necitlivá ztrátová funkce¶

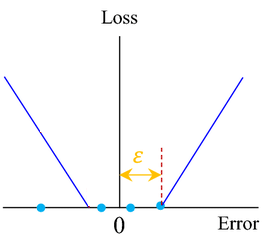
V rámci SVM regrese se používá specifická ztrátová funkce $L_{\varepsilon}$ , známá jako $\varepsilon$ -necitlivá ztrátová funkce, definovaná následovně:

$L_{\varepsilon}(Y, \hat{Y}) = \max\{ |Y - \hat{Y}| - \varepsilon, 0 \}$

Tato funkce nabízí robustní odhad chyby pro hodnoty v rozmezí $\varepsilon$ , kde $|Y - \hat{Y}| \leq \varepsilon$ .

Minimalizovana funkce¶

Cílem je minimalizovat funkci $J$ , která je definována následovně:

$J = C \sum_{i=1}^{N} L(Y_i, \hat{Y_i}) + \frac{1}{2} ||w||^2$

kde $C = 1/(2\lambda)$ je konstanta a $L$ je $\varepsilon$ -necitlivá ztrátová funkce.

Reformulace pomocí vázaného extrému¶

Vzhledem k výběru ztrátové funkce je proces minimalizace komplikovaný, protože $J_{\varepsilon}$ není všude diferencovatelná podle složek $w$ . Proto se problém řeší pomocí reformulace do problému vázaného extrému.

Volné (slack) proměnné¶

Pro každý bod trénovací množiny se definují dvě volné proměnné $\xi_i^+$ a $\xi_i^-$ , které mají tyto vlastnosti:

Obe dvě jsou nezáporné: $\xi_i^+ \ge 0 \ \ \ \ \xi_i^- \ge 0$ ,
$\xi_i^+ \ge Y_i − \hat{Y}_i − \varepsilon$ ,
$\xi_i^- \ge \hat{Y}_i - Y_i − \varepsilon$ .

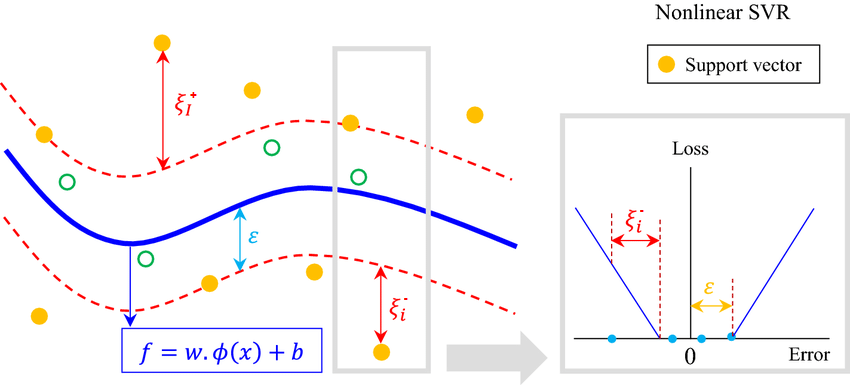
Z čehož plyne: $L_\varepsilon(Y_i, \hat{Y}_i) \leq \xi^{+}_i + \xi^{-}_i$

Nová minimalizující funkce¶

Využitím volných proměnných $\xi_i^+$ a $\xi_i^-$ můžeme reformulovat funkci $J$ takto:

$\tilde{J}_\varepsilon(w_0, w, ξ^+ , ξ^− ) = C \sum_{i=1}^{N} (\xi_i^+ + \xi_i^-) + \frac{1}{2} ||w||^2$

Tímto je problém přeformulován na konvexní optimalizační úlohu, kterou lze efektivně řešit pomocí dostupných optimalizačních algoritmů.

SVM regrese - duální přístup a vlastnosti řešení¶

Duální formulace¶

Minimalizace tohoto vázaného extrému se nejčastěji řeší duální reformulací. Vytváříme odpovídající Lagrangeovu funkci $L$ závislou na proměnných a také na Lagrangeových multiplikátorech.

Definice: Lagrangeova funkce¶

Označme nove multiplikátory:

$\mu^+_i \ \ \Rightarrow \ \ \xi_i^+ \ge 0$
$\mu^-_i \ \ \Rightarrow \ \ \xi_i^- \ge 0$
$\alpha^+_i \ \ \Rightarrow \ \ \xi_i^+ \ge Y_i − \hat{Y}_i − \varepsilon$
$\alpha^-_i \ \ \Rightarrow \ \ \xi_i^- \ge \hat{Y}_i - Y_i − \varepsilon$

Potom definujeme Lagrangeovu funkci $L$ jako:

$\begin{align*} L (w_0, w, \xi^+, \xi^-, \alpha^+, \alpha^-, \mu^+, \mu^-) = \\C \sum_{i=1}^{N} (\xi_i^+ + \xi_i^-) + \frac{1}{2} \|w\|^2 \\- \sum_{i=1}^{N} \alpha_i^+ \left(\xi_i^+ - Y_i + \hat{Y_i} + \varepsilon\right) \\ -\sum_{i=1}^{N} \alpha_i^- \left(\xi_i^- + Y_i - \hat{Y_i} + \varepsilon\right) \\ - \sum_{i=1}^{N} \left(\mu_i^+ \xi_i^+ + \mu_i^- \xi_i^-\right) \end{align*}$

Pro bod ve kterém se nachází minimum platí: - Gradient je rovny nule: $\nabla_{\hat{w}_0,\hat{w},\hat{\xi}_+,\hat{\xi}_-} L = 0$ Lze snadno ukázat, že v našem případě jsou splněny Slaterovy podmínky a platí tedy silná duálnost. Z toho plyne, že primární a duální problém mají stejné optimální hodnoty a že jsou splněny KKT podmínky to znamená ze: $min\ \tilde{J}_\varepsilon(w_0, w, ξ^+ , ξ^− ) = min\ L (w_0, w, \xi^+, \xi^-, \alpha^+, \alpha^-, \mu^+, \mu^-) = max\ \tilde{L}(\alpha^+, \alpha^-, \mu^+, \mu^-)$

Duální problém¶

Duální problém je maximalizace Lagrangeovy funkce $L$ při splnění podmínek $\mu_i^+ \geq 0, \ \ \mu_i^- \geq 0$ a $\alpha_i^+ \geq 0,\ \ \alpha_i^- \geq 0$ . Z rovnice $\nabla_{\hat{w}_0,\hat{w},\hat{\xi}_+,\hat{\xi}_-} L = 0$ dostáváme pro ideální hodnoty $w_0$ , $w$ , $\xi_+$ , a $\xi_-$ následující rovnice (neboli postupně parciálně zderivujeme podle $w_0$ , $w$ , $\xi_+$ , a $\xi_-$ ):

$\begin{align*} 0 &= \sum_{i=1}^{N} (\alpha_i^+ - \alpha_i^-) \\ w_j &= \sum_{i=1}^{N} (\alpha_i^+ - \alpha_i^-) x_i \\ \mu_i^+ &= C - \alpha_i^+ \\ \mu_i^- &= C - \alpha_i^- \\ \end{align*}$

Dosazením rovnic do Lagrangeovy funkce $L$ dostáváme duální problém jako:

$\tilde{L}(\alpha^+_i,\alpha^-_i)= -\frac{1}{2} \sum_{i=1}^{N} \sum_{k=1}^{N} (\alpha_i^+ - \alpha_i^-)K(x_i, x_k)(\alpha_k^+ - \alpha_k^-) - \varepsilon \sum_{i=1}^{N} (\alpha_i^+ + \alpha_i^-) + \sum_{i=1}^{N}(\alpha_i^+ - \alpha_i^-) Y_i$

Který je potřeba maximalizovat. Při splnění podmínek:

$\begin{align*} \sum_{i=1}^{N} (\alpha_i^+ - \alpha_i^-) &= 0 \\ 0 \leq \alpha_i^+, \alpha_i^- &\leq C \\ \end{align*}$

Vlastnosti řešení¶

Představení řešení¶

Řešení SVM regresní úlohy není možné nalézt explicitně. Jedná se ale o standardní úlohu kvadratického programování, která je numericky dobře řešitelná. Označíme-li řešení této úlohy jako $\hat{\alpha_i}^+$ a $\hat{\alpha_i}^-$ , platí tedy:

$\hat{\alpha_i}^+, \hat{\alpha_i}^- = \text{argmax}_{0 \le \alpha^+_i, \alpha^-_i \le C, \sum_{i=1}^N(\alpha^+_i - \alpha^-_i) = 0} L(\hat{\alpha_i}^+, \hat{\alpha_i}^-)$

Vyjádření $w$ ¶

Máme-li $\hat{\alpha_i}^+$ a $\hat{\alpha_i}^-$ můžeme vyjádřit $\hat{w}$ pomocí vztahu:

$\hat{w}_j = \sum_{i=1}^{N} (\hat{\alpha}^+_i - \hat{\alpha}^-_i) \phi_j(x_i)$

Predikce¶

Pro predikci $\hat{Y}_0$ hodnoty $Y_0$ v bodě $x_0$ tak platí:

$\hat{Y}_0 = \hat{w}_0 + \sum_{j=1}^{M} \hat{w}_j \phi_j(x_0) = \hat{w}_0 + \sum_{j=1}^{M} \sum_{i=1}^{N} (\hat{\alpha}^+_i - \hat{\alpha}^-_i) \phi_j(x_i) \phi_j(x_0)$

Spolu s definicí jádrové funkce tak dostáváme finální vyjádření v termínech $\hat{\alpha_i}^+$ , $\hat{\alpha_i}^-$ a $\hat{w}_0$ :

$\hat{Y}_0 = \hat{w}_0 + \sum_{i=1}^{N} (\hat{\alpha}^+_i - \hat{\alpha}^-_i) K(x_0, x_i)$

což tvoří analogii k jádrovému modelu, kde $\alpha_i = (\alpha^+_i + \alpha^-_i)$ .

Možné hodnoty $\hat{\alpha_i}^+$ a $\hat{\alpha}^-$ ¶

Podle KKT podmínek jsou možné následující hodnoty:

$\hat{\alpha}^+_i = \hat{\alpha}^-_i = 0$ : Tento případ odpovídá situaci, kdy bod $x_i$ leží uvnitř $\varepsilon$ pásmu. To znamená, že se bod $Y_i$ nachází mezi $\hat{Y}_i - \varepsilon$ a $\hat{Y}_i + \varepsilon$ .
$0 < \hat{\alpha}^+_i < C$ a $\hat{\alpha}^-_i = 0$ : Tento případ odpovídá situaci, kdy bod $x_i$ leží nad horním okrajem $\varepsilon$ pásmu, tj. $Y_i > \hat{Y}_i + \varepsilon$ .
$\hat{\alpha}^+_i = 0$ a $0 < \hat{\alpha}^-_i < C$ : Tento případ odpovídá situaci, kdy bod $x_i$ leží pod spodním okrajem $\varepsilon$ pásmu, tj. $Y_i < \hat{Y}_i - \varepsilon$ .
$\hat{\alpha}^+_i = C$ a $\hat{\alpha}^-_i = 0$ : Tento případ odpovídá situaci, kdy bod $x_i$ leží na horním okrajem $\varepsilon$ pásmu, tj. $Y_i = \hat{Y}_i + \varepsilon$ .
$\hat{\alpha}^+_i = 0$ a $\hat{\alpha}^-_i = C$ : Tento případ odpovídá situaci, kdy bod $x_i$ leží na spodním okrajem $\varepsilon$ pásmu, tj. $Y_i = \hat{Y}_i - \varepsilon$ .

Tedy buď jsou oba koeficienty $\hat{\alpha}^+_i$ a $\hat{\alpha}^-_i$ nulové, nebo je pouze jeden z nich nenulový. Body $x_i$ , pro které je jeden z koeficientů $\hat{\alpha}^+_i$ a $\hat{\alpha}^-_i$ nenulový, se nazývají nosné body případně support vectors.

Určení $\hat{w}_0$ ¶

Pokud existuje takové $i = 1, . . . , N$ , že $0 < \hat{\alpha}^+_i < C$ nebo $0 < \hat{\alpha}^-_i < C$ , můžeme určit $\hat{w}_0$ podle případu:

Pokud $0 < \hat{\alpha}^+_i < C$ :

$\hat{w}_0 = Y_i - \sum_{j=1}^{N} (\hat{\alpha}^+_j - \hat{\alpha}^-_j) K(x_i, x_j) - \varepsilon$

Pokud $0 < \hat{\alpha}^-_i < C$ :

$\hat{w}_0 = Y_i - \sum_{j=1}^{N} (\hat{\alpha}^+_j - \hat{\alpha}^-_j) K(x_i, x_j) + \varepsilon$

Pokud takové $i$ neexistuje, $\hat{w}_0$ není jednoznačně určeno a může být zvoleno libovolně v rámci omezení, které znamenají:

pro $\hat{\alpha}^+_i = 0$ : $\hat{w}_0 \ge Y_i - \sum_{j=1}^{N} (\hat{\alpha}^+_j - \hat{\alpha}^-_j) K(x_i, x_j) - \varepsilon$
pro $\hat{\alpha}^-_i = 0$ : $\hat{w}_0 \le Y_i - \sum_{j=1}^{N} (\hat{\alpha}^+_j - \hat{\alpha}^-_j) K(x_i, x_j) + \varepsilon$
pro $\hat{\alpha}^+_i = C$ : $\hat{w}_0 \le Y_i - \sum_{j=1}^{N} (\hat{\alpha}^+_j - \hat{\alpha}^-_j) K(x_i, x_j) - \varepsilon$
pro $\hat{\alpha}^-_i = C$ : $\hat{w}_0 \ge Y_i - \sum_{j=1}^{N} (\hat{\alpha}^+_j - \hat{\alpha}^-_j) K(x_i, x_j) + \varepsilon$