Výpočet QR

Ortogonalni matice

Pro ortogonální matici $Q$ platí:

$$Q^TQ = I_n$$

Tvrzení 2.1: Je-li $Q \in \mathbb{R}^{m \times m}$ ortogonální matice, je její transpozice $Q^T$ také ortogonální matice.

Tvrzení 2.2: Pro ortogonální matice $Q_1, Q_2, . . . , Q_k \in \mathbb{R}^{m \times m}$, $m, k \in \mathbb{N}$, platí, že jejich součin je opět ortogonální matice, neboli $(Q_1Q_2 \dots Q_n)^T Q_1Q_2 \dots Q_n = I_m$.

Důkaz. Tvrzení plyne z vlastnosti ortogonálních matic a z faktu, že transpozice součinu matic je součin transpozic těchto matic, ale v obráceném pořadí:

$$(Q_1Q_2 \dots Q_k)^T = Q_k^T \dots Q_2^T Q_1^T$$

Z toho a z vlastnosti (2.1) ortogonálních matic získáváme $$\begin{align*} (Q_1Q_2 \dots Q_k)^TQ_1Q_2 \dots Q_k = \\ Q_k^T \dots Q_2^T (Q_1^T Q_1)Q_2 \dots Q_k = \\ Q_k^T \dots Q_2^T I_m Q_2 \dots Q_k = \\ \dots \\ Q_k^T Q_k = \\ I_m \end{align*}$$ Další vlastnost je již výše zmíněná klíčová vlastnost pro numerickou stabilitu, tedy že násobení ortogonální maticí nemění normu.

Tvrzení 2.3:

Je-li $Q \in \mathbb{R}^{m \times m}$ ortogonální matice, pak pro každý vektor $x \in \mathbb{R}^m$ platí $\|Qx\| = \|x\|$. Neboli násobení ortogonální maticí nemění normu.

Důkaz.

Důkaz je opět přímočarým použitím vlastnosti (2.1) a vlastností maticového násobení a Euklidovy normy: $\|Qx\|^2 = (Qx)^T Qx = x^T Q^T Qx = x^T x = \|x\|^2$.

QR rozklad

Mejme matici $A$ tu dokazeme rozlozit na:

$$A = QR$$ Kde Q je ortogonalni matice a r je horni trojuhelnikova, Coz muzeme znazornit:

$$A = QR = \begin{pmatrix} Q_L & Q_R \end{pmatrix} \begin{pmatrix} R_S \\ \Theta \end{pmatrix}$$

Po nasobeni na zbyde:

$$A = QR = Q_LR_S$$

Výpočet QR Rozkladu pomocí Givensových rotací

Jedním z přístupů k QR dekompozici je použití Givensůvých rotací. Givensův rotace jsou specifické ortogonální transformace, které vynulují specifický prvek matice a zachovávají ostatní.

Definice Givensův rotace vypadá následovně. Pro dva reálná čísla $a$ a $b$, Givensova rotace $G_{(i,j)}$, která vynuluje $b$ má tvar:

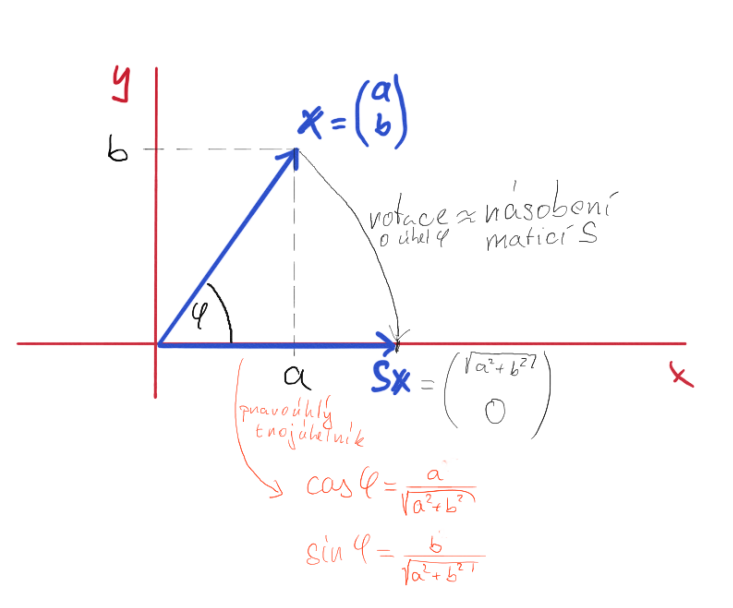$$G_{(i,j)} = \begin{pmatrix} \alpha & \beta \\ -\beta & \alpha \end{pmatrix},$$ kde

$$\alpha = \frac{a}{\sqrt{a^2 + b^2}}, \quad \beta = \frac{b}{\sqrt{a^2 + b^2}}.$$

Když chceme vynulovat prvek $a_{21}$, použijeme Givensovu rotaci $G_{(1,2)}$. Po vynulování prvku $a_{21}$ přejdeme na další prvek $a_{31}$ a použijeme Givensovu rotaci $G_{(1,3)}$.

Díky Givensůvým rotacím můžeme transformovat danou matici $A$ na horní trojúhelníkovou formu $R$. Tento proces lze přepsat jako $A = Q^T R$, kde $Q^T$ je transpozice matice $Q$. V případě Givensových rotací $Q^T$ je rovna součinu jednotlivých Givensových matic $G_{(i)}$,

$$Q^T = G_{(k)} G_{(k-1)} \cdots G_{(2)} G_{(1)},$$

a tedy

$$G_{(k)}^T G_{(k-1)}^T \cdots G_{(2)}^T G_{(1)}^T A=R.$$

Algoritmus

1. Krok: Vynulování $a_{21}$

Matici $A$ chceme přenásobit zleva maticí $G_{(1)}$ tak, aby byl prvek $a_{21}$ vynulován. Matici $G_{(1)}$ definujeme takto:

$$G_{(1)} = \begin{bmatrix} \alpha_{(1)} & \beta_{(1)} & 0 \\ -\beta_{(1)} & \alpha_{(1)} & 0 \\ 0 & 0 & 1 \\ \end{bmatrix}$$

Zde $\alpha_{(1)}$ a $\beta_{(1)}$ jsou určeny pomocí prvků, které chceme otočit:

$$\alpha_{(1)} = \frac{a_{11}}{\sqrt{a_{11}^2 + a_{21}^2}} \quad \text{a} \quad \beta_{(1)} = \frac{a_{21}}{\sqrt{a_{11}^2 + a_{21}^2}}$$

1. Krok: Vynulování $a_{31}$

Nyní máme matici $A'$, která vypadá takto:

$$A' = \begin{bmatrix} a'_{11} & a'_{12} & a'_{13} \\ 0 & a'_{22} & a'_{23} \\ a'_{31} & a'_{32} & a'_{33} \\ \end{bmatrix}$$

Chceme vynulovat prvek $a'_{31}$. Matici $A'$ chceme přenásobit zleva maticí $G_{(2)}$ tak, aby byl prvek $a'_{31}$ vynulován. Matici $G_{(2)}$ definujeme takto:

$$G_{(2)} = \begin{bmatrix} \alpha_{(2)} & 0 & \beta_{(2)} \\ 0 & 1 & 0 \\ -\beta_{(2)} & 0 & \alpha_{(2)} \\ \end{bmatrix}$$

Zde $\alpha_{(2)}$ a $\beta_{(2)}$ jsou určeny pomocí prvků, které chceme otočit:

$$\alpha_{(2)} = \frac{a\prime_{11}}{\sqrt{a\prime_{11}^2 + a\prime_{31}^2}} \quad \text{a} \quad \beta_{(2)} = \frac{a\prime_{31}}{\sqrt{a\prime_{11}^2 + a\prime_{31}^2}}$$

Nyní máme matici $A''$, která vypadá takto:

$$A'' = \begin{bmatrix} a''_{11} & a''_{12} & a''_{13} \\ 0 & a''_{22} & a''_{23} \\ 0 & a''_{32} & a''_{33} \\ \end{bmatrix}$$

Tato matice má prvky $a''_{21}$ a $a''_{31}$ rovny nule atd.

Výpočet QR rozkladu pomocí Householderových reflexí

Budeme tedy hledat ortogonální matice (budeme je značit $P$), pro které platí

$$P\mathbf{x} = P \begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \\ \end{pmatrix} = \begin{pmatrix} \pm ||x|| \\ 0 \\ \vdots \\ 0 \\ \end{pmatrix}$$ Pro nadrovinu musi platit: $$u^Tx=0$$ Chceme udelat nasledujici:

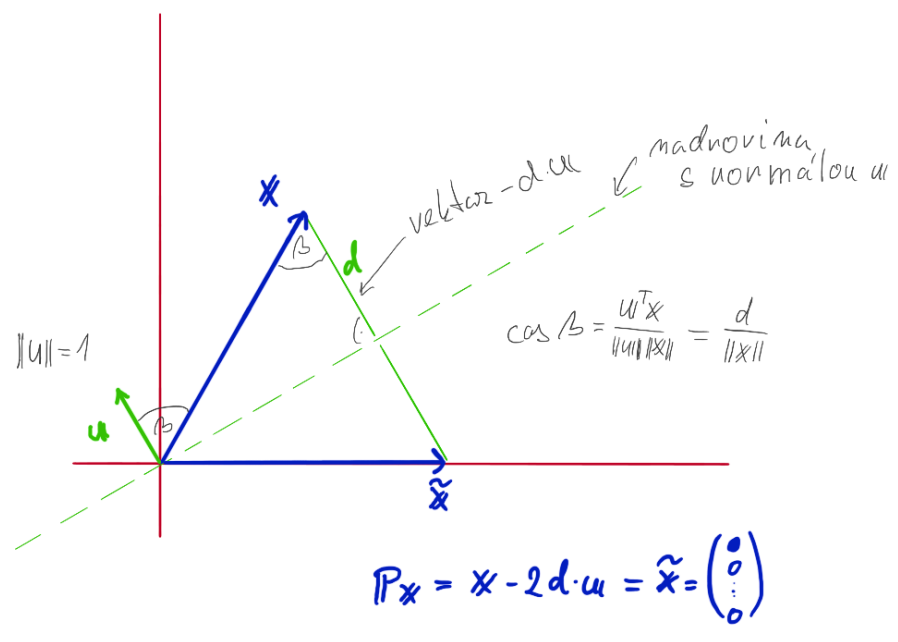
Abychom dostali takovyto zrcadlovy obraz musime udelat: $$x = \tilde{x} = x - 2du.$$ Z goniometrie jeste vime: $$cos(\beta) = \frac{u^Tx}{||u||\ ||x||} = \frac{d}{||x||}$$ Z toho plyne (nezapomenme ze $||u||=1$): $$d=u^Tx$$ Coz muzeme dosadit: $$\tilde{x} = x-2du=x-2u^Txu=x-2uu^Tx=(I_N-2uu^T)x=Px$$ Vime tedy ze: $$P=I_N-2uu^T$$ .... dalsi postup je ve scriptech

QR algoritmus, Hessenbergova forma matice

QR algoritmus slouzi k najiti vlastnich cisel. Cele to stoji na tom ze podobne matice maji stejna vlastni cisla.

Nezapomenme ze pro ortogonalni matici $Q$ plati $Q^T=Q^{-1}$

Mějme tedy čtvercovou matici $A ∈ R^{n,n}$, u které hledáme vlastní čísla. Muzeme rict ze matice $A$ je podobna matici $RQ$ protoze: $$A = QR \Rightarrow R=Q^{-1}A \Rightarrow R = Q^TA \Rightarrow RQ = Q^TAQ$$

Algoritmus je následující:

1. Vypočítejte QR rozklad matice $A$: $A = QR$.
2. Vypočítejte novou matici $A' = RQ$.

Tyto kroky se opakují, dokud se matice $A'$ neaproximuje k diagonální matici. Taková konvergence se dá ještě dost zrychlit prevedenim matice a na Hessenbergovu formu.

Hessenbergova forma matice

Matice $A \in \mathbb{R}^{n \times n}$ je v Hessenbergově formě, pokud $a_{ij}=0$ pro všechny $i>j+1$. Matice A je navíc tridiagonální, jestliže pro $1 ≤ i, j, ≤ n$ platí : $(i > j + 1 \text{ nebo } i < j − 1) ⇒ Ai,j = 0$ Matice je triagonalni pokud matice $A$ je symetricka, matice $P$ je vzdy symetricka a take ortogonalni

Proc Hessenbergova forma je podobna matici $A$

Kdyz bychom chteli zformulovat poddobnou matici k matici $A$ muzeme se kouknout na to jak vytvarime $QR$ rozklad, kdyz pouzivame householderovy reflexe sestrojujeme: $$P_1A= P_1 \begin{pmatrix} \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet \\ \end{pmatrix} = \begin{pmatrix} \alpha & \bullet & \bullet & \bullet \\ 0 & \bullet & \bullet & \bullet \\ 0 & \bullet & \bullet & \bullet \\ 0 & \bullet & \bullet & \bullet \\ \end{pmatrix}$$ Kdyz bychom ale chteli zkusit vynasobit matici $A$ i z prava narazime na to ze vytvorene nuly muzou zmizet. Problém je ten, že v prvním sloupci matice $P_1AP_1$ jsou pod diagonálou součiny typu:

$$\begin{pmatrix} 0 & \bullet & \bullet & \bullet \\ \end{pmatrix} \begin{pmatrix} 1-u_1^2 \\ u_1u_2 \\ u_1u_3 \\ u_1u_4 \\ \end{pmatrix} = \begin{pmatrix} \bullet \\ \end{pmatrix}$$ Pouzijeme tedy matici o jednu mensi tedy: $$P_1 = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & & &\\ 0 & &I_N-2uu^T &\\ 0 & & &\\ \end{pmatrix}$$ Z toho nam vyjde:

$$P_1 \begin{pmatrix} \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet \\ \bullet & \bullet & \bullet & \bullet \\ \end{pmatrix} P_1= \begin{pmatrix} \bullet & \bullet & \bullet & \bullet \\ \alpha & \bullet & \bullet & \bullet \\ 0 & \bullet & \bullet & \bullet \\ 0 & \bullet & \bullet & \bullet \\ \end{pmatrix} P_1= \begin{pmatrix} \bullet & \bullet & \bullet & \bullet \\ \alpha & \bullet & \bullet & \bullet \\ 0 & \bullet & \bullet & \bullet \\ 0 & \bullet & \bullet & \bullet \\ \end{pmatrix}$$ Pokud takhle budeme postupovat az budeme mit vynulovane cisla pod poddiagonalou a vytvorime tim Hessenbergovu formu matice mame tu matici podobnou.

Potom muzeme pouzit Givensovske rotacce n-1 krat a ziskame qr rozklad. Je to potom vypocetne velice rychle

Alogritmus

1. Matici $A^TA$ převedeme pomocí $n−2$ matic $P_i$ provádějících Householderovy reflexe na podobnou matici $B$, která je tridiagonální.
2. Na matici $B_0 = B$ pak aplikujeme QR algoritmus.
3. Najdeme QR rozklad $B_0 = Q_0R_0$, ten můžeme najít pomocí $n − 1$ Givensových rotací, které nulují $n − 1$ prvků pod diagonálou. Násobení maticí provádějících Givensovu rotaci vždy ovlivňuje pouze 6 prvků matice a je tedy výpočetně nenáročné.
4. Dále pak konstruujeme posloupnost matic $(B_i)_{i≥1}$ takto: $B_i = R_{i−1}Q_{i−1}$ a její QR rozklad označíme $B_i = Q_iR_i$ .