10. Systémy hromadné obsluhy a jejich limitní vlastnosti. Souvislost s Markovskými řetězci se spojitým časem. (NI-VSM)¶

Poissonový process¶

Jedna se o náhodný čítací proces s nezávislými exponenciálně rozdělenými časy mezi událostmi.

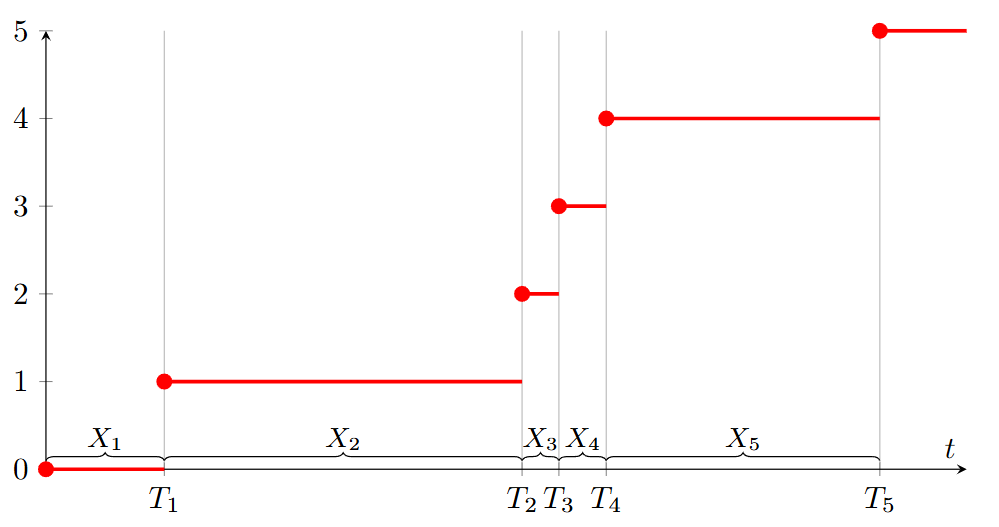
Pasted image 20250119141930.png

Bud $\{X_j|j\in\mathbb{N}\}$ nezávislý stejně rozdělený process s exponenciálním rozdělením: $\text{Exp}(\alpha)$
- První definujeme kolik casu je potřeba do příchodu -té události jako tedy náhodný process : $T_0=0\quad\quad T_n=T_{n-1}+X_n=\sum_{j=1}^nX_j\quad n\geq 1$
- Poté můžeme definovat Poissonův process jako : $N_t(\omega) = \max\{n\in\mathbb{N}|T_n(\omega)\leq t\}$

Exponenciální závody¶

Nezáleží, jak dlouho běží, pouze, jaký je aktuální stav
V případě výhry jednoho, druhý čas se zkracuje, ale zůstává nezávislý (bezpamětnost Poissonova procesu)

Hromadná obsluha¶

Model hromadné obsluhy¶

Založeno na teorii front
Slouží k modelování systémů postavených na požadavcích a jejich odbavování
- Např. odbavování zákazníků u pokladen, zpracovávání paketů ve switchích, obsluha požadavků na serveru
Požadavky přichází podle určitého procesu
Každý server může obsluhovat pouze jeden požadavek v jednu chvíli
Můžeme mít více serverů
Před serverem se tvoří fronta požadavků čekajících na obsloužení

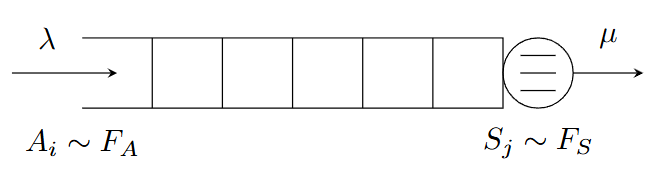
Pasted image 20250119175852.png

$λ$ (zákazníků za časovou jednotku) = intenzita příchodů
= náhodný čas mezi příchodem -ního a -tého zákazníka $A_i \sim F_A\quad \quad \quad EA_i = \frac{1}{\lambda}$ kde $F_A$ je nějaké náhodné rozděleni příchodu zákazníků
$μ$ (zákazníků za časovou jednotku) = intenzita obsluhy jednoho serveru
= čas obsluhy -tého zákazníka $S_j \sim F_S,\quad\quad\quad ES_j=\frac{1}{\lambda}$ kde $F_S$ je nějaké náhodné rozděleni zpracovaní zákazníků
Veličiny $A_1, A_2, . . . , S_1, S_2, . . .$ jsou nezávislé.
Server obsahuje $c$ nezávislých obslužných míst.

Proces hromadné obsluhy¶

Jedna se o process který modeluje počet zákazníků ve frontě
- $X=\{X_t|t\geq 0\}$ kde $t:$ určuje čas
Intenzita příchodů je $λ$ .
Intenzita obsluhy zákazníků je nejvýše $cμ$ .
- $c:$ Počet obslužných mist
- $\mu:$ Intenzita obsluhy
Můžeme zjistit co "vyhraje": podmínka existence stacionárního rozděleni
- $\varrho = \frac{\lambda}{c\mu}$
- Je-li $\varrho > 1$ , počet zákazníků v systému poroste nade všechny meze
- Je-li $\varrho < 1$ , ustálí se systém na stabilním rovnovážném rozdělení.

Kendallova notace¶

Jedna se o zápis modelu hromadné obsluhy

$A|S|c\ (|K|N|D)$

$A$ – rozdělení časů příchodu $F_A$ ,
$S$ – rozdělení časů obsluhy $F_S$ ,
$c$ – počet obslužných míst,
$K$ – kapacita systému (pokud neuvedeno, je rovna $+∞$ ),
$N$ – velikost populace (pokud neuvedeno, je rovna $+∞$ ),
$D$ – typ obsluhy (pokud neuvedeno, je rovna FIFO).

Rozdělení A a S jsou značena:

$M$ , $M(λ)$ – exponenciální rozdělení (markovské),
$D$ , $D(d)$ – degenerované rozdělení, soustředěné v hodnotě $d$ ,
$G$ – obecné rozdělení, neznámé, nebo známé „neexponenciální“.

Littleho veta¶

Věta která popisuje vztah mezi jednotlivými parametry systému tedy:
Věta říká, že střední počet položek v systému je roven intenzitě příchodů vynásobené průměrným časem stráveným v systému. $EN=\lambda\cdot ET$

Druhy systémů hromadné obsluhy¶

(M|M|1)¶

Jedna se o process s exponenciálním rozdělením jak u příchodu tak i u obsluhy kde je pouze jedno obslužné misto
$λ_n = λ , n ∈ N_0 , μ_m = μ , m ∈ N$
Matice intenzit je:

$Q = \begin{pmatrix} -\lambda & \lambda & 0 & 0 & \cdots \\ \mu & -(\lambda + \mu) & \lambda & 0 & \cdots \\ 0 & \mu & -(\lambda + \mu) & \lambda & \cdots \\ 0 & 0 & \vdots & \vdots & \ddots \end{pmatrix}$

Stacionární rozdělení:
- Existuje pouze pokud $\lambda<\mu$
- $π_n = (1 −\frac{\lambda}{\mu})(\frac{\lambda}{\mu})^n$
Doba čekání ve frontě
- Nečeká se, pokud je server prázdný
- Jinak čeká přibližně $\text{Exp}(\mu-\lambda)$

(M|M|∞)¶

Jedna se o process s exponenciálním rozdělením jak u příchodu tak i u obsluhy kde je nekonečno obslužných míst
$λ_n = λ , n ∈ N_0 , μ_m = μ , m ∈ N$
Matice intenzit je:

$Q = \begin{pmatrix} -\lambda & \lambda & 0 & 0 & 0 & \cdots \\ \mu & -(\lambda + \mu) & \lambda & 0 & 0 & \cdots \\ 0 & 2\mu & -(\lambda + 2\mu) & \lambda & 0 & \cdots \\ 0 & 0 & 3\mu & -(\lambda + 3\mu) & \lambda & \cdots \\ 0 & 0 & 0 & \vdots & \vdots & \ddots \end{pmatrix}$

Stacionární rozdělení:
- Vždy existuje
- $π_n = \text{Pois}(\frac{\lambda}{\mu})$
Doba čekání ve frontě
- Nečeká se. Vždy je obslužné misto volné

(M|M|c)¶

Jedna se o process s exponenciálním rozdělením jak u příchodu tak i u obsluhy kde je $c$ obslužných mist
Jsou-li všechna obsazená, zařadí se zákazník do fronty.
$λ_n = λ , n ∈ N_0 , μ_m = μ , m ∈ N$
Matice intenzit je:
- Tedy od naplněnosti $c$ se už nebude zvyšovat počet obslužných mist
Stacionární rozdělení:
- Existuje pouze pokud $\lambda<\mu$
- $π_n = (\frac{\lambda}{\mu})\frac{1}{\min\{n,c\}}\pi_{n-1}$

Souvislost s Markovskými řetězci se spojitým časem¶

Hromadná obsluha využívá Poissonův proces pro příjem a odbavování požadavků, zachovává se bezpaměťovost
Systémy lze vyjádřit pomocí matic intenzity spojitého markovského procesu