11. Význam tříd NP a NPH pro praktické výpočty. (NI-KOP)¶

Kombinatorické problémy¶

Kombinatorická matematika:
- Lze vyzkoušet všechny kombinace v konečnem case a rozhodnout o problému
Charakterizace problému:
- Vstupní proměnné
- Výstupní proměnné
- Konfigurační proměnné
  - To, co vyjádří všechny „kombinace“
- Omezení
- Optimalizační kritérium
  - MIN, MAX,...
Typy problémů:
- Rozhodovací problém: Existuje $Y$ takové, že $R(I, Y)$ ?
- Konstruktivní problém: Sestrojit nějaké $Y$ takové, že $R(I, Y)$ .
- Enumerační problém: Sestrojit všechna $Y$ taková, že $R(I, Y)$ .
- Početní problém: Kolik je $Y$ takových, že $R(I, Y)$ .
Optimalizační problem: Jedna se o stejné problémy definované výše pouze s nějakou optimalizační podmínkou
- MIN / MAX / Lepší než ...
Základní pojmy:
- Konfigurace je ohodnocení konfiguračních proměnných
- Řešení je konfigurace, která vyhovuje omezujícím podmínkám
- Optimální řešení je řešení, které má nejlepší hodnotu optimalizačního kritéria
- Suboptimální řešení je řešení, které má přijatelnou hodnotu optimalizačního kritéria

Turingův stroj¶

Jedna se o teoreticky model počítače
Deterministický Turingův stroj s jednou páskou je osmice $(Q,Σ,Γ,b,δ,q_0,q_{ANO},q_{NE})$ :
- $Q$ je konečná množina vnitřních stavů,
- $Σ$ je konečná vstupní abeceda (obvykle $Σ=\{0,1\}$ ),
- $Γ$ je konečná abeceda pásky, $Σ⊂Γ$ ,
- $b$ je prázdný symbol (blank), $b∈Γ∖Σ$ – obvykle $b=⊔$ ,
- Deterministicky Turingův stroj:
  - $δ$ je zobrazenı́ z množiny $Q×Γ$ do množiny $Q×Γ×\{←,∙,→\}$ , které na základě aktuálního vnitřního stavu a aktuálně čtených symbolů na pásce určı́, jaký má být nový vnitřní stav, jaké symboly se mají zapsat na pásku a jakým směrem se má hlava pohnout;
- Nedeterministicky Turingův stroj
  - $δ$ je relace mezi množinami $Q×Γ$ a $Q×Γ×{←,∙,→}$ , které na základě aktuálního vnitřního stavu a aktuálně čtených symbolů na jednotlivých páskách určı́, jaké kombinace nového vnitřního stavu, jaké symbolů zapsaných na pásku a směru pohybu hlavy mohou následovat; je tedy $δ⊆Q×Γ×Q×Γ×{←,∙,→}$ ;
- $q_0$ je počáteční stav, $q_0\in Q$ ;
- $q_{ANO}$ a $q_{NE}$ jsou koncové stavy, $q_{ANO},q_{NE} \in Q$ .

Třídy PSPACE, EXPTIME¶

Rozhodovací problém patří do třídy PSPACE, jestliže pro něj existuje program pro deterministický Turingův stroj, který jej řeší v paměti $O(n^k)$ , kde $n$ je velikost instance a $k$ konečné číslo.
Rozhodovací problém patří do třídy EXPTIME, jestliže pro něj existuje program pro deterministický Turingův stroj, který jej řeší v čase $O(2^{P(n)})$ , kde $P(n)$ je polynom ve velikosti instance $n$ .

Třídy Složitosti problémů¶

Important

Pasted image 20250120181452.png

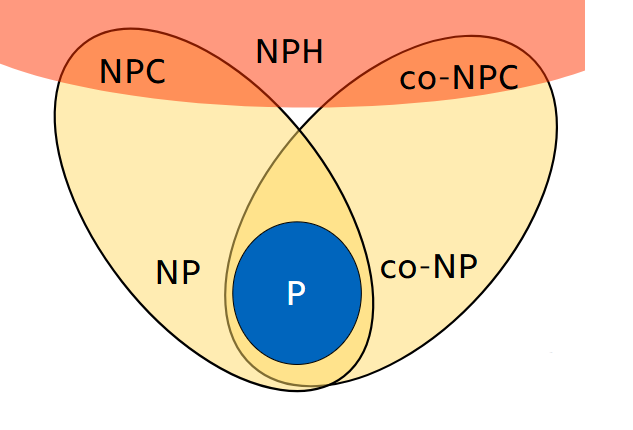
P (Polynomial Time)
- Třída problémů řešitelných deterministickým Turingovým strojem v polynomiálním čase
- Problémy s efektivním algoritmickým řešením
- Lze vyřešit v čase $O(n^k)$ , kde $k$ je konstanta

Important

NP (Nondeterministic Polynomial Time)
- Třída problémů, jejichž řešení lze ověřit v polynomiálním čase
- Lze vyřešit nedeterministickým Turingovým strojem v polynomiálním čase $O(n^k)$
- Řešeni deterministickým Turingovým je v exponenciálním čase: $2^{O(T(n))}$ Kde $T(n)$ je složitost algoritmu v nedeterministickém TS
- Platí: $P \subseteq NP$
- Otevřená otázka: $P \stackrel{?}{=} NP$
- Kontrola / Certifikát zda výstupní konfigurace je rosením problému je problem patrici do P
- Každý NP problem jde převést na SAT
- Kratky svědek: Výsledek který ověří ze konfigurace je řešením problému
- co-NP
  - Třída problémů, kde lze v polynomiálním čase ověřit negativní odpověď
  - Doplněk třídy NP
  - Otevřená otázka: Zda $NP = co-NP$
  - Maji dlouhé svědky:
    - Neexistuje číslo vetší jak 10
    - Svědkové jsou všechny čísla která nejsou věsti jak 10
NPC (NP-Complete)
- Nejtěžší problémy v třídě NP
- Každý problém v NP lze na ně převést v polynomiálním čase
- Řešení jednoho NP-Complete problému by znamenalo řešení všech problémů v NP
- Kontrola / Certifikát zda výstupní konfigurace je rosením problému je problem patrici do P
NPH (NP-Hard)
- Problémy minimálně tak těžké jako nejtěžší problémy v NP
- Kontrola / Certifikát zda výstupní konfigurace je řešením problému je problem patrici do NP
- Nemusí být nutně v NP
- Příklad: Problém zastavení (Halting problem)

NPI
- Problémy v NP, které nejsou v P nebo NPC
- Existuje pouze pokud $P \neq NP$
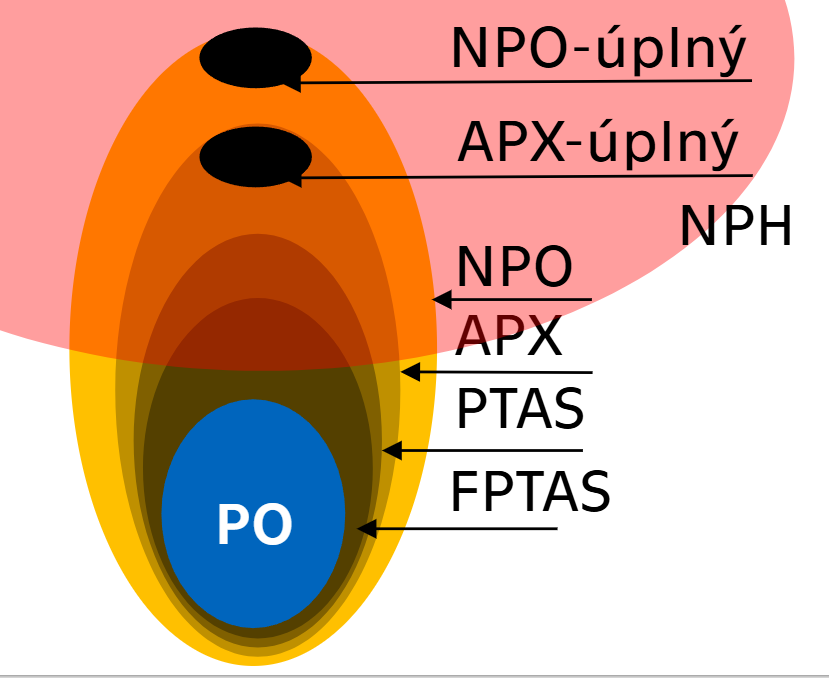
PO a NPO
- Optimalizační varianty rozhodovacích problémů
- Hledají nejlepší řešení místo binární odpovědi ano/ne
- Často výpočetně náročnější než jejich rozhodovací protějšky

Important

Pasted image 20250120183700.png

Redukce algoritmu¶

Karpova redukce¶

Rozhodovací problém $Π_1$ je Karp-redukovatelný na $Π_2 (Π_1 ∝ Π_2)$ , jestliže existuje polynomiální program pro (deterministický) Turingův stroj, který převede každou instanci $I_1$ problému $Π_1$ na instanci $I_2$ problému $Π_2$ tak, že výstup obou instancí je shodný.

Turingova redukce¶

Problém $Π_1$ je Turing-redukovatelný na $Π_2$ ( $Π_1$ ∝ $Π_2$ ), jestliže existuje program pro (deterministický) Turingův stroj, který řeší každou instanci $I_1$ problému $Π_1$ tak, že používá program $M_2$ pro problém $Π_2$ jako podprogram (jehož trvání považujeme za jeden krok).

Klíčový rozdíl:

Karpova redukce je speciálním případem Turingovy redukce
Karpova redukce vyžaduje polynomiální převod

Význam pro praktické výpočty¶

Important

NP a NPH problémy nelze efektivně řešit – řešení je exponenciální, které pro větší instance může trvat neakceptovatelně dlouho – využití v kryptografii, hashování.
Neznámé problémy můžeme redukcí převádět na známé problémy a řešit je dle zvyku.
Např. mnohé úlohy převádíme na SAT problém splnitelnosti.
NPH: Kontrola / Certifikát zda výstupní konfigurace je řešením problému je problem patrici do NP
NPH: Jsou extrémně výpočetně náročné problémy.
NPH: Nemusíme byt schopni je převést na SAT problémy
NPO: Můžeme použít aproximační algoritmy k jejich řešeni.
Metoda redukce stavového prostoru – např. branch and bound – nepoužitelné výsledky ignorovány
Aproximace: jednodušší heuristiky (simulované ochlazování, genetika) pro přibližné řešení

Aproximativní algoritmy¶

Pasted image 20250120200610.png

Aproximativní algoritmus¶

Algoritmus pro optimalizační problémy, který nachází řešení blízké optimálnímu
Garantuje maximální odchylku od optimálního řešení
Používá se pro NP-těžké problémy, kde přesné řešení je výpočetně náročné

Třída APX¶

Množina optimalizačních problémů s konstantně aproximovaným řešením
Existuje algoritmus, který najde řešení s garantovanou aproximační konstantou
Příklad: Problém obchodního cestujícího s aproximací $\leq 2$
Sbírka problémů, kde umíme zaručit, že naše řešení bude maximálně 2x horší než to nejlepší možné

PTAS (Polynomial Time Approximation Scheme)¶

Algoritmus, který pro libovolné $\epsilon > 0$ najde $(1+\epsilon)$ -aproximační řešení
Doba běhu je polynomiální vzhledem k velikosti vstupu a $\frac{1}{\epsilon}$
Algoritmus, který ti umožní nastavit, jak moc přesné řešení chceš. Čím přesnější, tím déle počítá

FPTAS (Fully Polynomial Time Approximation Scheme)¶

Speciální případ PTAS
Doba běhu je polynomiální vzhledem k velikosti vstupu a $\frac{1}{\epsilon}$

Pseudopolynomiální algoritmus¶

Algoritmus s polynomiální složitostí vzhledem k numerické hodnotě vstupu
Složitost závisí na hodnotách čísel, nikoliv jejich délce
Prakticky použitelný jen pro malé číselné hodnoty

Rozhodovací problém splnitelnosti Booleovy CNF formule (SAT)¶

Definice problému¶

Vstup:

Množina $X$ o $n$ proměnných $\{x_1, \ldots, x_n\}$ , kde $x_i \in \{0,1\}$
Booleova formule $F$ v konjunktivní normální formě o $m$ klauzulích

Úkol:

Rozhodnout, zda existuje ohodnocení $Y$ proměnných $X$ takové, že $F(Y) = 1$

Příklad¶

Pro $n = 4, m = 6$ :

$F = (x_1 + \neg x_3 + x_4).(\neg x_1 + x_2 + \neg x_3).(x_3 + x_4).(x_1 + x_2 + \neg x_3 + \neg x_4).(\neg x_2 + x_3).(\neg x_3 + \neg x_4)$

Řešení:

$Y_1 = (0, 0, 0, 1)$
$Y_2 = (1, 0, 0, 1)$
$Y_3 = (1, 1, 1, 0)$

Výstup: Ano, formule je splnitelná