12. Experimentální vyhodnocení algoritmů, zejména randomizovaných. (NI-KOP)¶

Experimentální vyhodnocení¶

Používá se pro zjištění kvality nebo výpočetní náročnosti
- Většinou srovnáváme dva algoritmy a porovnáváme jejich metriky
Pro známe problémy existuji benchmarky např: SAT
Primární metriky
- Počet kroků
- Úspěch (ano-ne)
- Optimalizační kritérium - jeho hodnota
Sekundární metriky na jedné instanci: potlačení variance od RNG
- Statistické rozdělení počtu kroků
- Pravděpodobnost, že algoritmus skončil
  - do daného kroku - distribuční funkce
  - úspěšně do daného kroku - korigovaná distribuční funkce
  - úspěšně do daného kroku s hodnotou opt. kritéria alespoň K
    - distribuční funkce korigovaná na práh K

Postup při experimentu¶

Položíme otázky které chceme zjistit
- Otázka algoritmu musí být významná
Vytvoříme plan experimentu
- Navržený experiment musí být přesvědčivý pro zodpovězení té otázky
Provedeme experiment
- Provedení experimentu musí být opakovatelné, aby:
  - K experimentu byla důvěra a výsledky byly přijaty
  - Výsledky byly použitelné pro další výzkum
Posbíráme data
- Sběr dat a jejich prezentace musí umožnit
  - Alternativní interpretaci
  - Použití pro další výzkum
Interpretujeme výsledky a odpovíme na otázky
- Interpretace a prezentace odpovědi musí zajistit, aby
  - K experimentu byla důvěra a výsledky byly přijaty

Zdroje variance v experimentech¶

Generator
- Máme-li experiment kde generujeme data pomoci náhodného generátoru dává nám to zdroj variance v experimentu který následně budeme muset řešit
Náhodná Perturbace
- Tento typ variance přehazuje pořadí dat tak aby testoval (většinou) robustnost algoritmu
Algoritmus
- Samotný algoritmus může byt randomizovaný (opak deterministického) tedy při vstupu stejných dat může byt výsledek malinko jiny
  - Evoluční algoritmus
  - Las Vegas/Monte Carlo
  - Simulované ochlazovaní
Žádná variance
- V případě ze nedokážeme generovat žádnou z daných varianci můžeme využít standartní sadu instanci.(Benchmark) Který bud seženeme nebo vytvoříme

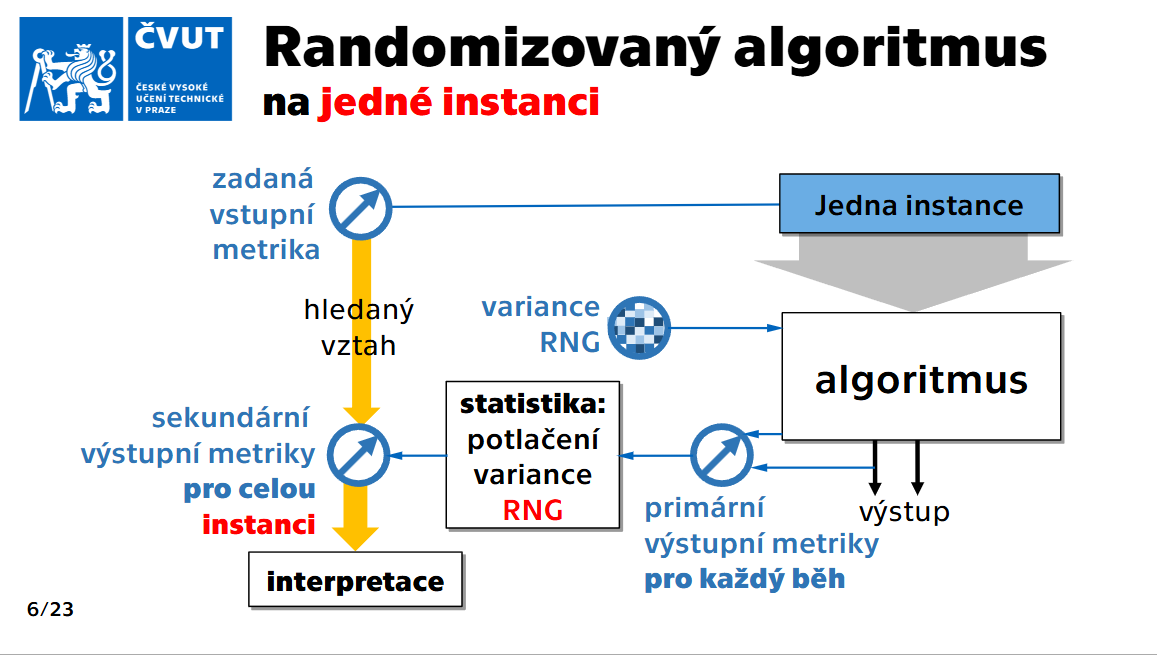
Řešení variance v testech¶

Při analýze variance v experimentálním designu je klíčové dodržovat systematický postup řešení. Vždy se začíná řešením variance posledního zdroje a postupuje se směrem nahoru. V případě všech 3 zdrojů varianci použijeme následující postup:

Randomizovaný algoritmus
- Potlačení vnitřních variancí
- Minimalizace náhodných vlivů uvnitř algoritmu
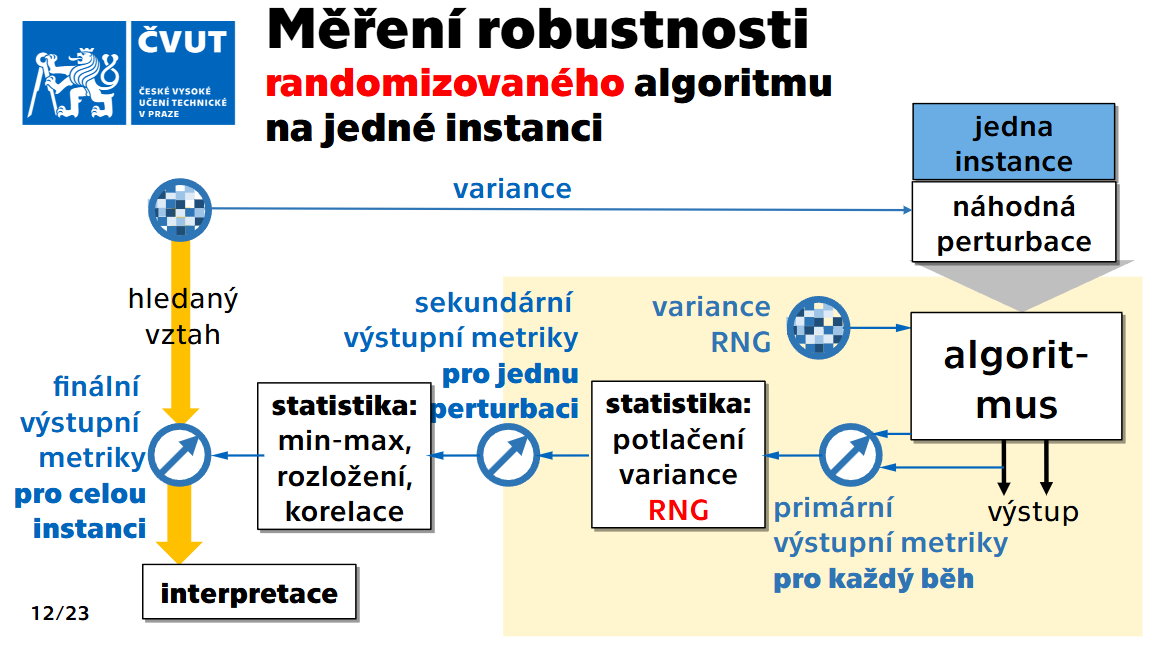
Náhodná perturbace
- Analýza statistických charakteristik:
  - Minimální a maximální hodnoty
  - Rozložení dat
  - Korelační vztahy
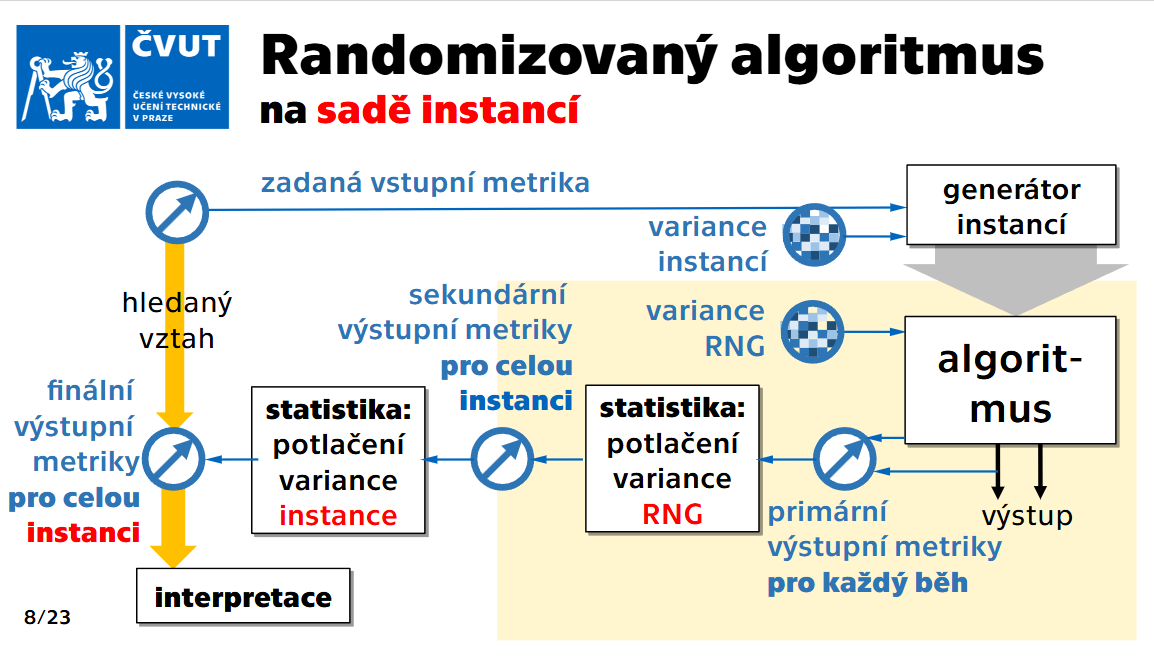
Generator instancí
- Vyhodnocení nashromážděných statistik
- Potlačení variancí v generování vstupních dat

Příklady testů¶

Pasted image 20250120214243.png

Pasted image 20250120214132.png

Pasted image 20250120214210.png

Typy testů¶

White box
- omezená sada instancí
- detailní měření (i vnitřního stavu)
- porozumění fungování heuristiky
- modifikace heuristiky během měření
Black box
- plná sada instancí
- měření statistických výsledků
- ověření kvality a výkonu
- žádné modifikace heuristiky

Randomizované algoritmy¶

Algoritmus je založen na náhodné volbě
Výhody
- Strukturní jednoduchost
- Nezávislým opakováním se dá zlepšit kvalita
- Očekávaná kvalita výsledku může být lepší než zaručená kvalita aproximativních algoritmů

Monte Carlo¶

MAX_EFFORT = CONSTANT
for (i=1; i<=MAX_EFFORT; i++) {
    hrst = random (1, kupka.size());
    if (kupka[hrst] == jehla) return True;
}
return False;

Založen na principu ze effort je staticky.
- S nějakou pravděpodobností se dobereme k výsledku
Pravděpodobnost správného výsledku je náhodná proměnná

Las Vegas¶

order = random_permutation (1, kupka.size());
foreach (hrst in order) {
    if (kupka[hrst] == jehla) return True;
}
return False;

Založen na principu ze počet kroku je náhodná proměnná.
- Vždy se dobereme k výsledku
Počet kroků je náhodná proměnná