16. Výkonnostní měřítka paralelních algoritmů, PRAM model, APRAM model, škálovatelnost. (NI-PDP)

---

Výkonnostní měřítka paralelních algoritmů

Big O notace

• Horní mez: $O(*)$
• Dolní mez: $\Omega(*)$
• Těsná mez: $\Theta(*)$

Sekvenční měřítka

• Časová složitost/doba výpočtu sekvenčního algoritmu: $T_A^K(n)$

  • Sekvenční algoritmus $A$, který řeší problém $K$ na vstupních datech velikosti $n$

• Spodní mez sekvenční časové složitosti: $SL^K(n)$

  • Nejhorší časová složitost nejlepšího možného sekvenčního algoritmu pro problem $K$

• Horní mez sekvenční časové složitosti: $SU^K(n)$

  • Nejhorší časová složitost nejrychlejšího existujícího sekvenčního algoritmu pro problem $K$
• Asymptoticky optimální sekvenční algoritmus: $T_A(n)=\Theta(SU^K(n))=\Theta(SL^K(n))$
  • Když těsná mez nejlepšího možného a nejrychlejšího existujícího algoritmu se rovná

Paralelní měřítka

• Paralelní časová složitost závisí ne jenom na velikosti dat ale i na počtu procesorů/vláken $p$
• Paralelní čas:
  • $T(n,p)$
  • Čas který uplynul od začátku paralelního vypočtu do konce vypočtu posledního procesoru
  • Spodní mez na paralelní čas
    • $L^K(n,p)=\frac{SL^K(n)}{p}$
• Paralelní cena
  • $C(n,p) = p \times T(n,p)$
  • Součin počtu procesorů a celkového výpočetního času
    • Snažíme se minimalizovat nevyužitý výpočetní čas
    • Horní mez: Sekvenční řešení
  • Optimální cena
    • Procesory jsou plně využity, optimum je sekvenční alg
    • $C(n,p)=O(SU(n))$
• Paralelní zrychleni
  • $S(n,p)=\frac {SU(n)}{T(n,p)}$
  • Poměr doby běhu sekvenčního a paralelního algoritmu
  • Ideální cíl: Lineární zrychlení
    • Počet procesorů = dosažené zrychlení
    • $S(n,p)=\Omega(p)$
  • Super lineární zrychlení
    • Zrychleni je vetší než počet procesorů
    • Obvykle hardwarový efekt
• Paralelní efektivnost
  • $E(n,p)=\frac{SU(n)}{C(n,p)} \leq 1$
  • Podíl nejlepšího sekvenčního řešení k ceně paralelního řešení
  • Jedna se vlastně o zrychleni na jádro
  • Konstantní efektivnost
    • Je li efektivnost vždy vetší než nějaká konstanta
    • $E(n,p)\geq E_0$
    • Asymptoticky $E(n,p) = \Omega(1)$
• Paralelní optimalita výkonu
  • Hledáme li optimální paralelní algoritmus stačí nám pouze jeden cílů
  • cenově optimální $\Leftrightarrow$ lineární zrychlení $\Leftrightarrow$ konstantní efektivnost

Paralelní binární redukce

• Snažíme se sečíst všechny prvky v poli
• Algoritmus
  1. Všechny procesory jsou aktivní
  2. Každý lichý processor $P_i$ posle svoji hodnotu procesoru $P_{i-1}$ a procesor se zneaktivni
  3. Processor který dostal hodnotu ji sečte se svoji hodnotou
  4. Toto se opakuje do získaní výsledku v procesoru $P_0$

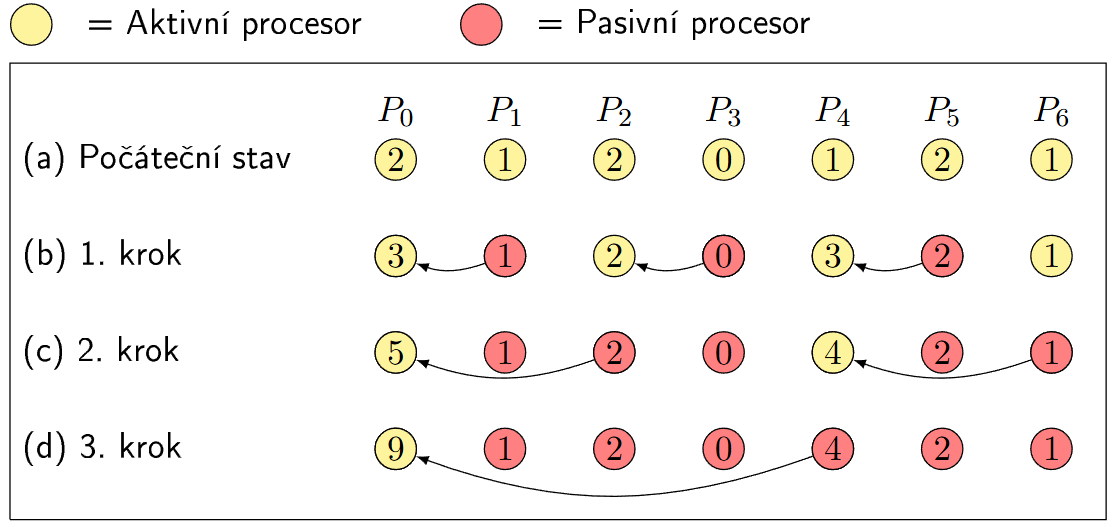
• Analýza složitosti pro $n$ prvku a $n$ procesoru

Charakteristika	Sekvenční	Paralelní
Spodní mez složitosti $SL(n)$	$\Theta(n)$	$\Theta(n)$
Horní mez složitosti $SU(n)$	$\Theta(n)$	$\Theta(n/\log n)$
Čas výpočtu $T(n,n)$	$\Theta(n)$	$\Theta(\log n)$
Efektivita $E(n,n)$	-	$\Theta(1/\log n)$
Cena $C(n,n)$	-	$\Theta(n \log n)$

PRAM

• Jedná se o výpočetní model Paralel Random Access Machine PRAM
• Máme $p$ procesorů kde každý procesor ma vlastní lokální soukromou paměť
• Máme $M$ sídelních paměťových buněk (pole)
• Procesor ma 3 synchronií operace
  • Read - Ctění z sdílené paměti
  • Write - Zápis do sdílené paměti
  • Local - Lokální operace
• Přístup do sdílené paměti je v case $O(1)$
• Procesory komunikuji přes zápis / ctění do / z sdílené paměti
• Řešení konfliktů při zápisu do sdílené paměti
  • Exclusive Read Exclusive Write (EREW)
    • Nesmí se číst ani zapisovat současně
  • Concurrent Read Exclusive Write (CREW)
    • Smí se paralelně číst ale zápis pouze jeden
  • Concurrent Read Concurrent Write (CRCW)
    • Smí se paralelně číst a zapisovat
    • Priority-CRCW
      • Zápis povolen pouze procesoru s nejvyšší prioritou
    • Arbitrary-CRCW
      • Zápis povolen náhodně vybranému procesoru
    • Common-CRCW
      • Zápis povolen všem procesorům současně ale všichni musí zapisovat tu samou informaci

APRAM

• Jedná se o výpočetní model Asynchronous Paralel Random Access Machine APRAM
• Procesory pracují asynchronně, neexistují centrální hodiny.
• Operace READ, WRITE, LOCAL jako PRAM.
• Doba přístupu do sdílení paměti není jednotková.
• APRAM výpočet = posloupnost globálních fází, ve kterých procesory pracují asynchronně, oddělených bariérovou synchronizací.
• Explicitní synchronizace: bariérová synchronizace pred přístupem do sdílené paměti
• Implementace bariery:
  • Centrální čítač
    • Složitost: $B(p) = \Theta(dp)$
    • Algoritmus
      1. Centrální čítač se inicializuje na 0 při startu příchozí fáze
      2. Proces dorazí k bariéře, zkontroluje, zda je v příchozí fázi a inkrementuje čítač
      3. Je-li čítač < p, proces se deaktivuje
      4. Jinak nastaví bariéru do odchozí fáze a aktivuje ostatní procesy
      5. Poslední aktivovaný proces nastaví bariéru do příchozí fáze
  • Binární redukční strom
    • Složitost: $B(p) = \Theta(d \log p)$
    • Algoritmus
      1. Process dorazí k bariéře a zkontroluje, zda je v příchozí fázi a zařadí se do stromu
      2. Čeká, až skončí redukce v jeho podstromu
      3. Po jejím skončení pošle signál rodiči
      4. Kořen stromu počká na redukci z obou podstromů a přepne do odchozí fáze
      5. Procesy se aktivují ve zpětném pořadí

Škálovatelnost

• Škálovatelnost: Schopnost paralelního algoritmu držet paralelní optimalitu
• Silná škálovatelnost
  • Měří schopnost paralelního algoritmu pro fixní $n$ dosáhnout lineárního zrychlení s rostoucím $p$
  • Měřítko rychlosti poklesu efektivnosti při rostoucím $p$ a konstantním $n$
• Slabá škálovatelnost
  • Sleduje změnu paralelního času s $p$ pro fixní $n/p$
  • Měřítko růstu $n$ takového, že při rostoucím $p$ zůstává efektivnost konstantní

Amdahlův zákon

• Nezávisle na tom, kolik vláken je spuštěno tak, zrychlení nemůže přesáhnout $\frac{1}{f_s}$
• Mluví o tom ze každý sekvenční algoritmus se skládá z paralelizovatelné části a inherentně sekvenci části a paralelní algoritmus ma omezené zrychleni sekvenční částí
  • inherentně sekvenci část: $f_s$
  • paralelizovatelná část: $1-f_s$
• $$S(n,p)=\frac{T_A(n)}{f_s\cdot T_A(n) + \frac{1-f_s}{p}\cdot T_A(n)}=\frac{1}{f_s+\frac{1-f_s}{p}}\leq \frac{1}{f_s}$$

Gustafsonův zákon

• Gustafsonův zákon říká, že s rostoucím počtem procesorů $p$ máme úměrně navyšovat i velikost problému $n$.
• Zvětšování problému kompenzujeme omezení sekvenčních částí
• $$S(n,p) = \frac{t_{seq} + t_{par}(n,1)}{t_{seq} + t_{par}(n,p)}$$

Izoefektivní funkce

• Izoefektivní funkce ψ1(p)
  • Jak velký problém musím mít, aby mi algoritmus zůstal efektivní při daném počtu procesorů?
  • Pro konstantu $0 < E_0 < 1$ je $\psi_1(p)$ asymptoticky minimální funkce taková, že:

$$\forall n_p = \Omega(\psi_1(p)) : E(n_p, p) \geq E_0$$

• Izoefektivní funkce ψ2(n)
  • Kolik procesorů můžu maximálně použít, aby mi algoritmus zůstal efektivní pro danou velikost problému?
  • Pro konstantu $0 < E_0 < 1$ je $\psi_2(n)$ asymptoticky maximální funkce taková, že:

$$\forall p_n = O(\psi_2(n)) : E(n, p_n) \geq E_0$$

• $E_0$ reprezentuje fixní efektivitu
• $\psi_1(p)$ udává minimální velikost problému pro daný počet procesorů
• $\psi_2(n)$ udává maximální počet procesorů pro danou velikost problému
• Obě funkce garantují minimální efektivitu $E_0$