17. Programování nad sdílenou pamětí, programový model OpenMP, datový a funkční paralelismus, synchronizace vláken, vícevláknové algoritmy (násobení polynomů, násobení matic a vektorů, řazení). (NI-PDP)¶

OpenMP¶

High level API pro sdíleně-paměťové paralelní programování
OpenMP je explicitní model paralelního výpočtu, kdy programátor ma plnou kontrolu a zodpovědnost za paralelní výpočet.
OpenMP funguje se sdílenou pamětí
Program začne vždy s počátečním vláknem pokud se kód dostane do paralelního regionu vytvoří tam skupinu paralelně běžících vláken pomoci fork-join mechanismu
Na konci paralelního regionu je implicitní bariéra

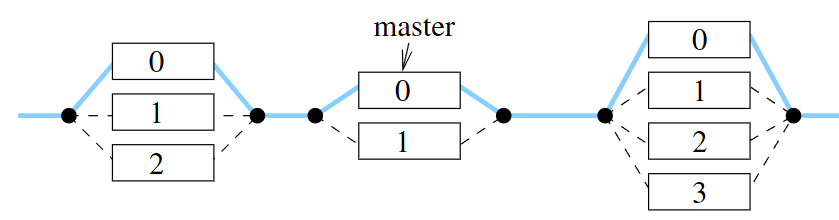
Pasted image 20250122180443.png

Mimo paralelní oblasti běží počáteční vlákno sekvenčně
OpenMP může využívat thread pool pro recyklaci vláken
Změna v sdílené paměti se nemusí hned zpropagovat k ostatním vláknům.
- Pro explicitní synchronizaci se využívá flush
Neefektivita
- Falešné sdílení – různá vlákna zapisují na různé adresy, které jsou ale natolik blízké, že jsou namapovány do stejného bloku keš paměti
- Nevyvážená výpočetní zátěž pro jednotlivá vlákna – bariéra → čekající vlákna → nevyužitá jádra
- Příliš těsná synchronizace – velký počet bariér/krit. sekcí
- Omezený paralelismus – # iterací for < # vláken
- Vysoká režie správy vláken – častá tvorba/zánik, schedule(dynamic)
- Významná sekvenční část – z Amdahlova zákonu

Datový parallelismus¶

Každé vlákno vykonává stejnou operaci, ale nad různými daty
Data rozdělíme mezi procesory/vlákna pomoci schedule
Vhodné pro pole, matice, hromadné výpočty
V OpenMP pomocí #pragma omp parallel for
Řízení paralelismu Schedule - Určuje, jakým způsobem se rozděluje práce mezi vlákna
- static - Práce je rozdělena po blocích
- dynamic - Práce je rozdělena v průběhu zpracovaní
- guided - Práce je rozdělena do prvotních bloku. Bloky se postupně zmenšují v průběhu zpracovaní
Pro vnořené cykly využijeme klauzuli collapse
Pro parallelismus vnitřního for loop vytvoříme paralelní region okolo vnějšího for a pro vnitřní for zahájíme parallelismus

Funkční parallelismus¶

Paralelizujeme různé úlohy, které mohou vykonávat různé operace
Mezi vlákna tedy nerozdělujeme kusy dat, ale jednotlivá volání funkcí
Vhodné pro rekurzivní algoritmy
V OpenMP pomocí #pragma omp task
Zahájeni task musí byt uvnitř paralelního regionu
single umožní zahájení procesu. Zavolá funkci pouze jednou
Pro rekurzivní algoritmy si musíme dat pozor abychom balancovali paralelní větvení a sekvenční řešení

Synchronizace vláken¶

V OpenMP řešení synchronizace a datových závislostí je ponecháno na programátorovi
Nástroje OpenMP
- Kritická sekce
  - K dane části kódu paralelní oblasti může přistupovat pouze jedno vlákno v jednu chvíli, ostatní čekají, až bude volno
  - Stejně pojmenované kritické sekce funguji jako jedna kritická sekce
- Atomické operace
  - Kritická sekce pro jednu proměnou. Zajisti ze operace proběhne atomicky.
  - Možné aplikace: read, write, update, capture
  - Ma menší overhead než kritická sekce
  - Musi existovat hardware podpora
- Barrier
  - Synchronizační segment u kterého se ceká dokud k němu nedorazí všechna vlákna
- Master
  - Danou cast kódu provede pouze hlavni vlákno
- Single
  - Danou cast kódu provede pouze jedno vlákno
- Cancel
  - Direktiva která bezpečně ale předčasně ukončí paralelní výpočet

Vícevláknové algoritmy¶

Násobení polynomů¶

Máme polynomy $A=\sum_{i=0}^n a_ix^i,\quad B=\sum_{j=0}^n b_jx^j$
Chceme $C = A \times B = \sum_i^n\sum_j^m (a_i*b_j)x^{i+j}$

Sekvenci řešení¶

int A[m+1],B[n+1] // Input polynoms
int C[n+m+1] = 0; // Init C to all zero

for (int i = 0; i <= m; i++)
    for (int j = 0; j <= n; j++)
        C[i+j] += A[i]*B[j];

Paralelní řešení¶

Typy paralelizace
- Vnější cyklus
  - Vytvoříme datový parallelismus na vnější cyklus
  - Vyžaduje atomic update na násobení $a_j$ a $b_j$
- Vnitřní cyklus
  - Vytvoříme datový parallelismus na vnitřní cyklus
  - Nevyžaduje atomic update na násobení $a_j$ a $b_j$
- Paralelizace založená na dekompozici výstupního polynomu na disjunktní oblasti zápis· podle hodnoty součtu $i + j$ .
  - Vytvoříme datový parallelismus na vnější cyklus
  - Vnitřní for loop uděláme tak aby sčítal pouze ty polynomy které v součtu mocnin dávají výsledek roven iteraci vnějšího cyklu

Paralelizace vnitřním cyklem

int A[m+1], B[n+1], C[n+m+1]; //parallel inner loop
#pragma omp parallel
for (int i = 0; i <= m; i++) //in each iter. p new threads are forked
    #pragma omp for schedule(static)
    for (int j = 0; j <= n; j++) //parallel Reads of the same A[i]
        C[i+j] += A[i]*B[j]; //disjoint Reads of B and Writes of C

Paralelizace dekompozicí

#pragma omp parallel for schedule(static)
for (int k = 0; k <= (m + n); y++)
    for (int l = max(0, k - n); l <= min(k,m); l++)
        C[k] += A[l]*B[k-l];

Násobení matic¶

Mějme dvě čtvercové matice $A,\ B$ o rozměrech $n\times n$
Cílem je vypočítat $C = A\times B$

Sekvenční řešení¶

float A[n][n], B[n][n], C[n][n];
for (int i = 0; i < n; i++) // Row loop
    for (int j = 0; j < n; j++) { //Column loop
        float s = 0.0;
        for (int k = 0; k < n; k++) //Scalar product loop
            s += A[i][k]*B[k][j];
        C[i][j] = s; 
    }

Paralelní řešení¶

Typy paralelizace
- Paralelizace přes řádky
  - Vytvoříme datový parallelismus na první (vnější) cyklus
  - Minimální synchronizace
  - 1 bariera na konci
- Paralelizace přes sloupce
  - Vytvoříme datový parallelismus na druhy cyklus
  - Vetší synchronizace
  - $n/p$ barier
- Paralelizace přes skalární součet
  - Vytvoříme datový parallelismus na třetí (vnitřní) cyklus
  - Největší synchronizace

Násobení řídké matice vektorem¶

Mějme řídkou čtvercovou matici $A$ o rozměrech $n\times n$ a vektor $x$ velikosti $n$
Cílem je vypočítat $y = xA$
Počet nenulových prvku v matici $A$ je $N$

Souřadnicový formát¶

Souřadnicový formát (COOrdinate Format - COO) je jednoduchá reprezentace řídkých matic
Máme 3 pole
- Indexy Radku
- Indexy sloupců
- Hodnoty buněk
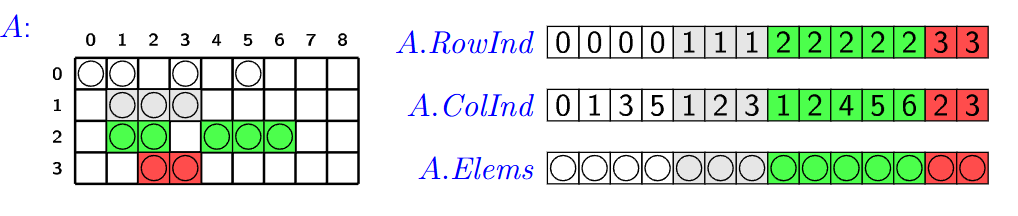
Máme jeden for loop na který můžeme použít datový paralelismus
- Vyžaduje atomic update při násobeni

struct A; float x[n]; float y[n];
#pragma omp parallel for
for (int i = 0; i < n; i++)
    y[i] = 0.0; //initialization of vector y
#pragma omp parallel for
for (int k = 0; k < N; k++) {
    float temp = A.Elems[k] * x[A.ColInd[k]];
    #pragma omp atomic update
    y[A.RowInd[k]] += temp;
}

Komprimovaný souřadnicový formát¶

Komprimovaný souřadnicový formát (Compressed Sparse Row - CSR) je reprezentace řídkých matic podobna COO až na to že řádky jsou znázorněny implicitně
Máme 3 pole
- Indexy do pole sloupců
- Indexy sloupců
- Hodnoty buněk
Máme 2 for loop jeden jde přes indexy sloupců a druhy přes samotné sloupce
- Při paralelizaci přes vnější cyklus nebudou nastávat kolize použijeme tedy to.

struct A; //sparse matrix in the CSR format
float x[n]; //array representing the input vector x
float y[n]; //array representing the output vector y=Ax
#pragma omp parallel for schedule([static[,X]]|[dynamic[,X]])
for (i = 0; i < n; i++) { //loop on rows
    sum = 0.0;
    for (k = A.RowStart[i]; k < A.RowStart[i+1]; k++) {
        //iterate over nonzero elements of one row
        sum += A.Elems[k] * x[A.ColInd[k]];
    }
    y[i] = sum;
}

QuickSort¶

QuickSort je algoritmus řazení s průměrnou časovou složitostí $O(n\cdot log(n))$ . Funguje tak, že vybere 'pivot' prvek a rozdělí pole na dvě podpole, takže prvky menší než pivot jsou před ním a prvky větší než pivot za ním. Tato podpole jsou pak rekurzivně seřazena.

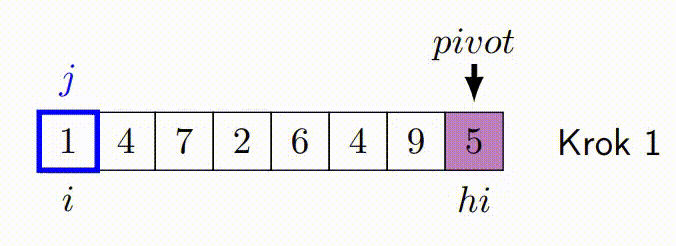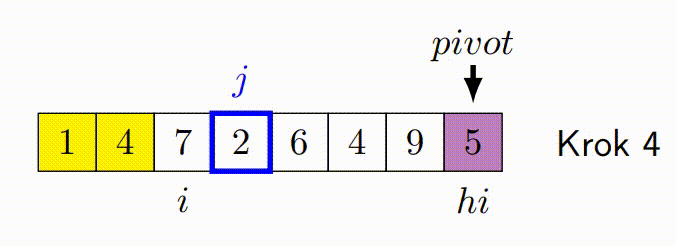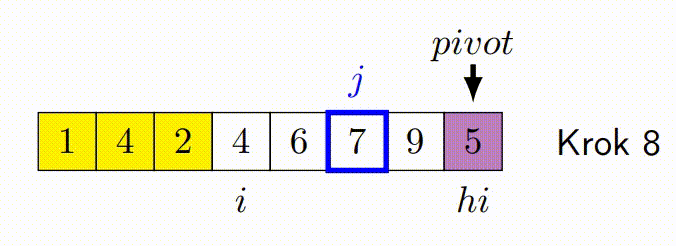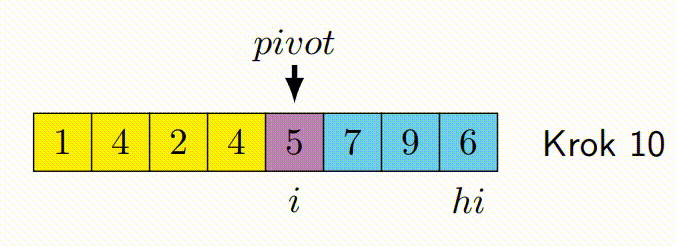
Recording 2023-06-20 180043.gif

Základní Paralelizace Pomocí Úloh¶

Základní myšlenka paralelizace QuickSortu spočívá v provádění rekurzivních volání na levé a pravé části paralelně.
Toho lze dosáhnout pomocí OpenMP direktivy #pragma omp task pro levou a pravou část.
Prah počtu úloh: Použijte direktivu #pragma omp task if(depth < DEPTH_THRESHOLD) k nastavení prahu pro hloubku rekurze, do které by měly být vytvářeny úlohy.
Nahrazení jednoho z rekurzivních volání iterací: Tímto lze snížit počet vytvořených úloh na polovinu.
Vyvažování Zátěže: Rozdělte vlákna mezi levé a pravé části podle jejich velikosti.
Paralelní Rozdělení: Kromě paralelního řazení také paralelizujte fázi rozdělení.

const int DEPTH_THRESHOLD = 4;

void parallel_quicksort(int* arr, long low, long high) {
    #pragma omp parallel // Create a team of threads
    {
        #pragma omp single // Only a single thread executes the recursive calls
            par_quicksort_rec(arr, low, high, 0);
    }
}

void par_quicksort_rec(int* arr, long low, long high, int depth) {
    while (low < high) {
        long pivotIndex = partition(arr, low, high); 

        #pragma omp task if (depth < DEPTH_THRESHOLD) // Limit the depth of recursion for task creation
        par_quicksort_rec(arr, low, pivotIndex - 1, depth + 1);

        // Using iteration instead of recursion for the right part
        depth += 1
        low = pivotIndex + 1;
    }
}

Hoareuv QuickSort¶

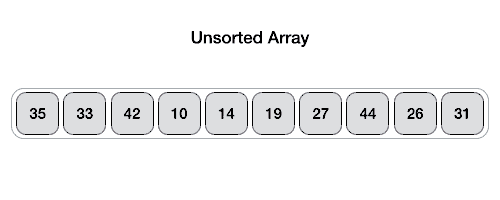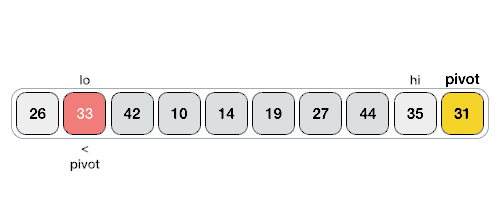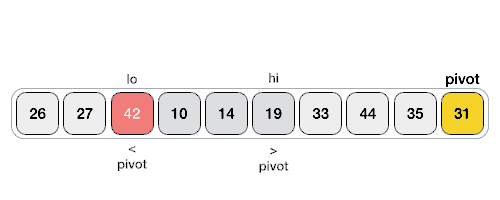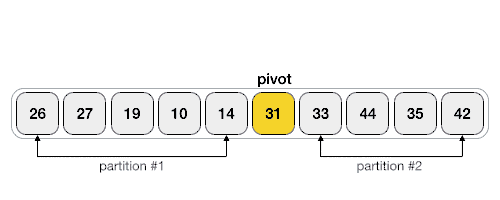
Vybere pivotní prvek, často první nebo poslední prvek v podpoli.
Má dva ukazatele - jeden na začátku pole a druhý na konci.
Ukazatele se pohybují proti sobě. Levý ukazatel postupuje doprava, dokud nenajde prvek větší než pivot. Pravý ukazatel postupuje doleva, dokud nenajde prvek menší než pivot.
Pokud se ukazatele ještě nepřekřížily, prohodí nalezené prvky a pokračují v krocích 3 a 4.
Proces končí, když se ukazatele překříží. Pole je pak rozděleno na dva segmenty, prvky menší než pivot a prvky větší než pivot.

hoaer quick sort.gif

Hoareho Paralelní Algoritmus Rozdělení¶

Máme dva ukazatele, které se pohybují proti sobě.
Pozice těchto ukazatelů lze upravit pomocí #pragma omp atomic capture.
Na konci mohou zůstat „špinavá čísla“ (prvky v nesprávné části), která je potřeba přehodit sekvenčně.
Maximálně můžu získat $p$ špinavých bloků, tedy tolik špinavých bloků, kolik je počet vláken.
Nakonec projedu pole sekvenčně, abych opravil špinavé bloky.
Nevyhody:
- Vysoký Počet Synchronizačních Operací
- False sharing
- Vyvažování Zátěže

hoare paralel bad.gif

Vylepšený Paralelní Algoritmus Rozdělení v Hoareově QuickSortu¶

Vylepšený paralelní algoritmus rozdělení v Hoareově QuickSortu se zaměřuje na efektivní paralelizaci fáze rozdělení. Tato fáze je kritická, protože určuje, jak se prvky rozdělí kolem vybraného pivotu. Vylepšená verze se snaží minimalizovat počet špinavých bloků a maximalizovat efektivitu paralelního zpracování.

Následující kroky popisují, jak vylepšený paralelní algoritmus rozdělení funguje:

Inicializace: V algoritmu se vybere pivot, podobně jako v klasickém Hoareově algoritmu. Algoritmus také inicializuje ukazatele, které budou procházet polem od obou konců. Na rozdíl od klasického přístupu, vylepšená verze rozdělí data do bloků, které budou zpracovávány paralelně.
Paralelní Zpracování Bloků: Každé vlákno zpracovává blok prvků a porovnává je s pivotem. Podle porovnání zařadí prvky za sebe, tj. prvky menší než pivot umisťuje na jednu stranu a prvky větší než pivot na druhou stranu ve svém bloku. Důležité je, že každý blok je zpracováván sekvenčně a nejsou zde použity žádné zámky, což minimalizuje režii synchronizace.
Pohyb Ukazatelů a Kontinuální Zpracování Bloků: Základní myšlenka s ukazateli zůstává stejná jako v klasickém Hoareově algoritmu, ale místo přepínání vláken po každém prvku se ukazatele pohybují po zpracovaných blocích. Pokud je zpracován levý blok, ukazatel vezme další levý blok a pokračuje v jeho zpracování zatimco pravy blok pokracuje tam kde zkoncil. Tento princip platí i naopak pro pravý ukazatel. Tato technika snižuje počet nutných synchronizačních operací mezi vlákny a zlepšuje výkon.
Oprava Špinavých Bloků: Po dokončení paralelního kroku mohou existovat $p$ špinavých bloků, což jsou bloky, které obsahují prvky, které ještě nebyly správně rozděleny (některé by mohly být menší a jiné větší než pivot). Tento krok spočívá v sekvenčním seřazení těchto špinavých bloků, aby bylo zajištěno, že pole je správně rozděleno kolem pivotu.

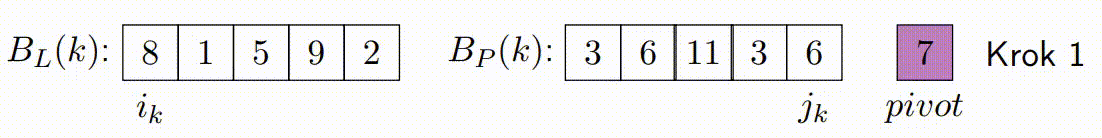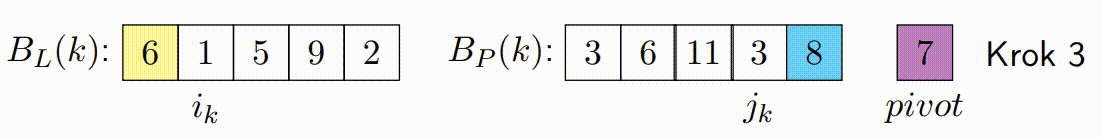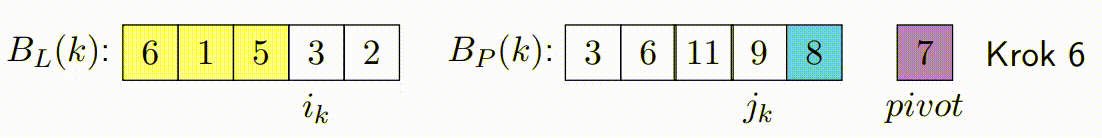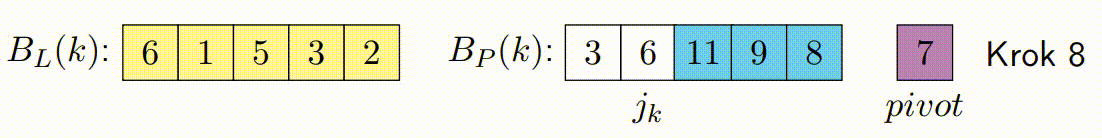
hoare paralel good.gif

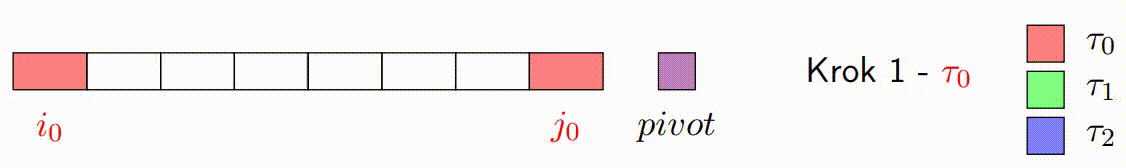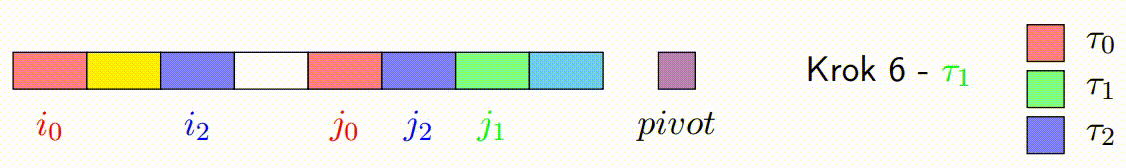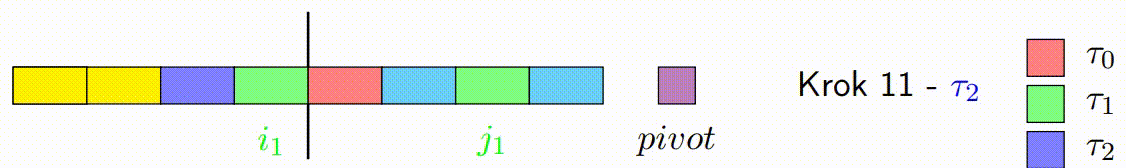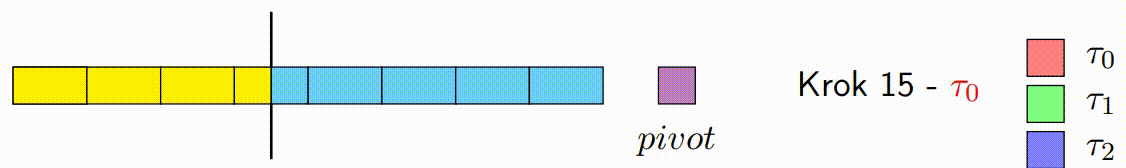
hoare paralel good overview.gif

const long K = ...; // Definujte hodnotu K

long par_partition_block(int* A, long lo, long hi) {
    long pivot = A[hi];
    long i = lo;
    long j = hi - 1;

    #pragma omp parallel
    {
        long my_i, my_j, init_my_i, init_my_j;

        #pragma omp atomic capture
        {
            my_i = i;
            i += K;
        }

        #pragma omp atomic capture
        {
            my_j = j;
            j -= K;
        }

        init_my_i = my_i;
        init_my_j = my_j;

        while (my_i < my_j) {
            // Předpokládám, že funkce 'neutralizace' je někde definována
            neutralizace(A, my_i, init_my_i, my_j, init_my_j, K, pivot);

            if (my_i >= init_my_i + K) {
                #pragma omp atomic capture
                {
                    my_i = i;
                    i += K;
                }
                init_my_i = my_i;
            }

            if (my_j <= init_my_j - K) {
                #pragma omp atomic capture
                {
                    my_j = j;
                    j -= K;
                }
                init_my_j = my_j;
            }
        }

        #pragma omp barrier

        // ...neutralizace max. p zbývajících bloků
    }

    // ...úklid posledního špinavého bloku

    return j; //vrácení indexu hranice mezi levým a pravým segmentem
}

MergeSort¶

Merge Sort, neboli algoritmus řazení sléváním, je jeden z klasických algoritmů pro řazení dat. Merge sort pracuje na principu "rozlož a panuj".

Nejprve rekurzivně rozděluje pole až na jednotlivé prvky, poté postupně slučuje sousední podpole, přičemž je seřazuje. Tento proces pokračuje, dokud nejsou všechna podpole spojena do jednoho seřazeného celku.

Základní Princip:

Rozdělení pole na dvě menší podčásti
Seřazení těchto podčástí
Sloučení těchto dvou seřazených polí do jednoho seřazeného pole

Základní Task Paralelizace¶

Zde využijeme OpenMP k vytvoření úloh (tasks) pro levou a pravou část pole.
Prah počtu úloh: Použití podmínky pro omezení hloubky rekurze.
Snížení počtu úloh: Nahrazení jednoho rekurzivního volání iterací. To snižuje počet úloh na polovinu.
Paralelizace slučovací operace: Kromě paralelního řazení je také možné paralelizovat slučovací operaci. To zrychluje celkový proces.

Paralelní Dvoucestné Slučování¶

Paralelní dvoucestné slučování je technika optimalizace slučovací fáze Merge Sort algoritmu, když pracujeme s více procesorovými vlákny.

Krok 1: Vytvoření Matice Přechodů¶

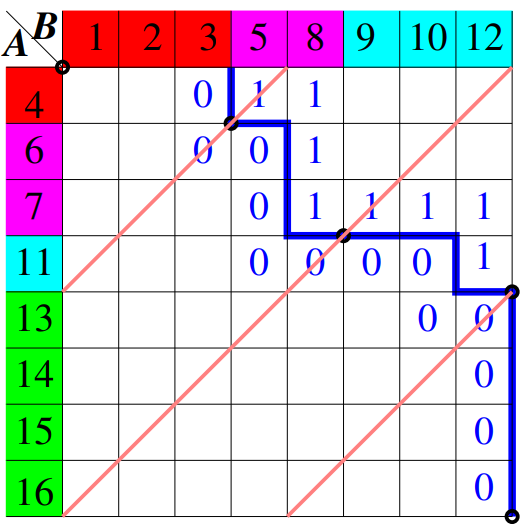
Máme dvě seřazená pole, A a B. Naším cílem je sloučit tato dvě pole do jednoho seřazeného pole C. Nejprve si sekvenčně vytvoříme matici X, kde každý prvek $X[i][j]$ je 0, pokud $A[i] > B[j]$ , a 1 v opačném případě. Protože pole jsou seřazená, bude existovat přechod mezi hodnotami 0 a 1 v této matici.

Krok 2: Diagonální Proložení¶

Nyní chceme rozdělit práci mezi více vlákny. K tomu použijeme techniku nazývanou diagonální proložení. Proložíme matici X s $(p-1)$ vedlejšími diagonálami, kde $p$ je počet vláken, které chceme použít. Tyto diagonály jsou ekvidistantní a rozdělují matici do bloků.

Krok 3: Výpočet Průsečíků¶

Pro každou diagonálu potřebujeme najít průsečík s přechodem mezi hodnotami 0 a 1 v matici. To nám pomůže určit, jaká část pole A a B by měla být sloučena daným vláknem. Průsečíky lze najít pomocí binárního půlení

Pasted image 20230616124452.png

Krok 4: Sloučení Bloků¶

Nyní každé vlákno provede slučovací operaci sekvenčně na svých přidělených blocích. To znamená, že vlákno $i$ sloučí bloky $A_i$ a $B_i$ na základě vypočtených průsečíků.

Krok 5: Spojení Výsledků¶

Na konci, po dokončení slučovací operace ve všech vláknech, spojíme výsledné bloky od všech vláken k vytvoření finálního seřazeného pole C.

Paralelní p-cestný MergeSort¶

Krok 1: Rozdělení dat na podčásti¶

Příprava: Máme vstupní pole $S$ o velikosti $n$ a chceme ho rozdělit na $p$ podpolí, kde $p$ je počet dostupných vláken. Každé podpole bude mít velikost přibližně $n/p$ .
Rozdělení: To znamená, že rozdělíme pole $S$ na menší podpolí $S[0], S[1], ..., S[p-1]$ .

Krok 2: Seřazení podčástí¶

Paralelní seřazení: Každé vlákno je zodpovědné za seřazení jednoho z podpolí. To znamená, že vlákno $i$ bude seřazovat podpole $S[i]$ .
Potom následuje bariera.

Krok 3: Výpočet oddělovačů¶

Určení oddělovačů: Po seřazení pod částí potřebujeme určit oddělovače. Každé vlákno potřebuje najit takový oddělovač který když aplikuje na seřazené pod časti tak ten pivot bude oddělovat čísla tak aby pred pivotem bylo $\text{id} * (n/p)$ čísel.
Význam oddělovačů: Oddělovače nám pomohou určit, jaké části různých podpolí se mají sloučit do jednoho kontinuálního seřazeného segmentu.

Krok 4: Sloučení úseků¶

Paralelní sloučení: Vlákna nyní začnou slučovat části, které jim byly přiděleny na základě oddělovačů. To je provedeno tak, že každé vlákno sloučí své příslušné úseky do jednoho kontinuálního seřazeného segmentu .
Slučovací algoritmus: Slučování může být provedeno pomocí standardního sekvenčního slučovacího algoritmu, který spojuje p seřazených seznamu do jednoho seřazeného seznamu.

Pasted image 20230616125305.png

Krok 5: Konečná synchronizace¶

Po dokončení slučovacích operací všech vláken, budeme mít $p$ seřazených segmentů. Tyto segmenty potom můžeme ještě jednou sloučit do jednoho výsledného seřazeného pole.
Je důležité zajistit, že vlákna jsou synchronizovaná před tímto krokem, aby se zabránilo jakýmkoli problémům s přístupem k datům.