18. Programování nad distribuovanou pamětí, programový model MPI (vícevláknové procesy, komunikátory, 2-bodové blokující a neblokující komunikační operace, kolektivní operace), paralelní násobení hustých matic, paralelní mocninná metoda. (NI-PDP)

---

MPI

• MPI (Message Passing Interface) je standard pro komunikaci mezi procesy, který umožňuje efektivní distribuované programování napříč více stroji.
• Veškeré proměnné jsou privátní, každý MPI proces má svoje instance.
• Paměť není sdílená

Vícevláknové procesy

• Model kombinace MPI a OpenMP: Na každém výpočetním uzlu/procesoru běží jeden nebo několik málo MPI proces, a ty se pomocí OpenMP dělí na několik vláken, běžících na jádrech.
  • V rámci jednoho uzlu se pomoci OpenMP může využít sdílena paměť, a tedy zrychlit komunikaci mezi vlákny
  • Pro počítače s vice CPU je vhodné využít MPI pro každé CPU a OpenMP v rámci jednoho CPU
• Pro kombinaci MPI a OpenMP existují tyto módy:
  • MPI_THREAD_SINGLE = program nesmí být vícevláknový
  • MPI_THREAD_FUNNELED = MPI lze volat jen z hlavního vlákna
  • MPI_THREAD_SERIALIZED = MPI lze volat v jednom okamžiku jen z jednoho vlákna
  • MPI_THREAD_MULTIPLE = MPI lze volat z více vláken bez omezení
• Podpora těchto módů záleží na implementaci MPI

Komunikátory

• Každá komunikační MPI funkce má jako parametr tzv. komunikátor.
• Komunikátor určuje množinu procesů, v rámci níž probíhá komunikace.
• Typy:
  • Intra-komunikátor je asociovaný s konkrétní skupinou procesů a určuje komunikaci mezi procesy uvnitř této skupiny.
  • MPI_COMM_WORLD je implicitní předdefinovaný intra-komunikátor pro skupinu všech procesů MPI programu.
  • Inter-komunikátor je asociovaný s dvěma různými skupinami procesů a určuje komunikaci mezi procesy z těchto skupin (nebude dále rozváděno).
• MPI_Comm_rank: Zjištění číslo procesu
• MPI_Comm_size: Zjištění počet procesu

Komunikační operace

Kazda komunikační operace obsahuje:

• buffer - Odkud brat data k poslaní / Kam dat data pro odeslaní
• count - Počet posílaných položek
• datatype
• source/destination - Číslo procesu; Skupiny procesu; Všech procesu (Bez omezeni)
• komunikátor

Taxonomie

1. 2-bodové (Point-to-point): Komunikace mezi dvěma MPI procesy.
2. Kolektivní (Collective): Komunikace mezi všemi procesy asociovanými s daným komunikátorem.

Blokující vs. Neblokující Komunikační Operace

• Blokující operace: MPI funkce se dokončí až po té co lze modifikovat vstupní buffer.
  • Lokalita - Lokální komunikace nepotřebuje data o příjemci nelokální potřebuje
  • Mody: Funkce se dokončí až:
    • Standartní: Se zprava odešle danému procesu nebo se překopíruje do systémového bufferu (Nelokální / Lokální operace)
    • Buffered: Se zprava překopíruje do systémového bufferu (Lokální operace)
    • Synchronní: Se zahájí komunikace mezi procesy a přijme se zprava (Nelokální operace)
    • Ready: Se zahájí komunikace mezi procesy, pokud není příjemce ready vrátí se chyba (Nelokální operace)
• Neblokující operace: MPI funkce se dokončí okamžitě a stav komunikace musí být následně testován.
  • Probe: Počká než přijde zprava. Nepřijme ji
  • IProbe: Testuje zda správa přišla. Nepřijme ji

Kolektivní operace

• Operace prováděné nad vsemi procesy
• Existuji blokující i neblokující verze
• Typy Jeden-Mnoha:
  • One-To-All Broadcast: Rozeslání dat z jednoho procesu všem ostatním
  • One-To-All Scatter: Rozdělení dat z jednoho procesu mezi všechny procesy
  • All-To-One: Shromáždění dat ze všech procesů do jednoho
  • Multicast: Odeslání dat podmnožině procesů
• Typy Všichni - Všem
  • All-to-All Broadcast: Každý proces rozešle svá data všem ostatním
  • All-to-All Gather: Každý proces shromáždí data ze všech procesů
  • All-to-All Scatter: Každý proces rozešle část svých dat všem ostatním procesům

Násobení hustých matic

• Máme dvě husté čtvercové matice $A \in \mathbb{R}^{n \times n}$ a $B \in \mathbb{R}^{n \times n}$ o rozměrech $n \times n$, a
• Cil je získat matici: $C = A\times B$.

Cannonův algoritmus

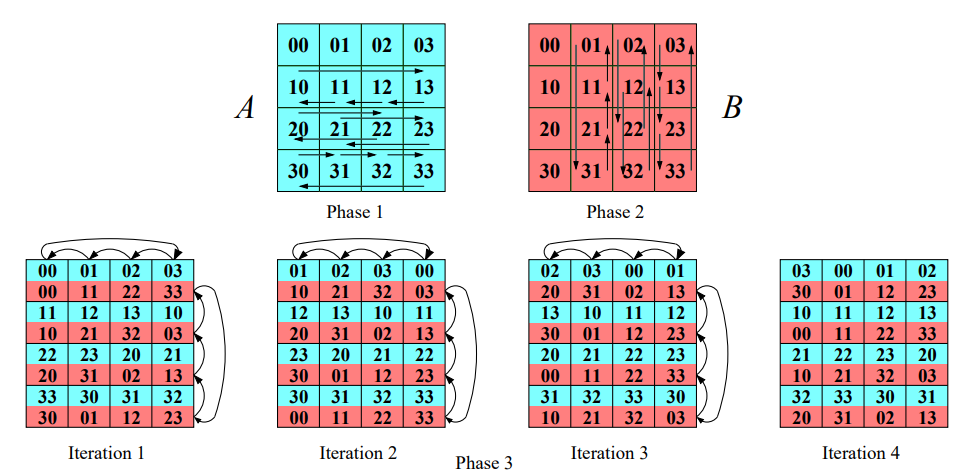
• Cannonův algoritmus je založen na dělení matic na menší podmatice a provádění operací na těchto podmaticích paralelně.
• V tomto algoritmu je důležitá struktura komunikační sítě, kterou představuje 2D torus.
• Předpokládejme, že máme $p$ vláken a každé vlákno pracuje s maticí o rozměru $\sqrt{p} \times \sqrt{p}$.
• V případě $p$ procesoru každý procesor bude násobit $C_{i,k} = \sum_{j=0}^{\sqrt{p}-1}A_{i,j}B_{j,k}$

Kroky algoritmu

1. Inicializace: V první fázi posuneme řádky matice $A$ o $i$ pozic doleva a sloupce matice $B$ o $i$ pozic nahoru, kde $i$ je index řádku resp. sloupce a $i \in {0, \dots, p-1}$.

2. Násobení a rotace podmatic: Nyní provedeme násobení jednotlivých podmatic lokálně. Po provedení násobení rotujeme každý řádek matice $A$ o jednu pozici doleva a každý sloupec matice $B$ o jednu pozici nahoru. Tyto kroky se opakují $p$-krát.

3. Sčítání výsledků: Každé vlákno sečte své výsledky do výsledné matice $C$.

Algorithm CannonMMM(A, B; C)
    // F1: Inicializační rotace řádků matice A
    for all i = 0 to √p - 1 do_in_parallel
        rotate submatrices A_{i,*} in row i left by i positions

    // F2: Inicializační rotace sloupců matice B
    for all k = 0 to √p - 1 do_in_parallel
        rotate submatrices B_{*,k} in column k up by k positions

    // F3: Hlavní výpočetní smyčka
    repeat √p times
    {
        // Paralelní násobení submatic
        for all i, k = 0 to √p - 1 do_in_parallel
            P_{i,k} multiply current submatrices A and B and add result to C_{i,k}

        // Rotace řádků matice A
        for all i = 0 to √p - 1 do_in_parallel
            rotate submatrices A_{i,*} in row i left by 1 position

        // Rotace sloupců matice B
        for all k = 0 to √p - 1 do_in_parallel
            rotate submatrices B_{*,k} in column k up by 1 position
    }

Foxuv algoritmus

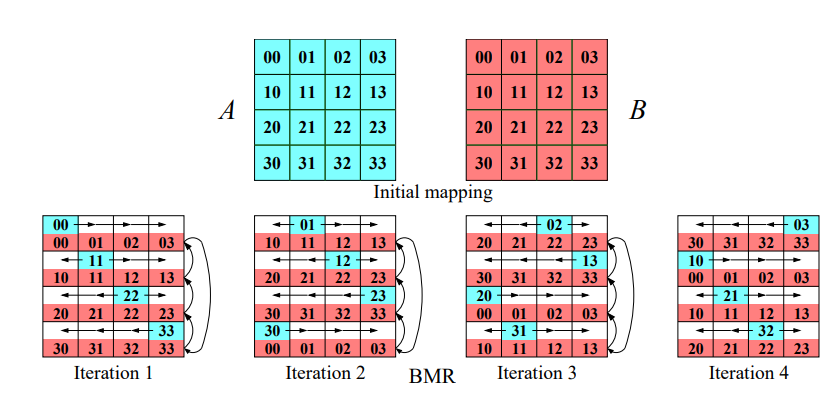
• Foxův algoritmus je alternativní metodou k Cannonovu algoritmu, avšak s jiným způsobem komunikace mezi procesory.
• Opět využívá strukturu komunikační sítě 2D torus a pracuje s $p$ vlákny, kde každé vlákno pracuje s maticí o rozměru $\sqrt{p} \times \sqrt{p}$.

Kroky algoritmu

1. Broadcast matice $A$: V prvním kroku algoritmus provádí broadcast řádků matice $A$, začínajíc u hlavní diagonály.

2. Násobení a rotace podmatic: Vlákna následně vynásobí podmatice lokálně a rotují každý sloupec matice $B$ o jednu pozici nahoru. Tyto kroky se opakují $p$-krát.

3. Sčítání výsledků: Každé vlákno sečte své výsledky do výsledné matice $C$.

Implementace v MPI

Níže jsou uvedeny kroky pro implementaci Cannonova nebo Foxova algoritmu pomocí MPI.

1. Vytvoření virtuální topologie: V MPI vytvoříme kartézskou topologii, která umožňuje procesorům komunikovat v mřížce.

2. Zjištění souřadnic procesoru: Každý procesor zjistí své souřadnice v kartézské síti.

3. Nastavení kartézského posunu: Pro rotaci matice nastavíme posun (shift) v kartézské topologii.

4. Rotace a komunikace: Provedeme rotaci podmatic pomocí funkce MPI_Cart_shift a vyměníme data mezi procesory pomocí funkce MPI_SendRecv_replace.

5. Lokální násobení a sčítání: Každý procesor vynásobí své podmatice a přičte je do své části výsledné matice.

Paralelní mocninná metoda

Mocninná metoda je iterativní algoritmus, jehož účelem je aproximace dominantního vlastního čísla matice. Má za cíl nalezení největšího vlastního čísla matice $A$ opakovaným násobením matice vektorem $\vec{x}$, tedy $y = A\vec{x}$.

Algoritmus

1. Inicializace: Vyberte libovolný nenulový počáteční vektor $\vec{x}$.

2. Matice-Vektor Násobení (MVM): Vypočítejte $\vec{y} = A\vec{x}$.

3. Normalizace: Spočítejte normu $\alpha$ vektoru $\vec{y}$: $$\alpha \leftarrow \|\vec{y}\|_2 = \sqrt{y_1^2 + y_2^2 + \ldots + y_n^2}$$

4. Aktualizace vektoru: Nahraďte vektor $\vec{x}$ normalizovaným vektorem $\vec{y}$: $\vec{x} = \frac{\vec{y}}{\alpha}$.

5. Konvergenční kritérium: Ověřte, zda je splněno konvergenční kritérium.

6. Opakování: Pokud není konvergenční kritérium splněno, vraťte se k kroku 2. V opačném případě algoritmus končí s $\alpha$ jako aproximací dominantního vlastního čísla.

Paralelní implementace

Náhodné mapování

Každý proces potřebuje celý vektor $\vec{x}$ a $\vec{y}$ pro výpočet své části $\vec{y}$. Na konci každé iterace je použita funkce MPI_Allreduce pro synchronizaci vektoru $\vec{x}$ a $\vec{y}$ mezi procesy.

Řádkové mapování

Každý proces potřebuje celý vektor $\vec{x}$ pro výpočet své části $\vec{y}$. Postupujeme následovně:

1. Provede se MPI_Allgather pro shromáždění celého vektoru $\vec{x}$.
2. Každý proces provede lokální výpočet své části $\vec{y}$.
3. Provede se lokální výpočet normalizace.
4. Vektor $\vec{y}$ se vyřeší normalizovaným výsledkem.
5. Ověří se konvergenční podmínka.
6. Pokud není splněna, vrátíme se k bodu 1.

Šachovnicové mapování

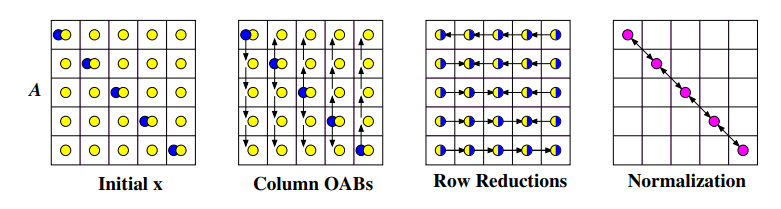
V této strategii každý proces potřebuje pouze svou část vektoru $\vec{x}$.

1. Vektor $\vec{x}$ je namapován na hlavní diagonálu.
2. Procesy na diagonále posílají hodnoty vektoru po sloupcích (sloupcový broadcast).
3. Paralelně všechny procesory spočítají svou část submatice (lokální výpočty).
4. Provede se redukce zpět na diagonálu.
5. Provede se redukce diagonály.
6. Ověří se konvergenční podmínka.
7. Pokud není splněna, vrátíme se k bodu 2.

Implementace v MPI

• Vytvoříme nové komunikační skupiny pro řádky, sloupce a diagonálu.
• Pomocí MPI_Bcast provedeme sloupcový broadcast.
• Pomocí MPI_Reduce zpětně namapujeme hodnoty $\vec{x}$ na diagonálu.
• Pomocí MPI_AllReduce zjistíme normalizaci přes diagonálu.

Paměťová komplexita

Paměťová složitost na proces	Pole x	Pole y
Libovolné	$n$	$n$
Po řádcích	$n$	$\frac{n}{p}$
Šachovnicové	$\frac{n}{\sqrt{p}}$	$\frac{n}{\sqrt{p}}$