19. Přímé ortogonální a hyperkubické propojovací sítě paralelních počítačů (definice, vlastnosti, vnořování). (NI-PDP)

---

Definice grafu

• Grafy, stupeň uzlu, regularita
  • Množina uzlů (= vrcholů) a hran grafu $G$: $V(G)$, $E(G)$
  • Velikost grafu: $N = |V(G)|$
  • Sousední uzly $u$ a $v$ = hrana $\langle u, v \rangle$
  • Stupeň uzlu $u$: $\deg_G(u) = \#$ počet sousedů uzlu $u$
  • Množina stupňů grafu $G$: $\deg(G) = \{\deg_G(u); u \in V(G)\}$
  • Maximální stupeň grafu $G$: $\Delta(G) = \max(\deg(G))$
  • Minimální stupeň grafu $G$: $\delta(G) = \min(\deg(G))$
  • $k$-regulární graf $G$: $\Delta(G) = \delta(G) = k$

Important

• Bisekční šířka 𝑏𝑤𝑒(𝐺) = velikost nejmenšího hranového řezu grafu na 2 (skoro stejné) poloviny
• Souvislost
  • Uzlový (hranový) rez: množina uzlu (hran), jejichž odebráním se rozpojí graf.
  • Uzlová (hranová) souvislost: Velikost minimálního uzlového (hranového) rezu
• Uzlová symetrie = pro libovolnou dvojici uzlů 𝑢 a 𝑣 existuje atomorfismus, který zobrazí 𝑢 na 𝑣
• Bipartita = existuje obarvení vrcholu dvěma barvami tak, že koncové vrcholy každé hrany mají odlišnou barvu
• Kartézský součin – k. s. množin vrcholů, a hrana vede tehdy, pokud vedla původně v jednom nebo druhém grafu
• Topologie $G_n$:
  • Množina grafů, jejichž velikost a struktura je definována parametrem $n$
  • Hierarchicky rekurzivní topologie: instance menších dimenzí jsou podgrafy instancí větších dimenzí
  • Inkrementálně škálovatelná topologie: definovaná pro $\forall n$
  • Částečně škálovatelná topologie: definovaná pro některá, ale ne všechna $n$
• Hustota topologie:
  • Řídká topologie: $|E(G_n)| = O(|V(G_n)|)$ (stupně uzlů omezeny konstantou)
  • Hustá topologie: $|E(G_n)| = \omega(|V(G_n)|)$ (stupně uzlů rostoucí funkcí $n$)

• Vzdálenosti v grafu:
  • Délka cesty $P(u,v)$: $\text{len}(P(u,v)) =$ počet hran v $P(u,v)$
  • Vzdálenost uzlů $u$ a $v$: $\text{dist}_G(u,v) =$ délka nejkratší cesty $P(u,v)$ v $G$
  • Průměrná vzdálenost v $N$-uzlovém $G$: $\text{dist}(G) = \frac{1}{N(N-1)} \sum_{u \neq v} \text{dist}_G(u,v)$
  • Excentricita uzlu $u$: $\text{exc}(u) = \max_{v \in V(G)} \text{dist}_G(u,v)$
  • Průměr grafu $G$: $\text{diam}(G) = \max_{u,v} \text{dist}_G(u,v) = \max_u \text{exc}(u)$
  • Poloměr grafu $G$: $r(G) = \min_u \text{exc}(u)$

Přímé ortogonální topologie

Important

• Požadavky na topologie
• Konstantní stupeň uzlu x Maly průměr a mala průměrná vzdálenost
  • Požadavky jsou protichůdné
• Uzlová symetrie a hierarchická rekurzivita
• Vysoká souvislost
  • Redundantnost v případě přetržení linek nebo výpadek uzlů
• Velká bisekční sirka
  • Vysoka přenosová kapacita mezi oběma polovinami
  • Mnoho externích spojů mezi stavebními bloky
• Vnořitelnost jiných a do jiných topologií
  • Efektivnost zaleží na efektivním zobrazeni daného grafu do propojovací site
  • Schopnost simulovat efektivně jiné topologie
• Podpora pro směrovaní a kolektivní komunikační operace

n-Rozměrná mřížka

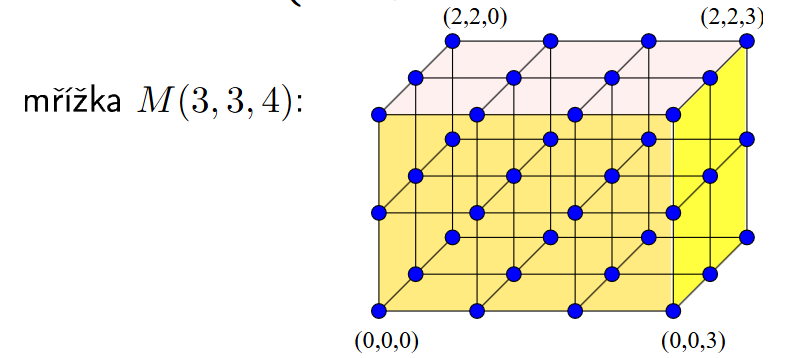
• Základní vlastnosti
  • Hierarchicky rekurzivní (konstrukce kartézským součinem jednorozměrných řetízků)
  • Není regulární, proto ani uzlově symetrická
  • Bipartitní, ne vždy vyvážená
  • Obsahuje hamoltonovskou kružnici při aspoň jedné sudé dimenzi
  • Manhattanská vzdálenost uzlů (metrika): pohyb mezi uzly po ortogonálních hranách
  • V praxi nejčastěji 2D (čipy) a 3D (server rack)
  • Směrování posunem seřazeným po dimenzích

n-Rozměrný toroid

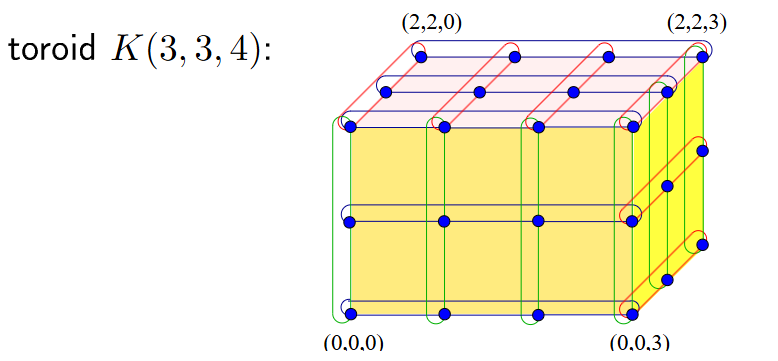
• Zabalená mřížka, n-rozměrná kružnice
• Základní vlastnosti
  • Není hierarchicky rekurzivní
  • Uzlově symetrický
  • Bipartitní pokud jsou všechny rozměry sudé
  • Průměrná vzdálenost poloviční oproti mřížce
  • Bisekční šířka dvojnásobná oproti mřížce (řez kružnice vs. řetězu)
  • Obsahuje hamiltonovskou kružnici vždy
  • Manhattanská vzdálenost uzlů

n-Rozměrná hyperkrychle

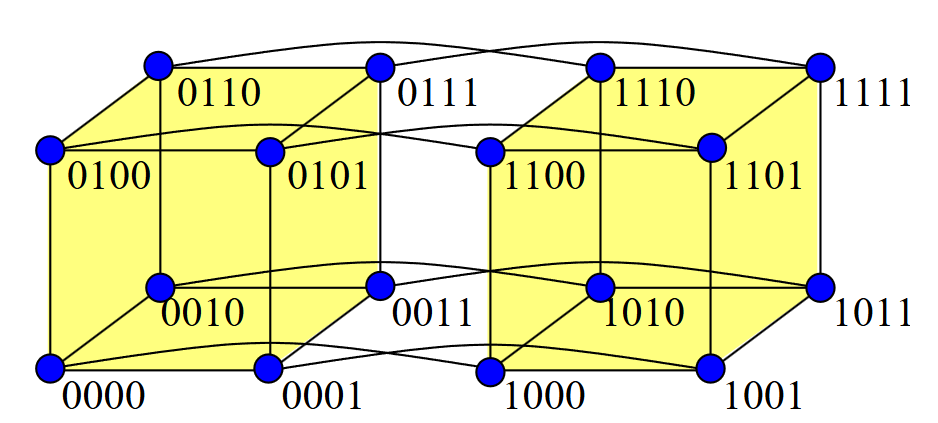
• Základní vlastnosti
  • Hustá: stupeň uzlů je logaritmický - náročná na HW
  • Hierarchicky rekurzivní
  • Uzlově symetrická
  • Bipartitní
  • Optimálně souvislá (uzlová = hranová)
  • Hrany mezi uzly o hammingově vzdálenosti 1 (např. 1000-1001)
• Základní testovací topologie díky své optimální souvislosti
• Má ale logaritmický stupeň uzlů a je škálovatelná jen po mocninách 2
• Směrování seřazením cest lexikograficky (e-cube)

Hyperkubické propojovací sítě

Řídké hyperkubické propojovací sítě

• Konstantní stupeň uzlů a logaritmický průměr
• Horší škálovatelnost než hyperkrychle
• Přirozená topologie pro mnoho paralelních algoritmů
• Motýlek je nativní topologie pro provádění tzv. normálních hyperkubických algoritmu
  • V každém paralelním kroku algoritmu jsou použity pouze hrany jedné dimenze hyperkrychle

Zabalený motýlek

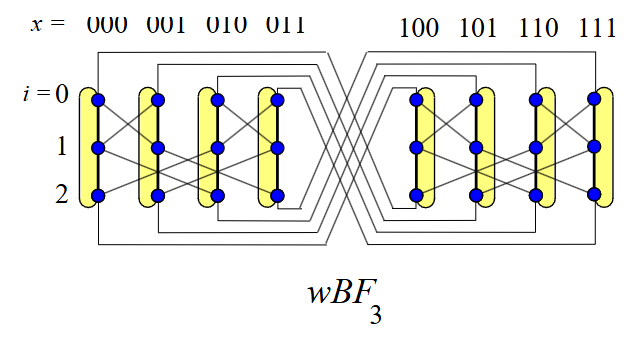
• Základní vlastnosti
  • Není hierarchicky rekurzivní - kružnici nerozložíš
  • Uzlově symetrický
  • Vyvážený bipartitní pro sudá n
  • Hamiltonovský
  • Konstantní stupeň uzlu 4
  • Každý uzel má dvě hrany ve vlastní kružnici a dvě hrany do vedlejších kružnic
  • Optimální průměr a průměrné vzdálenosti: nejhůř projdeme n hyperkubických hran a $⌊n/2⌋$ na druhou stranu kružnice

Obyčejný motýlek

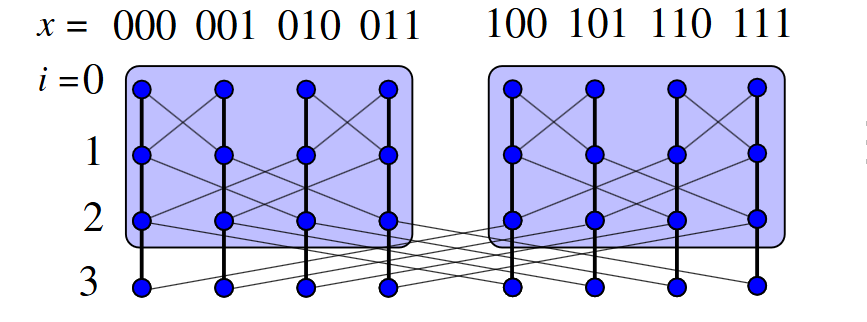
• Dva druhy hran: přímé a křížové (hyperkubické).
• Vznikne ze zabaleného motýlka rozdělením 0. vrcholu kružnic na dva uzly
• Základní vlastnosti
  • Hierarchicky rekurzivní
  • Není regulární, proto ani uzlově symetrický
  • Bipartitní
  • Není hamiltonovský
  • Vznikne ze zabaleného motýlka rozdělením 0. vrcholu kružnic na dva uzly
  • Směrování e-cube (existuje jediná nejkratší cesta mezi dvěma uzly)
  • Minimální permutační síť

Vnořeni

• Mějme množinu procesoru která provádí paralelní algoritmus
• Známe velikost a strukturu grafu procesu
• Máme známou propojovací sit
• Otázka je: Jak mapovat graf procesu na tento stroj aby vypočet byl co nejefektivnější
• Měřeni kvality vnoření
  • Maximální zatížení cílového uzlu – maximální počet zdrojových vrcholů namapovaných na jeden cílový uzel
    • Maximální počet procesů, který bude přidělen 1 procesoru
    • Chceme stejnoměrné zatížení (liší se max o 1)
  • Expanze vnoření – poměr velikosti cílové sítě (= počet výpočetních uzlů) a velikosti zdrojového grafu (=počet procesů)
    • Větší expanze implikuje dražší simulace
    • Chceme blízkou 1 při jedničkovém zatížení a snižujeme úměrným rovnoměrným zvětšením zatížení uzlů
  • Maximální dilatace zdrojových hran v cílové síti – maximální délka obrazů zdrojových hran v cílové síti
    • Po jak dlouhých cestách budou muset v cílovém počítači putovat zprávy posílané mezi procesy, které jsou v zdrojovém grafu sousední
    • Sledujeme, pokud máme přepínání citlivé na vzdálenosti, jinak průměrná dilatace
  • Maximální zahlcení cílové hrany
    • Linkové zahlcení – maximální počet obrazů zdrojových hran procházejících skrz cílové linky
    • Uzlové zahlcení – maximální počet obrazů zdrojových hran procházejících skrz cílové uzly
    • Spíš sledujeme průměrné zahlcení
• Kvaziizometrická topologie – sítě 𝐺 a 𝐻 jsou kvaziizometrické, pokud 𝐺 může být vnořen do 𝐻 a naopak s konstantními měřítky vnoření
  • 𝐺 a 𝐻 jsou výpočetně ekvivalentní, pokud jedna může může simulovat druhou s konstantním zpomalením (implikováno kvaziizometrií)
  • Obyčejný motylek a Zabaleny motylek jsou kvaziizometricke
  • Mřížka a Toroid jsou kvaziizometrické
• Hyperkrychle simuluje optimálně většinu topologií
• Toroidy jsou kvaziizometrické s mřížkami stejných rozměrů