4. Integrál funkcí více proměnných (Darbouxova konstrukce). (NI-MPI)

---

Integrál funkcí více proměnných

• Geometricky význam: Hlavní myšlenka konstrukce je aproximace plochy pod křivkou pomocí obdélníků
  1. Interval rozdělíme na malé kousky (tzv. rozdělení intervalu)
  2. Na těchto kouscích aproximujeme funkci $f(x)$ vhodně zvolenými konstantními funkcemi (dostaneme takzvané stupňovité funkce)
  3. Obsah pod grafem stupňovité funkce je součet obsahu obdélníků, a tedy snadno spočítatelná veličina.

Rozdělení intervalu

• Mějme interval $[a,b]$ který chceme rozdělit.
  • Vytvoříme si konečnou množinu $\sigma = \{x_0,x_1,...,x_n\}$ takovou ze platí pro všechny prvky v množině: $a=x_0<x_1<...<x_n = b$. Tak tomuto říkáme rozděleni intervalu $[a,b]$. Bodům $k:\quad x_k, k \in \{1,2,...,n-1\}$ říkáme dělicí body.
  • Normu rozdělení nazýváme číslo které určuje největší vzdálenost mezi intervaly, tedy: $$v(\sigma) = \text{max}\{\Delta_k: k=1,2,...,n\},\quad \text{kde}\ \Delta_k = x_k-x_{k-1},\quad k=1,2,...,n$$
  • Ekvidistantní rozdělení je takové rozděleni kde $\text{max}\{\Delta_k: k=1,2,...,n\} = \text{min}\{\Delta_k: k=1,2,...,n\}$

Darbouxův integral

Darbouxův součet

• Mějme funkci $f$ která je definovaná na intervalu $[a,b]$ a $\sigma = \{x_0,x_1,...,x_n\}$ je rozděleni intervalu.
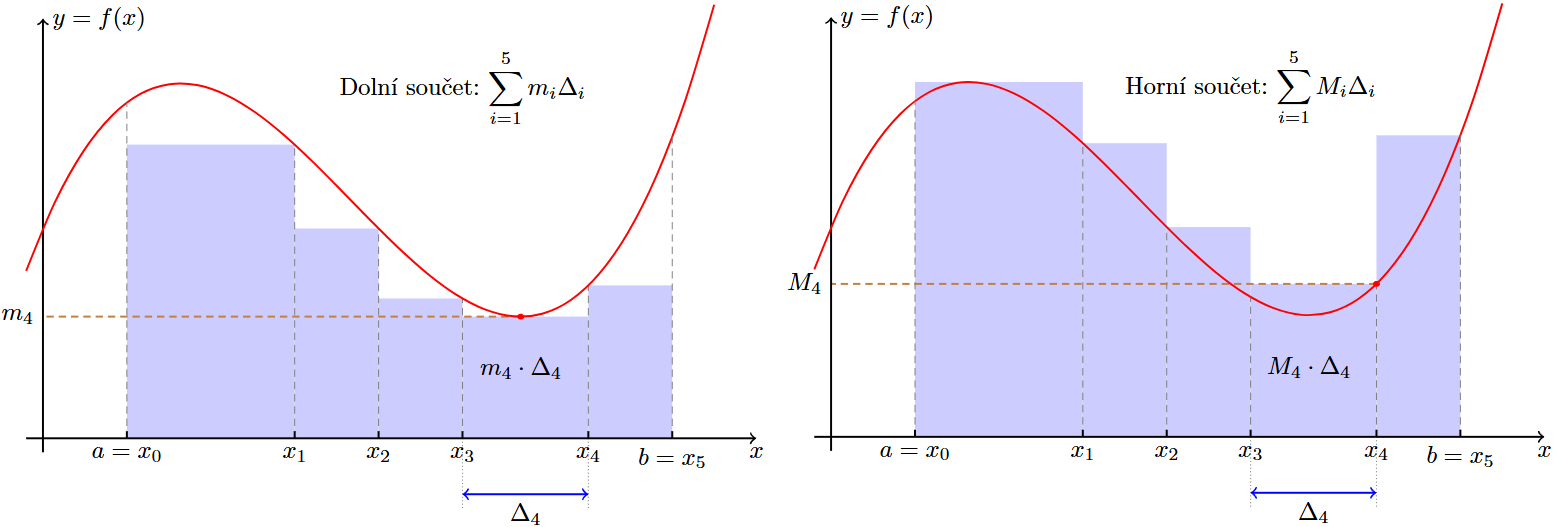
• Pro to abychom spočetly plochu pod grafem máme dvě moznosti bud tak ze pro každý kus rozděleni $\sigma$ spočteme supremum a nebo infimum. To nám da dolní a horní hranici pro plochu pod grafem.
  • Horní součet: $$M_i=\text{sup}_{x\in[x_i-1,x_i]}f(x)\quad\quad\rightarrow\quad\quad S_f(\sigma)=\sum_{i=1}^nM_i\Delta_i$$
  • Dolní součet: $$m_i=\text{inf}_{x\in[x_i-1,x_i]}f(x)\quad\quad\rightarrow\quad\quad s_f(\sigma)=\sum_{i=1}^nm_i\Delta_i$$

Darbouxův integral

• Mějme funkci $f$ která je definovaná na intervalu $[a,b]$ a $\sigma = \{x_0,x_1,...,x_n\}$ je rozděleni intervalu.
• Pokud chceme vypočítat integral této funkce na danem intervalu musíme Darbouxův součet dělat s rozdělením intervalu limitně se blížícím k nekonečnu.
• Horní Darbouxův integrál (funkce $f$ na $[a, b]$) je: $$D_f = \text{inf} \{S_f(\sigma):\sigma \text{ je rozdělení } [a,b]\}$$
• Dolní Darbouxův integrál (funkce $f$ na $[a, b]$) je: $$d_f = \text{sup} \{s_f(\sigma):\sigma \text{ je rozdělení } [a,b]\}$$
• Darbouxův integrál (funkce $f$ na $[a, b]$) je: $$\int_a^b f(x)dx = D_f = d_f$$
• Mějme funkci $f$ která je spojitá na intervalu $[a,b]$. Potom existuje $\int_a^bf(x)dx$. Je-li $\sigma_n$ normální posloupnost ( $\lim_{n\rightarrow\infty} v(\sigma_n)=0$ ) Potom existuji: $$\lim_{n\rightarrow\infty} s_f(\sigma_n)\quad\quad\land\quad\quad \lim_{n\rightarrow\infty} S_f(\sigma_n)=0$$ a jsou rovny $\int_a^bf(x)dx$

Vlastnosti Darbouxova integrálu

Aditivita integrálu

• Nechť $f$ a $g$ jsou spojité funkce na intervalu $[a, b]$. Potom pro integrál funkce $f + g$ (která je také automaticky spojitá na $[a, b]$) platí: $$\int_a^b(f+g)(x)dx = \int_a^bf(x)dx + \int_a^bg(x)dx$$ Multiplikativita integrálu

• Nechť $f$ je spojitá na intervalu $[a, b]$ a $c \in \mathbb{R}$ je konstanta. Potom pro integrál funkce $cf$ platí: $$\int_a^b(cf)(x)dx = c\int_a^bf(x)dx$$

Darbouxův integral vice proměnných

Darbouxův integral vice proměnných nad obdélníkovou oblasti

• Mějme funkci $f$ která je definovaná na intervalu $[a,b]$, $\sigma_x = \{x_0,x_1,...,x_n\}$ a $[c,d]$, $\sigma_y = \{y_0,y_1,...,y_m\}$. Dale definujeme rozdělení $\sigma = \sigma_x \times \sigma_y$ coz je rozdělení (Kartézský součin): $D = [a,b] \times [c,d]$
• Horní Darbouxova suma $f$ vzhledem $k$ rozdělení $\sigma$ je: $$M_{i,j} = \text{sup}\{f(x,y): (x,y) \in [x_{i-1},x_i]\times [y_{j-1},y_j]\}\rightarrow S_f(\sigma) =\sum_{i-1}^n\sum_{j=1}^m M_{i,j}(x_i-x_{i-1})(y_j-y_{j-1})$$

• Dolní Darbouxova suma $f$ vzhledem $k$ rozdělení $\sigma$ je: $$m_{i,j} = \text{inf}\{f(x,y): (x,y) \in [x_{i-1},x_i]\times [y_{j-1},y_j]\}\rightarrow s_f(\sigma) =\sum_{i-1}^n\sum_{j=1}^m m_{i,j}(x_i-x_{i-1})(y_j-y_{j-1})$$

• Horní Darbouxův integrál (funkce $f$ na $D$) je (minimum maxima): $$D_f = \text{inf}\{S_f(\sigma): \sigma\text{ je rozdeleni }D\}$$

• Dolní Darbouxův integrál (funkce $f$ na $D$) je (maximum minima): $$D_f = \text{sup}\{s_f(\sigma): \sigma\text{ je rozdeleni }D\}$$
• Dvojitý Darbouxův integrál (funkce $f$ na $D$) je: $$\iint_Df(x,y)dxdy = D_f = d_f$$

Darbouxův integral vice proměnných nad obecnou oblastí

• Funguje to na principu ze uzavřeme obecnou oblast do obdélníkové oblasti. Tuto novou oblast definujeme jako $\tilde D$. Dale definujeme novou funkci $\tilde f$ pro místa která patří do původní oblasti definujeme novou funkci jako funkci původní a v ostatních oblastech ji dame rovnou $0$.
  • Mějme $f: D \rightarrow \mathbb{R}$, kde $D \subset{\tilde D} = [a,b] \times [c,d]$. Definujeme dvojitý Darbouxův integral funkce $f$ na $D$ jako hodnotu: $$\iint_Df := \iint_{\tilde{D}}\tilde f$$ kde nova funkce $\tilde f (x)$ je definovaná jako: $$\tilde{f}(x) = \begin{cases} f(x) & \text{pro } x \in D \\ 0 & \text{pro } x \notin \tilde D \setminus D \end{cases}$$ pokud existuje

Vlastnosti

• Množina míry nula – je pro hodnotu integrálu zanedbatelná (Tedy taková množina která je tak malá ze nemá vliv na integraci.)
• Funkce je integrabilní pokud $f$ je spojitá skoro všude. (Ma míru nula v nespojitých částí)
• Pokud $D = D_1 ∪ D_2$, kde $D_1$ i $D_2$ jsou uzavřené omezené množiny, $D_1 ∩ D_2$ má míru nula a $f$ je integrabilní na $D$, pak platí: $\iint_Df = \iint_{D_1}f+\iint_{D_2}f$
• Platí-li pro (skoro) všechna $(x, y) \in D$ a pro integrabilní funkce $f_1$ a $f_2$, že $f_1(x, y) \leq f_2(x, y)$, potom: $\iint_Df_1\leq\iint_Df_2$
• Pro $c \in \mathbb{R}$ a integrabilní funkci $f$ platí: $\iint_Dc\cdot f(x,y)dxdy = c\cdot \iint_Df(x,y)dxdy$

Vypočet integrálů

Newtonova metoda

• Mějme funkci $f$ spojitou na intervalu $[a,b]$ a primitivní funkci $F$ která aproximuje integral v intervalu $[a,b]$ pak: $$\int_a^bf(x)dx = F(b)-F(a) = [F(x)]_a^b$$

Výpočet dvojného integrálu nad obdélníkovou oblastí

• Jedna se vlastně o postupnou integraci tedy
  • Buď $f (x, y)$ integrabilní funkce na $D = [a, b] \times [c, d]$. Pokud existuje jeden z integrálů $$\int_a^b(\int_c^d f(x,y)dy)dx \quad \quad \quad \int_c^d(\int_a^b f(x,y)dx)dy$$ pak je roven dvojnému integrálu: $$\iint_D f(x,y)dxdy$$

Výpočet dvojného integrálu nad obecnou oblastí

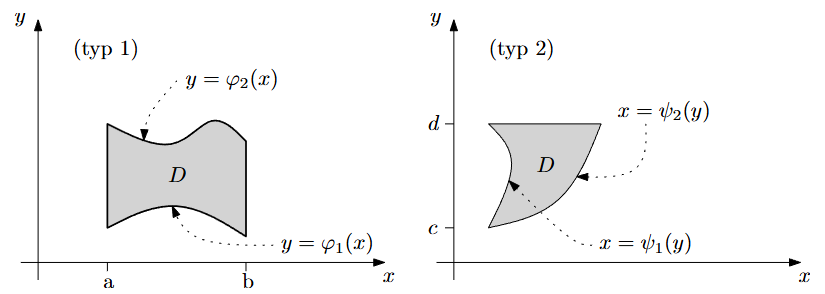
• Pro tento typ integrálů máme dvě moznosti interval omezeny funkcemi ze shora a spodu a nebo z prava a leva:
  • (typ 1) $x$ je z intervalu $[a, b]$ a $y$ je omezené spoj. funkcemi $φ_1(x)$ a $φ_2(x)$ splňujícími $φ_1(x) ≤ φ_2(x)$,
  • (typ 2) $y$ je z intervalu $[c, d]$ a $x$ je omezené spoj. funkcemi $ψ_1(y)$ a $ψ_2(y)$ splňujícími $ψ_1(y) ≤ ψ_2(y)$.

• Na vypočet nám slouží rovnice:
  • Je-li $D$ typu 1, máme: $$\iint_D f(x,y)dxdy = \int_a^b(\int_{φ_1(x)}^{φ_2(x)}f(x,y)dy)dx$$
  • Je-li $D$ typu 2, máme: $$\iint_D f(x,y)dxdy = \int_c^d(\int_{ψ_1(y)}^{ψ_2(y)}f(x,y)dx)dy$$