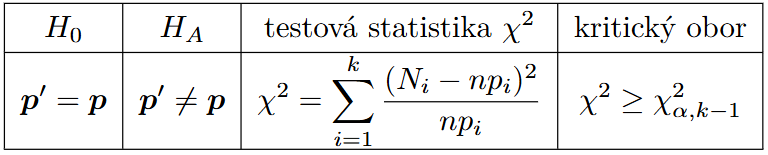6. Testování statistických hypotéz. T-testy, testy nezávislosti, testy dobré shody. (NI-VSM)¶

Základní pojmy¶

Important

Vždy máme dvě hypotézy:
- Nulová hypotéza $H_0$ označuje tvrzení, o kterém chceme rozhodovat.
- Alternativní hypotéza $H_A$ je opačné tvrzení, které v rozhodovacím procesu stavíme proti $H_0$
Předpokládáme, že ve skutečnosti platí buď $H_0$ nebo $H_A$ .
Typy chyb:
- Zamítneme $H_0$ , ačkoli platí – chyba prvního druhu.
- Nezamítneme $H_0$ , ačkoli neplatí a ve skutečnosti platí $H_A$ – chyba druhého druhu.
- Chceme, aby pravděpodobnost chyby 1. druhu byla nejvýše rovna zvolené hodnotě $α$

Výsledek testovaní
- Testujeme hypotézu $H_0$ proti alternativě $H_A$ na hladině významnosti $\alpha$ .
- Zamítnutí $H_0$ ve prospěch $H_A$ je silný výsledek!
- Jestliže zamítáme $H_0$ , můžeme s velkou spolehlivostí tvrdit, že platí alternativa $H_A$
- Je-li pak výsledkem testu zamítnutí $H_0$ , víme, že $H_A$ platí s pravděpodobností alespoň $1 − \alpha$ .
Hranice/Hladina významnosti
- Jedna se o maximální přijatelnou pravděpodobnost chyby I. druhu
- Značíme $\alpha$

Important

Matematicky
- Máme náhodný vektor $X = (X_1,X_2,...X_n)^T$ které ma nějaké rozdělení
- Množina všech možných rozdělení vektoru $X$ je genericky: $P=\{P_\theta:\theta \in \Theta\}$
- Tato množina $P$ se potom rozděluje na dvě disjunktní množiny: $H_0 \cup H_A =P$
Centralni limitni veta
- Tato veta rika ze kdyz udelame dostatecne hodne nahodnych vyberu tak rozdělení výběrového průměru blíží k normálnímu rozdělení
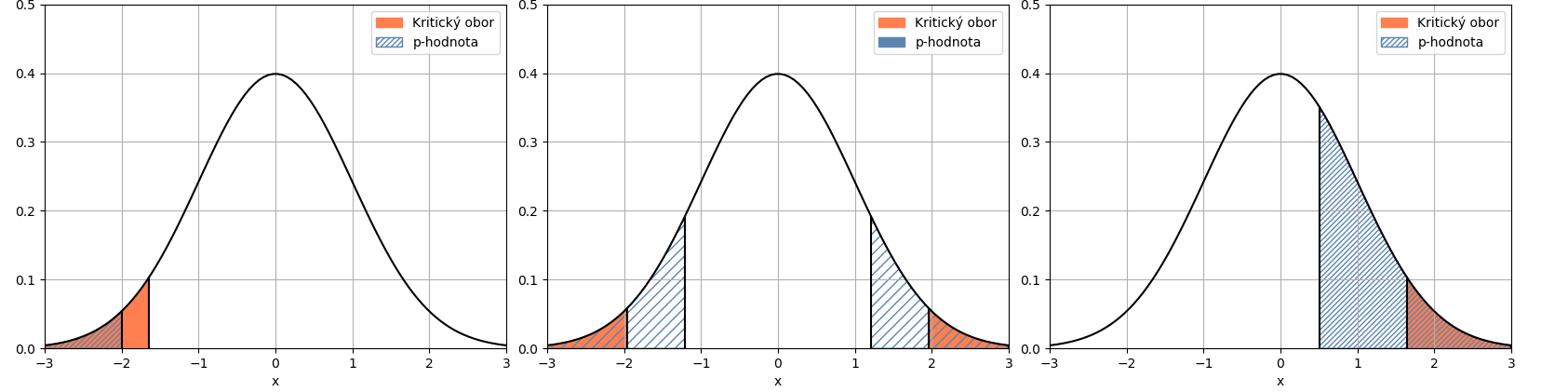
Kritický obor
- Všechny moznosti pro $X$ při kterých bychom zamítly $H_0$ nazveme Kritický obor a značíme ho $W_\alpha$
- Chyba prvního druhu je nejvýše $\alpha$ tedy:
  - $P_\theta(x \in W_\alpha)\leq \alpha \text{ pro kazde } \theta \in \Theta_0$
p-hodnota
- Jedna se vlastně o nejnižší $\alpha$ při kterém dokážeme zamítnout $H_0$
- Značíme: $\hat p \equiv \hat p (X) = inf\{\alpha | X \in W_\alpha\}$
- Význam p-hodnoty
  - Takže pokud p-hodnota $\leq \ \alpha$ tak nedokážeme zamítnout $H_0$

Pasted image 20250119145701.png

Hypotézy a jejich typy
- Parametrické – test se týká neznámých paramterů a vycházíme ze známeho rozdělení.
- Neparametrické – test různých vlastností rozdělení – nezávislost apod. $X$ má obecné rozdělení.

Testování pomocí intervalů spolehlivosti¶

Uvazujeme náhodný výběr: $X=(X_1,X_2,...,X_n)^T$
Důležité je aby vyber byl nezávislí a stejně rozdělený
Máme konfidenční interval $(L(x),U(X))$
Zamítáme hypotézu $H_0$ jestliže $\theta \notin (L,U)$
Pro oboustranný test musíme vybrat hladinu významnosti: $\alpha/2$ pro horní a dolní hranici.
Pro jednostrany test bereme ze jedna strana je $\infty$ a druha je omezeny interval kde nastavujeme hladinu významnosti na $\alpha$

Important

Obecný postup¶

Najdeme funkci náhodného výběru a parametru, $H_\theta ≡ H\theta(X_1, . . . , X_n)$ , která má známé rozdělení.
Vezmeme její kritické hodnoty $h_{1−\alpha/2}$ a $h_{\alpha/2}$ , pro které $P (h_{1−\alpha/2} < H_\theta < h_{\alpha/2} ) = 1 − \alpha$ .
Úpravou nerovností vyjádříme $\theta$ a získáme $P (L < \theta < U ) = 1 − \alpha$ , kde $L$ a $U$ už jsou funkce pouze náhodného výběru, tj. statistiky.

Při konstrukci statistiky $H_\theta$ se často využívá vhodný bodový odhad $\theta$ , např. výběrový průměr pro střední hodnotu nebo výběrový rozptyl pro rozptyl.

Testovaní pomoci intervalu normální rozděleni¶

Interval spolehlivosti pro střední hodnotu při známém rozptylu
- Neznáme $𝜎^2$ → odhadujeme ho pomocí výběrového rozptylu $𝑠_n^2$
- ( Výběrová střední hodnota - kritická hodnota standartního rozděleni * chyba průměru, Výběrová střední hodnota + kritická hodnota standartního rozdělení * chyba průměru)
- $\left(\bar{X}_n - z_{\alpha/2}\frac{ \sigma}{\sqrt{n}}, \bar{X}_n + z_{\alpha/2} \frac{ \sigma}{\sqrt{n}}\right)$
Interval spolehlivosti pro střední hodnotu při neznámém rozptylu
- Používá studentovo t-rozděleni
- $\left(\bar{X}_n - t_{\alpha/2,n-1}\frac{ \sigma}{\sqrt{n}}, \bar{X}_n + t_{\alpha/2,n-1} \frac{ \sigma}{\sqrt{n}}\right)$
Interval spolehlivosti pro rozptyl
- TODO vzoreček

T-Testy¶

Important

Základem T-testu je studentovo rozdělení.
Používáme k testu Testovou statistiku která ma obecný tvar: $T = \frac{\text{ Rozdil vyberove stredni hodnoty a stredni hodoty hypotezy}}{\text{Rozptyl}}$
Jsou 3 základní testy: jedno výběrový, párový a dvou výběrový

Jedno výběrový t-test
- Testujeme střední hodnotu a známe rozptyl.
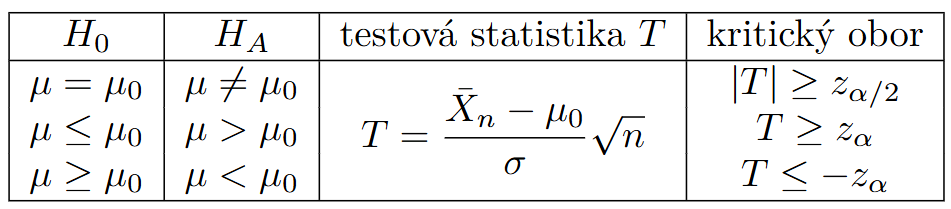
- Testujeme střední hodnotu a neznáme rozptyl.
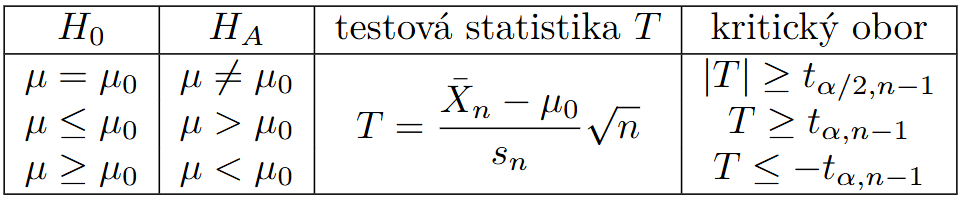
- Testujeme rozptyl
Párový t-test
- Porovnavaji se dve zavisle datove sady
- Pozorujeme náhodný vyber: $(X_1,Y_1)^T,...,(X_n,Y_n)^T$ a chceme vedet
  - $H_0: \mu_1=\mu_2$
  - $H_A: \mu_1\neq\mu_2$
- Rozdíl výběrové a střední hodnoty hypotézy je vlastně rozdíl $X_i-Y_i$ střední hodnoty jsou tak: $\mu_\Delta=\mu_1-\mu_2$
- Pokud budeme předpokládat ze $Z_i\sim N(\mu_\Delta,\sigma^2)$ kde $\sigma^2$ neznáme.
  - Muzeme toto pak prevest na test jednovyberovy kde $\mu_\Delta=0$ a vychazi tak:
Dvouvýběrový t-test
- Porovnávají se dvě nezávisle datové sady
- Důležité je ze ve jmenovateli je rozdíl středních hodnoty každé sady
- Stejné rozptyly: $H_0:\mu_1=\mu_2$
- Různé rozptyly: $H_0:\mu_1\neq\mu_2$

Test nezávislosti v kontingenčních tabulkách¶

Important

Testujeme zda dvě sady pozorovaní jsou na sobe nějak závisle
- $H_0:\quad p_{i\bullet}\cdot p_{\bullet j} = p_{ij}$
- $H_A:\quad p_{i\bullet}\cdot p_{\bullet j} \neq p_{ij}$

Mějme náhodný vektor $X = (Y, Z)^T$ s diskrétním rozdělením, přičemž veličina $Y$ nabývá hodnot $1, . . . , r$ a veličina $Z$ nabývá hodnot $1, . . . , c$ .

Test dobré shody¶

Important

Zjišťujeme jestli naše pozorované rozdělení odpovídá nějakému teoretickému rozděleni.
Můžeme si to představit tak ze máme teoretické rozdělení
- Toto teoretické rozděleni rozdělíme do binů nějaké velikost
- Rozdělíme jednotlivé pozorované rozdělení do daných binů
- Zjišťujeme zda naše rozděleni ma stejné rozložení jako to teoretické
Chceme co největší počet binů.
- Cim víc jich je tím vice potřebujeme pozorovaní
- Vytváříme tolik binů aby teoretické četnosti byly alespoň 5

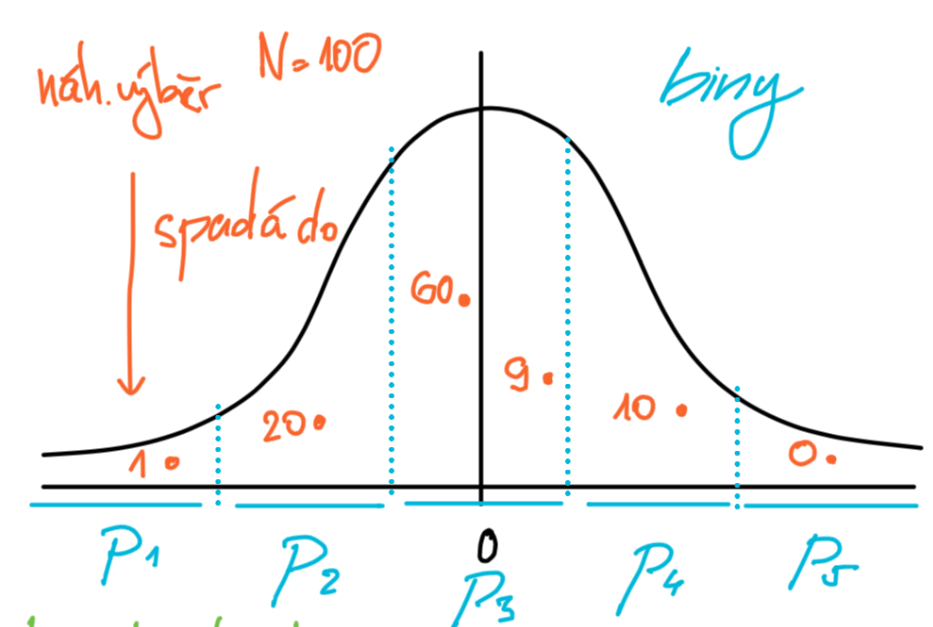
Pasted image 20250119151304.png

Multinomické rozdělení¶

Máme náhodnou veličinu která nabývá hodnot $1,...,k$ uděláme náhodný vyber, spočítáme četnosti a dostaneme tak náhodné veličiny $N_1,...,N_k$ kde $N_i$ je počet vyberu $i$ při náhodném vyberu.
Testujeme ze skutečně hodnoty pravděpodobností jsou $p_1,...,p_k$