7. Základy teorie informace a kódování, entropie. (NI-VSM)

---

Základní pojmy

• Množinu hodnot (nejvýše spočetnou), kterých $X$ nabývá, budeme značit $\mathcal{X}$
• Pravděpodobnostní funkci veličiny $X$ v bodě $x \in \mathbb{R}$ budeme značit $p(x)$, tj. pro každé $x \in \mathbb{R}$ bereme $p(x) = P(X = x)$

Entropie

• Jedna se o míru neurčitosti, definice entropie diskrétní náhodné veličiny: $$H(X) =-\sum_{x\in\mathcal{x}}p(x)\log p(x)$$
• Funkcí $\log x$ zde konvenčně značíme logaritmus čísla $x$ o základu $2$, tj. $\log_2 x$
• Všimněme si, že číselné hodnoty $X$ se v definici entropie vůbec nevyskytují. Jsou zde pouze pravděpodobnosti jednotlivých hodnot.
  • Entropie je tak invariantní vůči libovolné transformaci hodnot, která ponechá jejich pravděpodobnosti. Tj. pro libovolnou funkci $g$ prostou na $X$ platí $H(X) = H(g(X))$

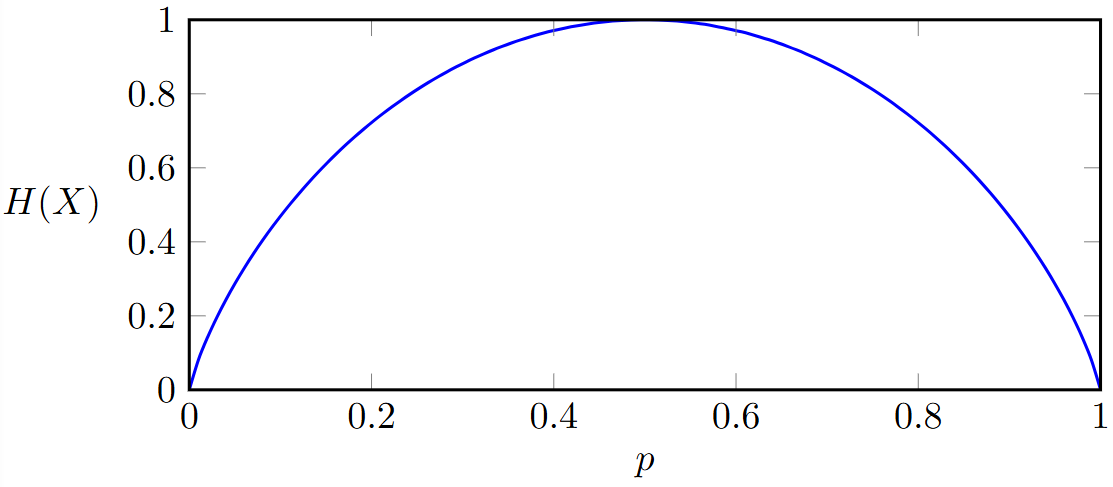
Entropie jako očekávaná míra neurčitosti

• Entropii $H(X)$ můžeme chápat jako střední hodnotu: $$H(X) = - E \log p(X) = EI(X)$$ kde $$I(x) = -\log p(x)$$ a $I(x)$ se nazývá vlastní informace nebo míra neurčitosti hodnoty $x$
• Vlastnosti
  • $H(X) \geq 0$
  • Entropie je konkávní funkcí rozdělení.
  • V deterministických případech $p = 0$ a $p = 1$ je entropie $0$
  • Maximum entropie nastává pro rovnoměrné rozdělení, kdy je největší míra neurčitosti.

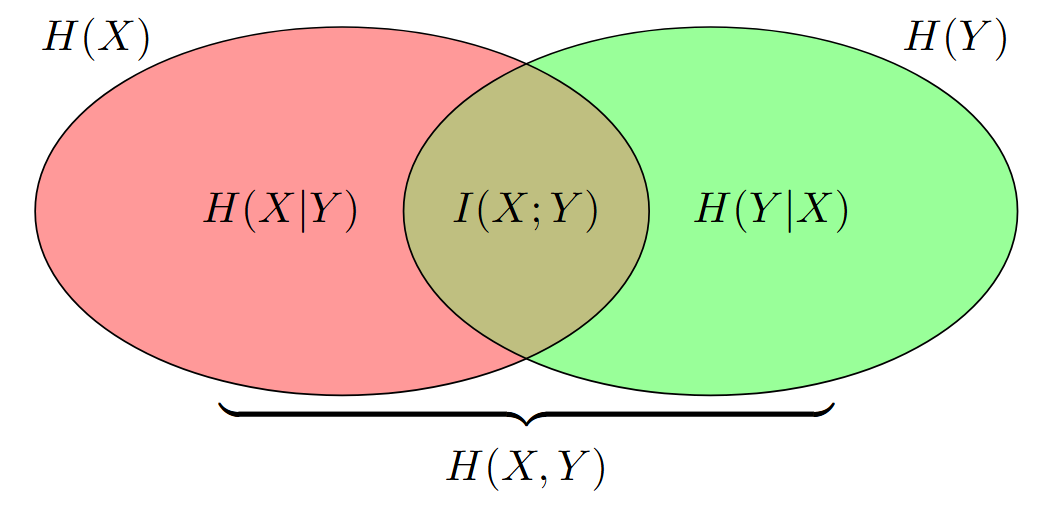
Sdružená entropie

• Sdružená entropie $H(X, Y )$ diskrétních náhodných veličin $X$, $Y$ se sdruženým rozdělením $p(x, y)$ je definována jako: $$H(X) = -\sum_{x\in \mathcal{X}}\sum_{y \in \mathcal{Y}} p(x,y)\log p(x,y)$$
• Alternativně můžeme vyjádřit sdruženou entropii pomoci střední hodnoty: $$H(X) = -E\log p(X,Y)$$

Podmíněná entropie

• Podmíněná entropie $H(Y |X)$ diskrétních náhodných veličin $X$, $Y$ se sdruženým rozdělením $p(x, y)$ je definována jako: $$H(Y|X) = -\sum_{x\in \mathcal{X}}\sum_{y \in \mathcal{Y}} p(x,y)\log p(y|x)$$
• Alternativně můžeme vyjádřit podmíněnou entropii pomoci střední hodnoty: $$H(Y|X) = -E\log p(Y|X)$$

Relativní entropie

• Jedna se o míra odlišnosti mezi dvěma pravděpodobnostními rozděleními.
• Relativní entropie nebo Kullback-Leiblerova vzdálenost $D(p||q)$ mezi diskrétním rozdělením $p$ a diskrétním rozdělením $q$ na množině $X$ je definována vztahem: $$D(p||q) =\sum_{x \in \mathcal{X}} p(x)\log \frac{p(x)}{q(x)}$$
• Vlastnosti
  • Nabývá hodnoty $0$, právě když se distribuce $P$ a $Q$ rovnají skoro všude

Vzájemná informace

• Vzájemná informace $I(X; Y )$ diskrétních náhodných veličin $X$ a $Y$ je definována vztahem: $$I(X;Y) =\sum_{x \in \mathcal{X}} \sum_{y \in \mathcal{Y}} p(x,y)\log \frac{p(x,y)}{p(x)p(y)}$$
• Vlastnosti
  • Je symetrická tedy $I(X;Y) = I(Y;X)$
  • Jedná se tedy o relativní entropii skutečného sdruženého rozdělení a rozdělení nezávislých veličin se stejnými marginálami: $I(X;Y) = D(p(x,y)||p(x)p(y))$

Important

Jensenova nerovnost

• Jedna se o souvislost konvexity a střední hodnoty
• Buď $f$ konvexní funkce a $X$ náhodná veličina. Potom platí: $$Ef(X) \geq f(EX)$$

Informační nerovnost

• Buď $p(x)$ a $q(x)$ pro $x \in \mathcal{X}$ dvě možná rozdělení diskrétní náhodné veličiny $X$. Potom: $$D(p||q) \geq 0$$
• Důsledky:
  • Nezápornost vzájemné informace
    • $I(X, Y) = 0$ pokud $X$ a $Y$ jsou nezávisle
  • Maximalizace entropie
    • $H(X)\leq \log|X|$ kde $|X |$ značí počet prvků množiny $\mathcal{X}$
  • Podmiňování redukuje entropii
    • $H(X|Y) \leq H(X)$

Teorie informace a kódovaní

• Teorie kódování jakožto část teorie informace se zabývá problémem, jak zapsat zdrojovou zprávu (informaci) do posloupnosti symbolů, které jsme schopni přenášet, tak, aby byl následný přenos co nejefektivnější (největší komprese, nejmenší náchylnost k chybám).

Kód

• Máme množinu kterou chceme zobrazit do množiny konečných řetězců symbolů.
• Zobrazení $C : X → D^∗$ množiny $\mathcal{X}$ do množiny $D^∗$ konečných řetězců symbolů D-ární abecedy $\mathcal{D}$ nazýváme (D-ární) kód diskrétní náhodné veličiny X.
• Obraz $C(x)$ prvku $x \in \mathcal{X}$ nazýváme kódové slovo příslušející prvku $x$ a jeho délku značíme $\ell(x)$.
• Množina $\mathcal{D}^*$ je tedy definována jako $$D^* = \bigcup_{k=1}^{\infty} D^k$$ kde $D^k$ označuje řetězce symbolů z $D$ délky $k$

Střední délka kódu

• Střední délku $L(C)$ kódu $C$ náhodné veličiny $X$ s rozdělením $p(x)$ definujeme jako: $$L(X) = \sum_{x\in\mathcal{X}}\ell(x)p(x)$$

Typy kódů

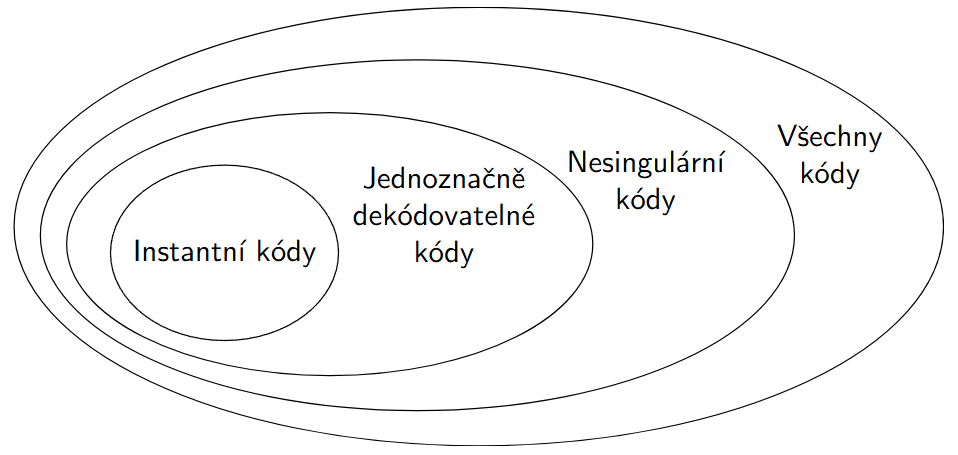
• Singulární kódy
  • Kody které jsou pouze podle definice tedy můžou se klidně opakovat
• Nesingulární kódy
  • Kody mají jednoznačnou dekódovatelné zobrazeni.
  • Pokud dostaneme jeden znak dokážeme ho dekódovat
  • Pokud ale dostaneme posloupnost kódů tak už ji nemusíme byt schopni dekódovat
  • Kód $C$ diskrétní náhodné veličiny $X$ je nesingulární, pokud je $C$ prosté zobrazení.
    • pro každé $x, x^′ \in X$ platí: $x\neq x' \Rightarrow C(X) \neq C(x')$
• Jednoznačně dekódovatelný kód
  • Pokud dostaneme posloupnost kódů tak jsme schopni dekódovat cely řetězec kódových slov:
  • Pokud $C^*(x_1,x_2,...x_n) = C(x_1)C(x_2)...C(x_n)$. Tak pak musí $C^*$ byt nesingulární
• Instantní kód
  • Jedna se o kódy které jsou snadno dekódovatelné
  • Kód nazýváme instantní (prefixový) pokud žádné kódové slovo není prefixem jiného kódového slova.

x	Singulární	Nesingulární	Jednoznačně dekódovatelný	Instantní
1	0	0	10	0
2	0	010	00	10
3	1	01	11	110
4	1	10	110	111

Kraftova nerovnost

• Pro libovolný instantní kód nad D-ární abecedou musí délky kódových slov $ℓ_1, ℓ_2, ... , ℓ_n$ splnit nerovnost: $$\sum_iD^{-\ell_i} \leq 1$$
• Navíc, ke každé n-tici délek, které splní tuto nerovnost, existuje instantní kód s kódovými slovy těchto délek.
• McMillan: toto platí i pro jednoznačně dekódovatelné kódy, takže ubráním požadavku instantní dekódovatelnosti si nepřidáme další možnosti délek kódových slov - řešení optimality instantních kódů řeší i optimalitu jednoznačně dekódovatelných

Optimální kódy

• Střední délka instantního kódu je vždy vetší nebo rovna entropii kódu: $$L(C) \geq H_D(X)$$ Rovnost nastává pokud $D^{-\ell_i} = p_i$
• Optimální kód je takový kód který ma nejmenší střední délku
• Dale platí ze optimální kód ($C^*$) se může od entropie kódu vzdálit maximálně o $1$ tedy: $$H_D(X) \leq L(C^*) < H_D(X)+1$$

Huffmanovo kódování

• Jedna se o algoritmus pro vytvořeni optimálního instantního kódu
• Algoritmus:
  • Spojíme dvě nejméně pravděpodobné hodnoty do jedné a uvažujme nové rozdělení náhodné veličiny s o jednu menším počtem hodnot.
  • Opakujeme tak dlouho, až zůstane jediná hodnota, které přiřadíme prázdný řetězec jako kódové slovo.
  • Zpětným chodem zkonstruujeme kódová slova všech původních hodnot.
  • Pro hodnotu $x$, která vznikla spojením hodnot $u$ a $v$, vytvoříme kódové slovo méně pravděpodobné hodnoty připojením symbolu $1$ za kódové slovo $C(x)$ a analogicky kódové slovo více pravděpodobné hodnoty připojením symbolu $0$ za $C(x)$