9. Markovské řetězce se spojitým časem. Souvislost s Markovskými řetězci s diskrétním časem a s Poissonovým procesem. (NI-VSM)

---

Markovské řetězce se spojitým časem

Important

• Náhodný proces $\{X_n | n ∈ N_0\}$ s nejvýše spočetnou množinou stavů $S$ nazýváme markovský řetězec s spojitým časem, pokud splňuje markovskou podmínku, tj. pokud $∀k ∈ \mathbb{N}$, a $∀0, t_0, . . . , t_{k} ∈ \mathbb{R}_0^+$ a $∀s_0, . . . , s_k ∈ S$platí: $$P(X_{t_k}=s_k|X_{t_{k-1}}=s_ {k-1},...,X_{t_0}=s_0) = P(X_{t_k}=s_k|X_{t_{k-1}}=s_{k-1})$$
  • Rozdělení v čase $t ∈ [0, +∞)$: Pro $i ∈ S$: $$p_i(t) := P(X_t = i) ,\quad\quad p(t) := (p_1(t), p_2(t), . . .)$$
• Matice pravděpodobností přechodu za čas mezi $s$ a $t ≤ s$: $$P_{ij} (t, s) := P(X_s = j|X_t = i) , \quad \quad P(t, s) := (P_{ij} (t, s))_{i,j∈S}$$
• Náhodný proces $\{X_t | t ≥ 0\}$ s nejvýše spočetnou množinou stavů $S$ je markovský právě tehdy když $∀k ∈ \mathbb{N}$, a $∀0, t_0, . . . , t_{k} ∈ \mathbb{R}_0^+$ a $∀s_0, . . . , s_k ∈ S$ platí: $$P(X_{t_0} = s_0,..., X_{t_k} = s_k) = p_{s_0} (t0) · P_{s_0s_1} (t_0, t_1)\cdot\cdot\cdot P_{s_{k−1}s_k} (t_{k−1}, t_k)$$

• Chapman-Kolmogorova rovnice
  • Jedna se o vetu která říká ze pravděpodobnost přechodu z $n$ do $r$ je stejná jako pravděpodobnost přechodu z $n$ do $m$ a pak $m$ do $r$ pokud $t\leq s \leq r \in [0,+\infty)$
  • $P(t,r) = P(t,s)\cdot P(s,r)$

Homogenní markovský řetězec

Important

• Markovský řetězec je homogenní pokud přechod z $t$ do $s$ je stejný jako z $0$ do $s$.
• To znamená ze nezaleží na aktuálním casu. Matice přechodu je furt stejná
• Markovský řetězec $\{X_t | t ≥ 0\}$ je homogenní, pokud $∀t, s ≥ 0$ platí: $$P(t,t+s) = P(0,s) := P(s)$$
• Chapman-Kolmogorova rovnice
• Pokud je markovský řetězec homogenní pak ma rovnice tvar: $P(t+s) = P(t)\cdot P(s)$
• Rozdělení v čase $t ≥ 0$ je pak dáno jako: $$p(t) = p(0)P(t)$$

Matice skokových intenzi

Important

• Matice skokových intenzit musíme vypočítat pomoci derivace. Kde vlastně hledáme nekonečně malý krok tedy limitně se blížíme k $0$ zprava
• Matice skokových intenzit je definovaná jako $Q = (Q_{ij} )_{i,j∈S}$: $$Q:=\lim_{h\rightarrow+0}\frac{1}{h}(P(h)-I)$$
• Pokud limity existuji můžeme $Q$ vlastně vypočítat pomoci derivace: $$Q = P'(0)$$
• Vlastnosti:
• Součet v řádku je $0$ tedy cely řádek bez diagonálního prvku je $a$ a pak diagonální prvek je $-a$
• Na diagonále je záporné číslo. Udává jak moc intenzivně se chceme z aktuálního stavu dostat ven.

Stacionární rozdělení

Important

• Jedna se o vektor s počátečním stavem ze kterého už se nedostanu.
• Toto rozděleni popisuje dlouhodobé chovaní celého Markovského řetězce
• Jou-li všechny stavy přechodné nebo trvalé nulové, stacionární rozdělení neexistuje
• Jsou-li všechny stavy trvalé nenulové, stacionární rozdělení $π$ existuje a je jediné.
• Může byt vice stacionárních rozdělení
• Buď $\{X_t|t \geq 0\}$ markovský řetězec s pravděpodobnostmi přechodu $P(t)$ pak vektor $\pi$ je stacionárním rozdělením pokud platí pro všechna $t\geq 0$:
• $\pi\cdot P(t)=\pi$
• Vektor $π$ je stacionárním rozdělením, právě tehdy, když splňuje
• $\pi Q = 0$

Kolmogorovy rovnice

• Máme matici skokových intenzit a chceme zjistit matice přechodu. Na to slouží Kolmogorovy rovnice: $P'(t)=QP(t)$ a $P'(t)=P(t)Q$

Poissonový process

Čítací process

• Jedna se o process který jde vždy "nahoru" .
• To znamená ze trajektorie je nezáporná, celočíselná a neklesající
  • $N_t\geq 0$
  • $N_t \in \mathbb{Z}$
  • $i\leq j \Longleftrightarrow N_i\leq N_j$

Poissonový process

• Jedna se o náhodný čítací proces s nezávislými exponenciálně rozdělenými časy mezi událostmi.

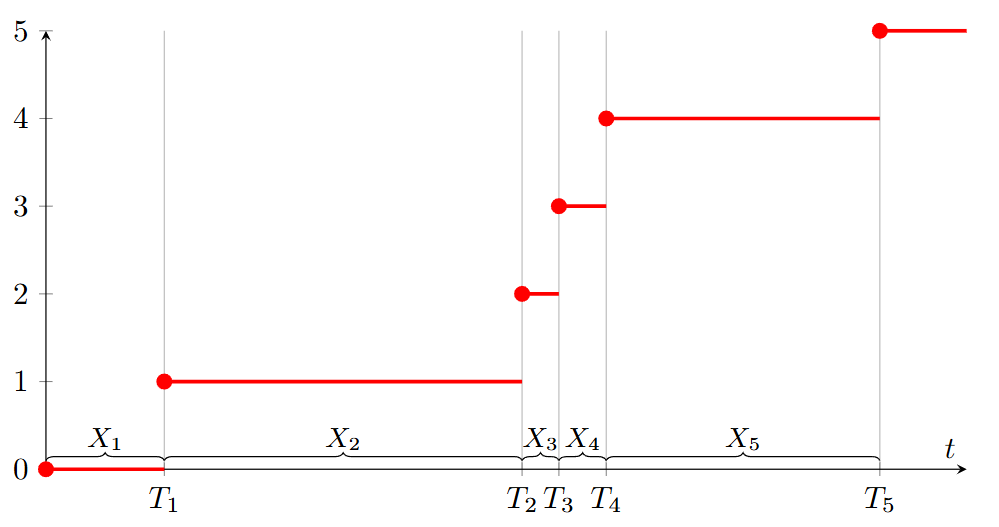
• Bud $\{X_j|j\in\mathbb{N}\}$ nezávislý stejně rozdělený process s exponenciálním rozdělením: $\text{Exp}(\alpha)$
  • První definujeme kolik casu je potřeba do příchodu $n$-té události jako tedy náhodný process $\{T_n|n\in \mathbb{N}\}$: $$T_0=0\quad\quad T_n=T_{n-1}+X_n=\sum_{j=1}^nX_j\quad n\geq 1$$
  • Poté můžeme definovat Poissonův process jako $\{N_t|t \in [0+\infty)\}$: $$N_t(\omega) = \max\{n\in\mathbb{N}|T_n(\omega)\leq t\}$$

Souvislosti

Markovské řetězce s diskrétním casem a s Poissonovým process

• Poissonový process je jedním z přikladu markovského řetězce se spojitým časem.
• Matice skokových intenzit pak vypadá takto: $$Q = \begin{bmatrix} -\lambda & \lambda & 0 & 0 & \cdots \\ 0 & -\lambda & \lambda & 0 & \cdots \\ 0 & 0 & -\lambda & \lambda & \cdots \\ \vdots & \vdots & \vdots & \vdots & \vdots & \ddots \end{bmatrix}$$
• Bezpaměťovost – Oba procesy jsou bezpaměťové tedy: Pokud přijdu k procesu v čase $t$, tak je to stejné, jako kdyby se systém restartoval, tzn. můžu začít kdekoliv, ale rozdělení se nezmění
• Diskrétní řetězec: $D=I+\frac{1}{\alpha}Q$