17. QR rozklad: metody výpočtu, použití při výpočtu odhadu metodou nejmenších čtverců, QR algoritmus pro hledání vlastních čísel. (NI-PON)

---

QR rozklad

QR rozklad převádí matici $A \in \mathbb{R}^{m \times n}$ na součin dvou matic: ortogonální matice $Q$ a horní trojúhelníkové matice $R$.

Matematická formulace QR rozkladu

$$A = QR$$

kde: - $Q \in \mathbb{R}^{m \times m}$ (ortogonální nebo unitární, pokud má komplexní prvky), - $R \in \mathbb{R}^{m \times n}$ (horní trojúhelníková).

QR rozklad lze chápat jako faktorizaci matice $A$ do součinu $QR$:

1. Ortogonalita matice $Q$: Sloupce matice $Q$ jsou ortonormální ("kolmé na sebe"), tedy $Q^\top Q = I$, kde $I$ je jednotková matice.
2. Horní trojúhelníková matice $R$: Matice $R$ má nenulové prvky pouze na diagonále a nad ní.

Pro každou matici $A \in \mathbb{R}^{m \times n}$ (s $m \geq n$) existuje QR rozklad.

Metody výpočtu QR rozkladu

Givensovy rotace

Givensova rotace je ortogonální matice, která otáčí dvojici řádků matice tak, aby byl jeden prvek vynulován. Například chceme vynulovat prvek $b$ v dvojici $[a, b]$. Givensova rotace zajistí, že nová dvojice je: $$\begin{bmatrix} r \\ 0 \end{bmatrix},$$ kde $r$ je délka (norma) původního vektoru: $$r = \sqrt{a^2 + b^2}.$$

Intuitivní odvozování $\alpha$ a $\beta$

Parametry Givensovy rotace, označené jako $\alpha$ a $\beta$, určují, jakým způsobem se dvojice $[a, b]$ „otočí“, aby byla jedna složka ($b$) nulová. Tyto parametry jsou definovány jako: $$\alpha = \frac{a}{\sqrt{a^2 + b^2}}, \quad \beta = \frac{b}{\sqrt{a^2 + b^2}}.$$

Intuitivně si to lze představit jako proces normalizace vektoru $[a, b]$ tak, aby $\alpha$ představovalo „projekci“ na osu $a$ (původní prvek, který chceme zachovat), a $\beta$ odpovídalo „projekci“ na osu $b$ (prvek, který chceme vynulovat). Poměr $\frac{a}{r}$ a $\frac{b}{r}$ tedy určuje, jaké „váhy“ použijeme při kombinaci prvků tak, aby výsledek měl správnou délku $r$ a jeden člen byl nulový. viz:

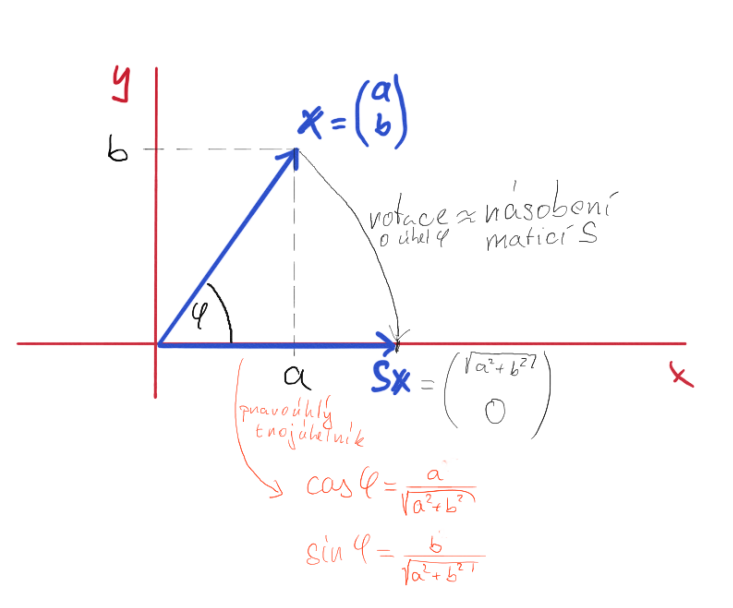
Givensova rotace $G_{(i,j)}$

Givensova rotace $G_{(i,j)}$ je jednotková matice s modifikacemi pouze na pozicích odpovídajících řádkům $i$ a $j$. Její obecný tvar je:

$$G_{(i,j)} = \begin{bmatrix} 1 & 0& & \cdots & & & 0 & & \\ 0 & \ddots & & & & & & & \\ & & \alpha & 0 & \cdots & & \beta & & \\ & & 0 & \ddots & & & 0 & & \\ \vdots & & \vdots & & 1 & & \vdots & & \\ & & & & & \ddots & & & \\ & &-\beta & 0 & \cdots & & \alpha & & \\ & & & & & & & \ddots & \\ 0 & & & & & & & & 1 \end{bmatrix}.$$

Při násobení matice $A$ zleva Givensovou rotací $G_{(i,j)}$ dochází ke změně pouze ve dvou řádcích ($i$ a $j$); ostatní řádky zůstávají nedotčené .

Algoritmus

1. Inicializace:

   • Nastav $Q$ jako jednotkovou matici $I \in \mathbb{R}^{m \times m}$.
   • Pracuj s kopií matice $A$, která bude transformována na $R$.

2. Iterace přes všechny sloupce matice $A$:

   • Pro sloupec $j$ eliminuj všechny prvky $a_{ij}$ pod diagonálou ($i > j$).

3. Pro každý prvek $a_{ij}$ ($i > j$):

   • Výpočet normy: $$r = \sqrt{a_{jj}^2 + a_{ij}^2}.$$
   • Výpočet parametrů Givensovy rotace: $$\alpha = \frac{a_{jj}}{r}, \quad \beta = \frac{a_{ij}}{r}.$$
   • Vytvoření Givensovy rotace $G_{(j,i)}$:
     • Modifikuj řádky $j$ a $i$ s parametry $\alpha$ a $\beta$:
     • Na diagonálních pozicích $j,j$ a $i,i$: $\alpha$,
     • Na pozicích $j,i$ a $i,j$: $\beta$ a $-\beta$.
   • Aplikace rotace:
     • Zaktualizuj matici $A$: $A \leftarrow G_{(j,i)} A$ (vynuluj $a_{ij}$).
     • Zaktualizuj matici $Q$: $Q \leftarrow Q G_{(j,i)}^\top$.

4. Opakuj pro všechny sloupce $j$:

   • Pokračuj, dokud nejsou všechny prvky pod diagonálou vynulovány.

5. Výstup:

   • Matice $A$ je nyní horní trojúhelníková matice $R$.
   • Matice $Q$ je ortogonální a odpovídá součinu všech Givensových rotací.

Householderovy reflexe

Householderovy reflexe jsou ortogonální transformace, které zrcadlí vektory vzhledem k hyperrovině procházející počátkem souřadnic. Tato metoda se používá k vynulování všech složek vektoru mimo první, což umožňuje postupně převést matici na horní trojúhelníkový tvar.

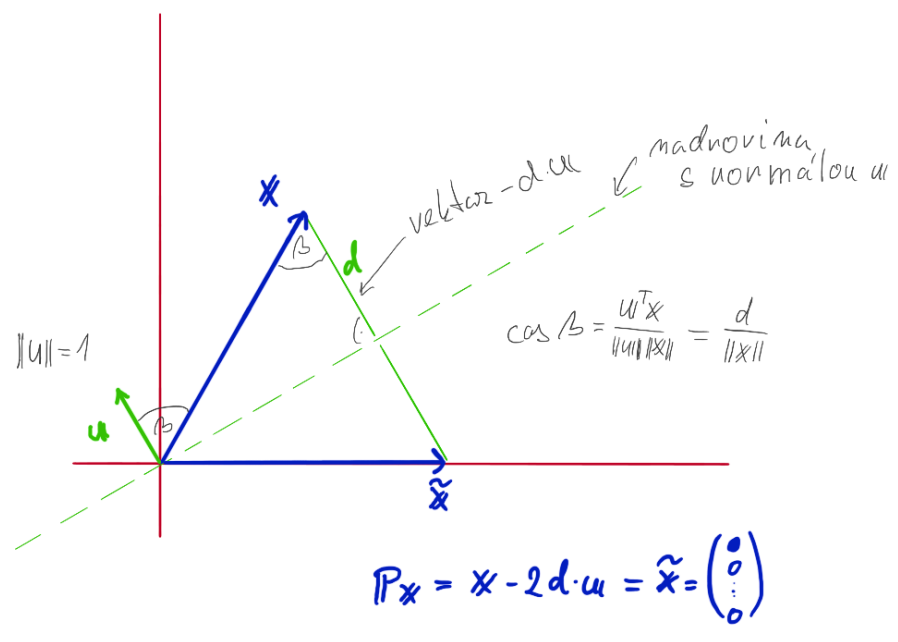
Princip reflexe

Reflexe nastavuje „zrcadlo“ ve formě nadroviny, která je definována normálovým jednotkovým vektorem $\mathbf{u}$. Každý vektor $\mathbf{x}$, který chceme zrcadlit, bude transformován na svůj odraz $\tilde{\mathbf{x}}$ pomocí matice reflexe $P$ takto:

$$P\mathbf{x} = \tilde{\mathbf{x}}= \begin{bmatrix} \pm \|\mathbf{x}\| \\ 0 \\ \vdots \\ 0 \end{bmatrix}.$$

Norma $\|\mathbf{x}\|$ je délka vektoru $\mathbf{x}$, přičemž první složka výsledného odrazu je rovna normě vektoru (se znaménkem závislým na výběru).

Matice reflexe $P$ má tvar:

$$P = I - 2\mathbf{u}\mathbf{u}^\top$$

kde:

• $I$ je jednotková matice,
• $\mathbf{u}$ je normálový jednotkový vektor hyperroviny (tj. $\|\mathbf{u}\| = 1$).

Zjištění $P$

Zrcadlení vektoru $\mathbf{x}$ provádíme vůči hyperrovině, která je definovaná jednotkovým normálovým vektorem $\mathbf{u}$. Tento normálový vektor $\mathbf{u}$ určuje, kde se nachází „zrcadlo“, vůči kterému zrcadlíme.

Proces reflexe zahrnuje následující kroky:

1. Najdeme projekci vektoru $\mathbf{x}$ na normálový vektor $\mathbf{u}$: $$\mathbf{d} = (\mathbf{u}^\top \mathbf{x}) \mathbf{u}$$

   • Tato projekce odpovídá kolmé vzdálenosti vektoru $\mathbf{x}$ od hyperroviny.
   • Skalární součin $u^Tx$ udává délku komponenty $x$ ve směru $u$.
   • Vynásobením této délky směrovým vektorem $u$ získáme požadovaný projekční vektor $d$.

2. Vektor $\mathbf{x}_{\text{na nadrovině}}$, který leží na hyperrovině, získáme tak, že projekci $\mathbf{d}$ odečteme od $\mathbf{x}$: $$\mathbf{x}_{\text{na nadrovině}} = \mathbf{x} - \mathbf{d}$$

3. Zrcadlový obraz $\tilde{\mathbf{x}}$ vznikne posunutím vektoru $\mathbf{x}$ o dvojnásobek projekce na druhou stranu „zrcadla“: $$\tilde{\mathbf{x}} = \mathbf{x} - 2\mathbf{d}$$ Po dosazení $\mathbf{d} = (\mathbf{u}^\top \mathbf{x}) \mathbf{u}$ dostáváme. $$\tilde{\mathbf{x}} = \mathbf{x} - 2(\mathbf{u}^\top \mathbf{x}) \mathbf{u}$$ Tento vztah násobení maticí nám říká, že matici $P$ můžeme zapsat jako: $$P = I - 2\mathbf{u}\mathbf{u}^\top$$

Konstrukce Householderova vektoru $\mathbf{u}$

Abychom zkonstruovali matici $P$, potřebujeme vektor $\mathbf{u}$. Postup je následující:

1. Definice vektoru $\mathbf{x}$:

   • $\mathbf{x}$ je sloupec matice $A$, který zpracováváme (včetně prvků pod diagonálou, které chceme eliminovat).

2. Určení cílového vektoru:

   • Cílový odraz $\tilde{\mathbf{x}}$ má tvar: $$\tilde{\mathbf{x}} = \begin{bmatrix} \pm \|\mathbf{x}\| \\ 0 \\ \vdots \\ 0 \end{bmatrix}$$
   • Znaménko složky $\pm \|\mathbf{x}\|$ volíme tak, aby se minimalizovala numerická chyba: $\pm \|\mathbf{x}\|$ má opačné znaménko než $x_1$.

3. Výpočet vektoru $\mathbf{u}$: $$\mathbf{u} = \frac{\mathbf{x} - \tilde{\mathbf{x}}}{\|\mathbf{x} - \tilde{\mathbf{x}}\|}$$

4. Nyní máme jednotkový vektor $\mathbf{u}$, který definuje nadrovinu reflexe.

Algoritmus

1. Inicializace:

   • Nastav $Q$ jako jednotkovou matici $I \in \mathbb{R}^{m \times m}$.
   • Pracuj s kopií matice $A$, která bude transformována na $R$.

2. Iterace přes sloupce matice $A$:

   • Pro sloupec $j$ eliminuj všechny prvky $a_{ij}$ pod diagonálou ($i > j$).

3. Pro každý sloupec $j$:

   • Definuj podvektor $\mathbf{x}$:
     • $\mathbf{x}$ je sloupcový vektor tvořený prvky od $a_{jj}$ až po $a_{mj}$.
   • Urči cílový vektor $\tilde{\mathbf{x}}$:
     • $\tilde{\mathbf{x}} = [\pm \|\mathbf{x}\|, 0, \dots, 0]^\top$, kde znaménko $\pm$ je opačné než u $x_1$.
   • Spočítej Householderův vektor $\mathbf{u}$: $$\mathbf{u} = \frac{\mathbf{x} - \tilde{\mathbf{x}}}{\|\mathbf{x} - \tilde{\mathbf{x}}\|}$$
   • Vytvoř matici $P_j$: $$P_j = I - 2\mathbf{u}\mathbf{u}^\top$$
   • Aplikace reflexe:
     • Zaktualizuj matici $A$: $A \leftarrow P_j A$.
     • Zaktualizuj matici $Q$: $Q \leftarrow Q P_j^\top$.

4. Pokračuj na další sloupec:

   • Opakuj kroky 3.1 až 3.4 pro všechny sloupce $j$.

5. Výstup:

   • Matice $A$ je nyní horní trojúhelníková matice $R$.
   • Matice $Q$ je ortogonální a odpovídá součinu všech Householderových matic.

Použití QR při OLS

Při hledání vektoru $w$, který minimalizuje normu reziduí $\|Xw - Y\|^2$, můžeme využít QR rozklad matice $X$.

Hlavní myšlenka

1. Použitím QR rozkladu minimalizovanou normu přepíšeme: $$\|Xw - Y\|^2 = \|QRw - Y\|^2.$$
2. Využitím ortogonality $Q$ platí: $$\|QRw - Y\|^2 = \|Q^\top(QRw - Y)\|^2 = \|Q^\top Y - Q^\top QRw\|^2 = \|Q^\top Y - Rw\|^2$$
3. Rozepišme $R$ a $Q^\top Y$ explicitně: $$R = \begin{bmatrix} R_S \\ \theta \end{bmatrix}, \quad Q^\top Y = \begin{bmatrix} Q_L^\top Y \\ Q_R^\top Y \end{bmatrix}$$
4. Po dosazení dostáváme: $$\|Q^\top Y - Rw\|^2 = \left\| \begin{pmatrix} R_S w \\ \theta \end{pmatrix} - \begin{pmatrix} Q_L^\top Y \\ Q_R^\top Y \end{pmatrix} \right\|^2$$
5. Norma se tedy rozkládá na dvě části: $$\|Q^\top Y - Rw\|^2 = \left\| \begin{pmatrix} R_S w - Q_L^\top Y \\ - Q_R^\top Y \end{pmatrix}= \right\|^2 = \|R_S w - Q_L^\top Y\|^2 + \|Q_R^\top Y\|^2$$
6. Protože druhý člen $\|Q_R^\top Y\|^2$ nezávisí na $w$, minimalizace závisí pouze na prvním členě: $$\min_w \|Xw - Y\|_2^2 = \min_w \|R_S w - Q_L^\top Y\|_2^2.$$

Výhody použití QR rozkladu

1. Numerická stabilita:

   • Ortogonalita matice $Q$ zaručuje, že transformace nezesilují chyby.
   • Horní trojúhelníková struktura matice $R_S$ umožňuje efektivní řešení.

2. Efektivní výpočet:

   • QR rozklad lze implementovat s časovou složitostí $O(mn^2)$.

3. Řešení pro případy s přeurčenými systémy:

   • QR metoda je dobře definovaná i pro přeurčené systémy ($m > n$) a poskytuje odhad minimální normy.

QR algoritmus pro hledání vlastních čísel

QR algoritmus je numerická metoda pro nalezení vlastních čísel čtvercové matice $A \in \mathbb{R}^{n \times n}$. Metoda iterativně využívá QR rozklad pro transformaci matice $A_0$ na posloupnost podobných matic, která konverguje k horní trojúhelníkové matici. Diagonální prvky této výsledné matice odpovídají vlastním číslům původní matice.

Definice

• Vlastní číslo: Vlastní číslo $\lambda$ je číslo, které popisuje, jakým způsobem matice $A$ ovlivňuje určitý směr v prostoru. Existuje vektor $\mathbf{v}$ (tzv. vlastní vektor), který při násobení maticí $A$ zůstává po směru zachován (může změnit délku), tj. platí: $$A \mathbf{v} = \lambda \mathbf{v}$$
• Podobné matice: Matice $A$ a $B$ jsou podobné, pokud existuje regulární matice $P$ taková, že: $$B = P^{-1}AP$$ Podobné matice mají stejná vlastní čísla, protože zachovávají charakteristický polynom.
• Horní trojúhelníková matice: Matice, která má nenulové prvky pouze na diagonále a nad ní. Tato matice má vlastní čísla rovná svým diagonálním prvkům.
• Matice $A$ je podobna matici $RQ$: $\Rightarrow A=QR \Rightarrow R=Q^\top A \Rightarrow RQ = Q^\top A Q$

Algoritmus

1. Inicializace:

   • Začneme s maticí $A_0 = A$.

2. Iterace:

   • Pro každou iteraci $k$:
     1. Najdeme QR rozklad: $$A_k = Q_k R_k$$ kde $Q_k$ je ortogonální matice a $R_k$ je horní trojúhelníková matice.
     2. Vypočítáme novou podobnou matici: $$A_{k+1} = R_k Q_k$$
3. Konvergence:
   • Iterace často konverguje k horní trojúhelníkové matici $T$: $$A_k \to T, \quad T = \begin{bmatrix} \lambda_1 & * & \cdots & * \\ 0 & \lambda_2 & \cdots & * \\ \vdots & \vdots & \ddots & * \\ 0 & 0 & \cdots & \lambda_n \end{bmatrix}$$ Diagonální prvky $T$ jsou vlastní čísla původní matice $A$.

Výhody algoritmu

1. Numerická stabilita:
   • Ortogonální matice $Q_k$ zachovávají normy.
2. Efektivita:
   • S Hessenbergovou formou se sníží výpočetní složitost.
3. Schopnost nalézt všechna vlastní čísla:
   • Na rozdíl od metod jako mocninná metoda, která hledá pouze dominantní vlastní číslo.