2. Splňování omezení s konečnými doménami (CSP), pokročilé prohledávání (backjumping, dynamický backtracking), filtrace domén a lokální konzistenční techniky, globální omezení, rozhodovací heuristiky. (NI-UMI)

---

CSP

• Problem splňovaní omezeni
• Máme problem který dokážeme vyjádřit pomoci proměnných. A máme podmínky které omezuji jake výsledky mohou byt v proměnných
• Jedna se o trojici: $\text{CSP}=(X,D,C)$
  • $X$ - konečná množina proměnných
    • určují co můžeme rozhodnout
  • $D$ - konečný obor hodnot pro proměnné
    • jaké máme při rozhodování možnosti
  • $C$ - konečná množina podmínek nad $X$
    • určují omezení při rozhodování
• Cil je vyplnění proměnných tak abychom splnily všechny omezení
• Obvyklí postup v CSP:
  1. Filtrace
     • Odebereme všechny možné stavy které na první krok jsou vyloučeny podmínkami
  2. Definitivní zvoleni
     • Tam kde se nám vyfiltruje vše až na jednu podmínku tak to vybereme.
  3. Postupné vnořovaní
     • Když už nemáme definitivní zvoleni tak postupně zkoušíme dosadit možné proměnné a opakujeme od bodu 1.
     • Tedy postupně prohledáváme stavový prostor možností
• Výhody CSP
  • Obecné prohledávací techniky
    • Můžeme používat standartní techniky např. BFS, DFS v prohledávaní
  • Heuristiky
    • Používají se obecné heuristiky které nezávisí na úloze

Prohledávání

Základní pojmy

• Částečné přiřazení: $S'$ - Misto celého stavového prostoru pro danou proměnu zúžíme její vyhodnoceni na podmnožinu možných stavů
  • Pracovní doména: Set možných hodnot které dokážeme přiradit konkrétní proměnné
• Konzistentní stav: Přiřazené hodnoty neporušují podmínky
• Počáteční stav: Prázdné přiražení
• Akce: Přiřazení hodnoty proměnné z její domény
• Cílový stav: Všechny proměnné jsou ohodnoceny a navíc stav je konzistentní

Rozhodovací heuristiky

Potřebujeme najit system vybíraní hodnot tak abych co nejrychleji došli k řešení. Jsou dvě věci na které koukáme. Jaké proměnné budeme ohodnocovat a jakou hodnotu zvolíme pro ohodnoceni.

• Proměnné
  • Výběr nejvíce omezené proměnné
    • Ohodnocujeme proměnnou, v jejíž pracovní doméně je nejméně hodnot
  • Výběr „klíčové“ proměnné
    • Ohodnocujeme proměnnou, která je součástí nejvíce podmínek
• Hodnoty
  • Hodnota s nejmenším dopadem
    • Vybíráme hodnoty tak abychom co nejméně omezovali pracovní domény zbylých proměnných

Filtrace domén

• Dopředná kontrola
  • Standartní algoritmus v postupném vnořovaní nefiltruje moznosti. Proto tato kontrola, při každém ohodnocení proměnné kontrolujeme související podmínky.
  • Kontrolujeme pouze ohodnocené podmínky.
• Důrazná dopředná kontrola
  • Kontrolujeme i částečně ohodnocené podmínky
  • Například: Ohodnotili jsme $X_1 = 0$ a $X_2 = 0$. Z toho nám vypadlo ze $X_3$ může mít hodnoty pouze $X_3 \subset \{2\}$ . I když jsme tedy neohodnotili $X_3 = 2$ tak už to tak bereme a kontrolujeme podmínky s tím ze $X_3 = 2$
    • V tomto přiklade neberte co znamená $X_{1,2,3}$ ani jaká je množina podmínek.
• Hranová konzistence
  • Kontroluje konzistenci mezi všemi dvojicemi proměnných
  • Pro každou hodnotu v doméně jedné proměnné musí existovat alespoň jedna přípustná hodnota v doméně druhé proměnné
  • Používá algoritmus AC-3:
    1. Vytvoří frontu všech hran (dvojic proměnných)
    2. Postupně odebírá hrany z fronty a kontroluje konzistenci
    3. Při změně domény přidá zpět do fronty všechny ovlivněné hrany
    4. Končí, když je fronta prázdná
  • Oproti dopředné kontrole je důkladnější, ale výpočetně náročnější
  • Může odhalit nekonzistence, které dopředná kontrola nenajde

Globální omezení

Globální omezení jsou speciální podmínky, které pracují s více proměnnými najednou a mají efektivní filtrační algoritmy.

Zobecněná hranová konzistence (GAC)

Princip: - Pro podmínku $c$ nad proměnnými $x_1,x_2,...,x_k$: - Pro každou hodnotu $d_1 \in D(x_1)$ hledáme podpory $d_2 \in D(x_2),...,d_k \in D(x_k)$ - Musí platit $(d_1,d_2,...,d_k) \in c$ - Pokud podpora neexistuje, hodnota $d_1$ se odstraní z $D(x_1)$

Příklad: All-Different - Vyžaduje různé hodnoty pro všechny proměnné - Implementace: 1. Vytvoření bipartitního grafu 2. Hledání maximálního párování 3. Odstranění hran mimo maximální párování

Symetrie

Princip: - Identifikace a eliminace symetrických řešení - Přidání podmínek pro rozbití symetrií - Redukce prohledávacího prostoru

Příklad: N-královen - Proměnné: $q_1,q_2,...,q_N \in \{1,2,...,N\}$ - Typy symetrií: - Rotace o 90°, 180°, 270° - Překlopení podle úhlopříčky - Překlopení podle horizontály - Řešení: - Přidání lexikografického uspořádání: - $(q_1,q_2,...,q_N) \leq_{lex} (\pi(q_1), \pi(q_2),..., \pi(q_N))$ - kde $\pi$ je permutace odpovídající symetrii - Výhoda: Zachování pouze jednoho reprezentanta z každé třídy symetrických řešení

Prohledávací algoritmy

Chronologicky backtracking

• Rekurzivní prohledávání do hloubky (DFS)
  • Postupně ohodnocuje proměnné
  • Narazime-li na proměnou kterou nedokážeme ohodnotit vracíme se zpět a vybíráme jiné ohodnoceni
  • Algoritmus můžeme vylepšit různými filtračními technikami
  • Nevýhody
    • Čeká na ohodnocení všech proměnných podmínky, pak kontroluje její platnost
      • Pouze pokud nevyužijeme nějaké filtrační techniky
    • Nalezené konflikty zapomíná a objevuje znovu.
      • DFS může vyzkoušet stejné moznosti vícekrát s jinými počátečními hodnotami. Kde počáteční hodnoty neovlivňuji konflikty které se stanou níž ve vyhledávacím stromu

Backjumping

• Vylepšení chronologického backtrackingu
• Při nalezení konfliktu se nevrací jen o jednu úroveň, ale skočí zpět k proměnné, která konflikt způsobila
• Žádná filtrace zde neprobíhá
• Conflict-directed backjumping
  • Pro každou proměnnou $x$ a její hodnotu $d$ si udržuje konfliktní množinu $\text{Conf}_d$
    • Obsahuje proměnné, které způsobily, že nešlo použít hodnotu $d$
  • Když selže přiřazení hodnoty $d$ proměnné $x$:
    1. Do $Conf_d$ se uloží proměnné, které způsobily konflikt
    2. Zkusí se další hodnota z domény $D(x)$
  • Když selžou všechny hodnoty z domény $D(x)$:
    1. Vytvoří celkovou konfliktní množinu $\text{Conf}$ jako sjednocení všech $\text{Conf}_d$
    2. Odstraní z ní proměnnou $x$ ($\text{Conf} \setminus \{x\}$)
    3. Skočí zpět k poslední proměnné z výsledné konfliktní množiny
  • Výhody:
    • Efektivnější návrat při nalezení konfliktu
    • Vyhýbá se zbytečnému prohledávání stavového prostoru
    • Lépe využívá informace o struktuře problému díky sledování konfliktních množin
  • Nevýhody:
    • Nalezené konflikty zapomíná a objevuje znovu.
  • Příklad:

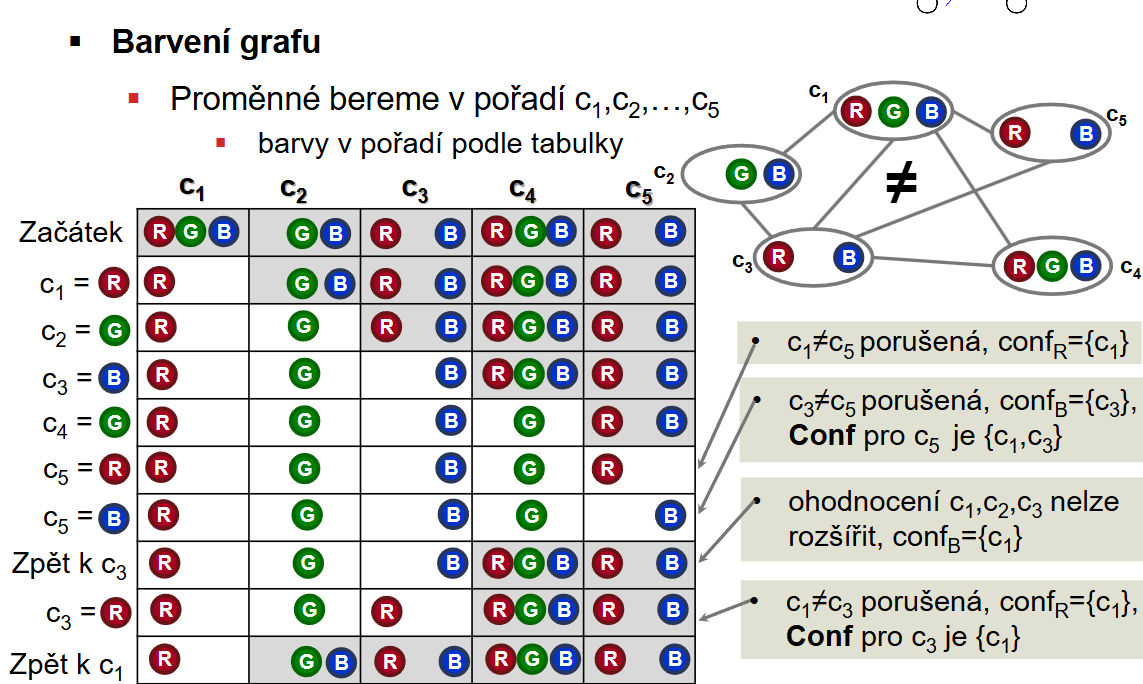
Dynamický backtracking

• Další vylepšení backtrackingu
• Hlavní vylepšení:
  1. Zachovává část správného ohodnocení při návratu
  2. Umožňuje měnit pořadí proměnných během řešení
• Práce s nogoody:
  • Nogoody slouží k:
    • Zaznamenání prohledaného prostoru
    • Udržování aktuálního částečného přiřazení
  • Pro každou proměnnou $x$ udržuje eliminační vysvětlení (nogoody) pro vyřazené hodnoty $y_1 \neq S'(y_1) \vee ... y_k \neq S'(y_k)$
  • Specifické nogoody lze skládat do obecnějších nogoodu
    • Po složeni se specifické nogoody můžou zapomenout
• Výhody:
  • Umožňuje dynamické přeuspořádání proměnných během řešení
• Nevýhody:
  • Složitější implementace než u předchozích metod
  • Nutnost správy nogoodů při změně pořadí proměnných