3. Systematické a lokální splňování v logice (DPLL, CDCL, WalkSAT, posílání zpráv). Automatické uvažování, rozhodování v teoriích prvního řádu, obecná rezoluce, princip SAT-modulovaných teorií (SMT). Zpracování přirozeného jazyka. (NI-UMI)

---

Výroková logika

Výroková logika je základní formální systém pro reprezentaci a manipulaci s logickými výroky. Pracuje s atomickými výroky, které mohou být buď pravdivé nebo nepravdivé, a logickými spojkami (AND, OR, NOT, ...).

Výroková formule je:

• Atomický výrok (proměnná): $p, q, r, ...$

• Složený výrok vytvořený pomocí logických spojek:

  • Negace (NOT): $\neg p$
  • Konjunkce (AND): $p \wedge q$
  • Disjunkce (OR): $p \vee q$
  • Implikace: $p \rightarrow q$
  • Ekvivalence: $p \leftrightarrow q$

Konjunktivní normální forma (CNF):

• Standardní forma pro reprezentaci výrokových formulí
• Konjunkce disjunkcí literálů: $(l_{11} \vee ... \vee l_{1n}) \wedge ... \wedge (l_{m1} \vee ... \vee l_{mk})$
• Literál je proměnná nebo její negace
• Většina algoritmů pro řešení splnitelnosti pracuje s formulemi v CNF

Splňování formulí

Problém splnitelnosti (SAT) je úloha nalezení ohodnocení proměnných výrokové formule tak, aby byla formule pravdivá. Pro formule v CNF to znamená nalézt takové přiřazení hodnot proměnným, aby byla pravdivá alespoň jedna proměnná v každé klauzuli.

Probíraly jsme systematické (DPLL, CDCL) které vždy najdou výsledek a lokální které využívají náhodné změny k řešení problému. Lokální algoritmy nemusí vždy najit výsledek

DPLL (Davis-Putnam-Logemann-Loveland)

Základní algoritmus pro systematické řešení SAT problému, který rozšiřuje backtracking o dvě klíčové techniky:

Jednotková propagace (Unit Propagation):

• Pokud klauzule obsahuje jediný neohodnocený literál, musí být tento literál pravdivý
• Aplikuje se rekurzivně
• Příklad: $(¬u ∨ w) ∧ (u ∨ v) ∧ (u) ∧ (¬w ∨ z)$
  1. Jednotková klauzule $u=1$
  2. Protože máme rozhodnuto o $u$ můžeme rozhodnout o $w=1$
  3. Protože máme rozhodnuto o $u,w$ můžeme rozhodnout o $z=1$

Propagace čistých literálů (Pure Literal Elimination):

• Literál je čistý, pokud se vyskytuje buď pouze jako pozitivní, nebo pouze jako negativní literál
• Čistý literál můžeme bezpečně nastavit na hodnotu, která jej splní
• Příklad: Ve formuli $(x \vee y) \wedge (x \vee \neg z) \wedge (\neg y \vee z)$ je $x$ čistý literál

Algoritmus:

1. Aplikuj jednotkovou propagaci a propagaci čistých literálů
2. Pokud je formule prázdná, vrať SUCCESS
3. Pokud obsahuje prázdnou klauzuli, vrať FAILURE
4. Vyber proměnnou a rekurzivně zkus obě hodnoty
5. Pokud obě větve selžou, vrať FAILURE

Výhody:

• Kompletní algoritmus (najde řešení, pokud existuje)
• Efektivnější než čistý backtracking díky propagačním technikám

CDCL (Conflict-Driven Clause Learning)

Moderní vylepšení DPLL algoritmu, které se učí z konfliktů během prohledávání.

Analýza konfliktu:

• Využívá předchůdcovské klauzule (antecedent clause)
  • Pro literál $l$ ohodnocený jednotkovou propagací je to klauzule, kde byl $l$ poslední neohodnocený
• Vytváří implikační graf $G = (Var(\phi) \cup K, E)$:
  • Vrcholy jsou proměnné a speciální konfliktní vrchol $K$
  • Hrany $(x_i,y)$ ukazují, že $y$ byla ohodnocena jednotkovou propagací kvůli ohodnocení $x_1,x_2,...,x_k$
  • Vrcholy obsahují informaci o rozhodovací úrovni ohodnocení
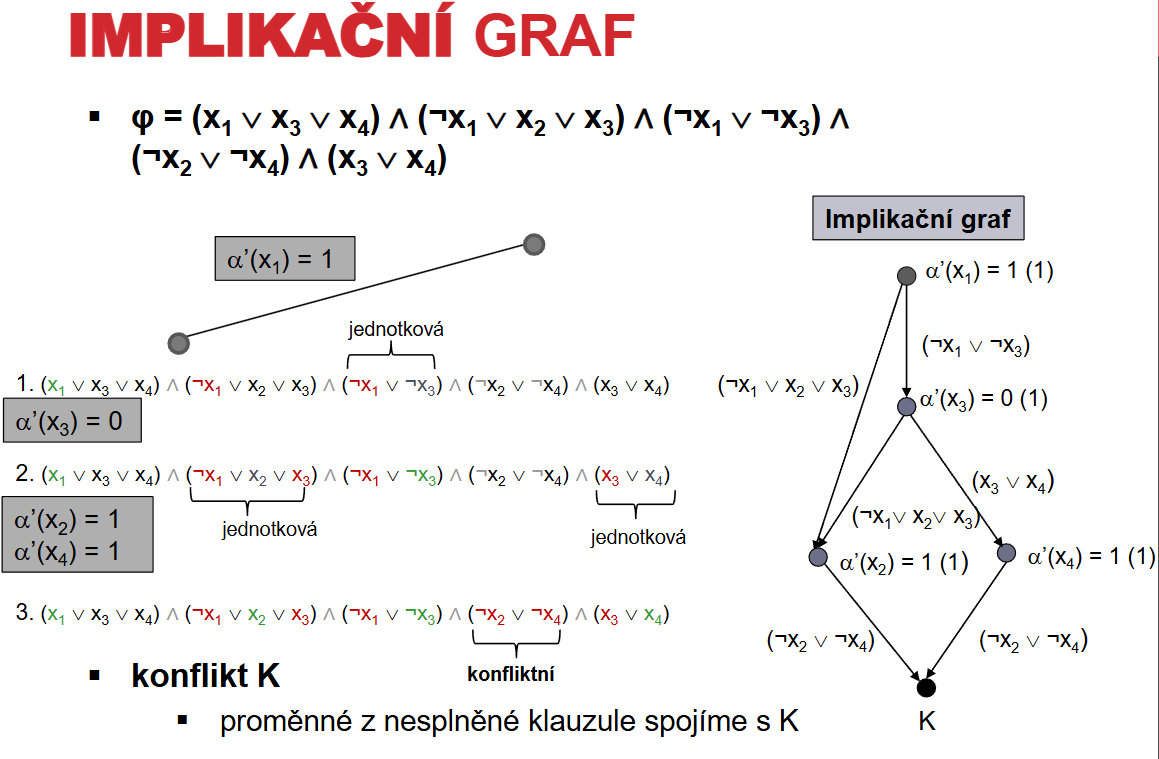
• Příklad:
  • Vybrali jsme ze $\alpha'(x_1)=1$
  • Důsledek toho byl ze jsme ohodnotili $x_1$ jsme mohly ohodnotit $\alpha'(x_3)=0$
  • Důsledek toho ze jsme ohodnotili $x_1, x_3$ jsme mohly ohodnotit $<span class="arithmatex"><span class="MathJax_Preview">\alpha'(x_2)=1</span><script type="math/tex">\alpha'(x_2)=1$,,\alpha'(x_4)=1$$
  • Důsledkem předchozích kroku bylo ze jsme potom dostali konflikt: $\neg x_2 \vee \neg x_4$
  • Z těchto kroku pak můžeme zpětně vytvořit implikační graf

Učení klauzulí:

• Z implikačního grafu se určí hranový řez oddělující $K$ a rozhodovací vrcholy
• Řez definuje konfliktní klauzuli $c$, která je:
  • Logickým důsledkem původní formule ($\phi \Rightarrow c$)
  • Speciálním případem nogoodu
• Naučená klauzule:
  • Zabraňuje opakovanému prohledávání stejného prostoru
  • Určuje úroveň pro zpětný skok (backjump)
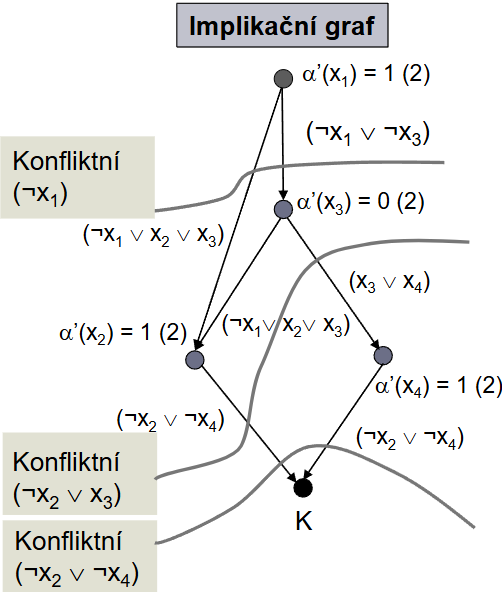
• Příklad:
  • Navazovaní na předchozí příklad ted můžeme udělat rezy v implikačním grafu a dostat další klauzule které musí platit
  • Musi platit: $(\neg x_1)\wedge(\neg x_2 \vee x_3)\wedge(\neg x_2 \vee \neg x_4)$
  • Můžeme se tedy vrátit úplně na začátek a přehodnotit $x_1$

Algoritmus:

1. Jednotková propagace s využitím sledovacích literálů
2. Při konfliktu:
   • Vytvoření implikačního grafu
   • Analýza konfliktu a vytvoření nové klauzule
   • Nechronologický návrat na úroveň určenou konfliktní klauzulí
3. Pokračování v prohledávání s využitím naučených klauzulí

Vlastnosti:

• Algoritmus vždy skončí díky uspořádání na částečných ohodnoceních
• Konfliktní klauzule lze zapomínat po jejich použití pro vynucení

• Implikační graf není třeba explicitně konstruovat:

  • Stačí znát předchůdcovské klauzule
  • Pohyb hranového řezu se simuluje rezolucí

WalkSAT

Lokální prohledávací algoritmus pro řešení SAT problému, který na rozdíl od systematických metod (DPLL, CDCL) používá náhodné procházení stavového prostoru.

Algoritmus:

1. Vytvoř náhodné počáteční ohodnocení
2. Dokud existují nesplněné klauzule:
3. Vyber náhodně nesplněnou klauzuli $c$
4. Proveď jeden ze dvou kroků:
   • Náhodný krok (s pravděpodobností $p$):
     • Náhodně vyber proměnnou z klauzule $c$
     • Změň její hodnotu na opačnou
   • Hladový (greedy) krok (s pravděpodobností $1-p$):
     • Pro každou proměnnou v $c$ spočítej:
       • break count: počet splněných klauzulí, které by se staly nesplněnými
       • make count: počet nesplněných klauzulí, které by se staly splněnými
     • Vyber proměnnou s nejlepším poměrem make/break
     • Změň její hodnotu na opačnou
5. Pokud počet iterací překročí limit, restartuj s novým náhodným ohodnocením

Vlastnosti:

• Náhodný krok pomáhá uniknout z lokálních minim
• Hladový krok směřuje k lepším řešením
• Pravděpodobnost $p$ typicky 0.5
• Restart zabraňuje uvíznutí v těžko řešitelných oblastech

Výhody a nevýhody zůstávají stejné jako v předchozí verzi.

Algoritmy posílání zpráv (Message Passing)

Alternativní přístup k řešení SAT problému, který místo systematického prohledávání používá iterativní výměnu zpráv mezi proměnnými a klauzulemi.

Princip fungování

1. Faktorový graf:
2. Vytvoří se bipartitní graf reprezentující vztahy mezi proměnnými a klauzulemi
3. Vrcholy jsou proměnné a klauzule

4. Hrany spojují proměnné s klauzulemi, ve kterých se vyskytují

5. Výměna zpráv:

6. Klauzule posílají "výstrahy" proměnným
7. Výstraha říká, jakou hodnotu by proměnná měla nabýt pro splnění klauzule

8. Proměnné agregují přijaté zprávy a aktualizují své hodnoty

9. Decimace:

10. Postupné zjednodušování formule přiřazováním hodnot proměnným
11. Hodnoty se vybírají podle agregovaných zpráv
12. Po každém přiřazení se formule zjednoduší

Vlastnosti

Výhody:

• Velmi efektivní na náhodných SAT instancích
• Dobře funguje v oblasti fázového přechodu (nejsložitější instance)
• Paralelizovatelný přístup
• Nízká paměťová náročnost

Nevýhody:

• Není garantována konvergence
• Nemusí najít řešení, i když existuje
• Méně účinný na strukturovaných problémech
• Obtížné teoretické pochopení a analýza

Použití

• Nejúčinnější pro řešení náhodných k-SAT problémů
• Často kombinován s jinými metodami (CDCL, WalkSAT)
• Vhodný pro velké instance v oblasti fázového přechodu
• Používá se jako součást hybridních řešičů
• V oblasti fázového přechodu (kde je SAT nejsložitější) Algoritmy posílání zpráv jsou zde často nejefektivnější

Automatické uvažování

Automatické uvažování (Automated Reasoning) je oblast umělé inteligence, která se zabývá vývojem algoritmů pro automatické dokazování matematických tvrzení a logické odvozování. Zahrnuje několik klíčových oblastí:

Hlavní oblasti:

• Automatické dokazování vět (ATP)

  • Algoritmy pro dokazování, že tvrzení je logickým důsledkem daných axiomů
  • Vyžaduje formalizaci axiomů a tvrzení
  • Plně automatický přístup

• Automatické ověřování důkazů (APC)

  • Interaktivní verze ATP
  • Uživatel zadává důkazové kroky
  • Systém verifikuje jejich správnost

Praktické využití:

• Verifikace hardwaru a softwaru
• Dokazování matematických tvrzení
• Ověřování bezpečnostních vlastností systémů
• Formální verifikace v letectví a kosmonautice

Rozhodování v teoriích prvního řádu

Logika prvního řádu

Základní komponenty:

• Jazyk:
  • Proměnné: $x,y,z,...$
  • Spojky: $\neg, \wedge, \vee, \Rightarrow, \Leftrightarrow$
  • Kvantifikátory: $\forall, \exists$
  • Pomocné symboly: závorky, tečka
• Signatura (nelogické symboly):
  • Funkční symboly: $f,g,h,+,*,...$
  • Predikátové symboly: $R,S,<,=,...$

Struktura formule:

• Term:
  • Proměnná nebo
  • Funkce aplikovaná na termy
• Atom:
  • Predikátový symbol aplikovaný na termy
• Formule:
  • Atom nebo
  • Formule spojená spojkami či s kvantifikátory

Teorie a pravdivost:

• Teorie: množina formulí (i nekonečná)
• Důkaz formule $\phi$ z teorie $T$: posloupnost formulí končící $\phi$
• Struktura: realizace funkcí a predikátů nad modelem
• Model: struktura splňující formule teorie

Obecná rezoluce

Příprava formule:

1. Převod do CNF:
   • Eliminace spojek kromě $\neg, \wedge, \vee$
   • Negace k literálům
     • Vnější negace zpropagujeme dovnitř až k literálům
2. Standardizace proměnných
3. Skolemizace:
   • Náhrada existenčních kvantifikátorů za nove konstanty
   • $\exists x(P(x))$ → $P(A)$, kde $A$ je nová konstanta
   • Použití Skolemových funkcí pro závislosti
4. Odstranění všeobecných kvantifikátorů: $\forall$
5. Distribuce $\vee$ přes $\wedge$

Rezoluční metoda:

• Dostaneme teorii $T'$ ve tvaru CNF a formuli $C'$ jako CNF, jejíž platnost chceme vzhledem k $T'$ ověřovat
  • Sjednocení teorie s negací tvrzení: $T' \cup \neg C' \rightarrow \{T_1 \wedge T_2 \wedge ... \wedge T_n \wedge \neg C'\}$
• Odvození sporu pomocí rezolučního pravidla
  • Tedy postupně slučujeme pravidla tak ze dostaneme prázdnou množinu pravidel
• ANL loop pro systematické prohledávání
• Rezoluce ma své meze:
  • Holičův paradox: Zacykli se
  • Nekonečné teorie

SAT-modulované teorie (SMT)

Princip:

• Kombinuje sílu SAT solverů s teorií prvního řádu
• Umožňuje řešit komplexní logické problémy s teorií (aritmetika, pole, atd.)

Hlavní komponenty:

1. SAT solver:

   • Řeší Booleovskou strukturu formule
   • Vybírá literály pro splnění
   • Pracuje s výrokovou kostrou (propositional skeleton)
   • Nerozumí sémantice teorie

2. DECIDE_T (rozhodovací procedura):

   • Kontroluje splnitelnost v konkrétní teorii
   • Pracuje pouze s konjunkcemi literálů
   • Generuje konfliktní klauzule při nesplnitelnosti
   • Může pracovat s různými teoriemi (aritmetika, rovnost, atd.)

Líný přístup (Lazy Approach):

1. SAT solver navrhne řešení
2. DECIDE_T ověří konzistenci
3. Při konfliktu:
   • Generuje se konfliktní klauzule
   • Přidá se do SAT solveru
   • Proces se opakuje

Zpracování přirozeného jazyka

Základní koncept:

• NLP (Natural Language Processing) umožňuje komunikaci mezi agenty (roboty a lidmi)
• Slouží k nalezení shody na plánech v multiagentním světě

Formální popis jazyka

• Formální jazyk: množina řetězců (konečná i nekonečná)
• Gramatika $G = (N, T, S, P)$:
  • $N$ - konečná množina neterminálů
  • $T$ - konečná množina terminálů
  • $S \in N$ - počáteční neterminál
  • $P$ - konečná množina odvozovacích pravidel

Chomského hierarchie:

1. Rekurzivně spočetné: bez omezení
2. Kontextové: $\alpha X \beta \rightarrow \alpha w \beta$, kde $w$ je neprázdný
3. Bezkontextové: $X \rightarrow w$
4. Regulární: $X \rightarrow x$ nebo $X \rightarrow xY$

Fáze komunikace

1. Záměr sdělit skutečnost
2. Generování sdělení → věta
3. Syntéza → zvuk
4. Vnímání → věta
5. Analýza → derivační strom
6. Odstranění dvojsmyslů
7. Začlenění informace

Pravděpodobnostní přístup

PCFG (Probabilistic Context-Free Grammar):

• Bezkontextová gramatika s pravděpodobnostmi pravidel
• Každé odvození má svou pravděpodobnost
• Učení z korpusu korektních derivačních stromů
• CYK algoritmus: parsování v Chomského normální formě
  • Pravidla tvaru $X \rightarrow YZ$ nebo $X \rightarrow w$

Lexikalizované PCFG:

• Pravděpodobnost závisí na vztahu slov v derivačním stromu
• Využívá nejvýznamnější slovo ve spojení (hlava)

Pokročilé koncepty

DCG (Definite Clause Grammars):

• Gramatiky s podmínkami
• Řeší skloňování a pády
• Příklad: Compatible("black", "dog") vs. Compatible("black", "sugar")

Sémantická analýza:

• Interpretace významu věty
• Využití lambda notace
• Řešení kvantifikace (např. "Every agent feels a breeze")

Strojový překlad

• Statistický přístup
• Rozdělení textu na slovní spojení
• Hledání odpovídajících spojení v cílovém jazyce
• Učení pravděpodobností z korpusu bez derivačních stromů